【無相関の検定】棄却有無の境界線を出してみた

はじめに

統計の勉強で様々な計算式を覚えていく過程で、無相関の検定がなかなか覚えられないので、式を睨んでいました。
そして、気になることがあったので、Pythonで計算させて結果を描画してみました。

• 環境
  • Windows-10-10.0.18362-SP0
  • Python 3.7.6
  • pip 19.3.1
  • pandas 1.0.3
  • matplotlib 3.1.2
  • seaborn 0.10.0
  • numpy 1.18.1
  • scipy 1.4.1

無相関の検定

標本から得られた相関係数から「母集団にも同様の相関がある」と言えるかどうかを検定するもの。

• 帰無仮説H0 : 母相関係数は0である (同様の相関はない)

• 対立仮説H1 : 母相関係数は0ではない

下記の式から、統計量$t$を求め、$p$値を出します。統計量$t$に対する自由度$ν$は$n-2$です。

t = \frac{|r| \sqrt{n - 2}}{\sqrt{1 - r^2}}

有意水準$a$を0.05とした場合は、両側検定で、$p$値0.025点を見れば良いことになります。

... なかなか使わないこともあって、この式が覚えられないんですよ。 ただ、「これってn(サンプルサイズ)が大きければt値大きくなるじゃん、**結局はサンプルサイズじゃん！！**」と思ったので、サンプルサイズと相関係数を総当りさせて、**どのあたりまでなら帰無仮説が棄却されないのか**を見てみました。

準備

#データづくりに使用
import pandas as pd
import numpy as np
import math
from scipy import stats
import itertools

#グラフ描画に使用
import matplotlib.pyplot as plt
import seaborn as sns
from mpl_toolkits.mplot3d import Axes3D


%matplotlib inline


plt.style.use('seaborn-darkgrid')
plt.rcParams['font.family'] = 'Yu Gothic'
plt.rcParams['font.size'] = 20


#相関係数(coef)とサンプルサイズ(n)を入れたら、t値(t)、自由度(df)、p値(p)が返る関数を作成。
def Uncorrelated(coef, n):
    t = (np.abs(coef) * math.sqrt( (n - 2) ) ) / (math.sqrt( ( 1 - (coef**2) ) ) )
    df = (n - 2)
    p = np.round(( 1 - stats.t.cdf(np.abs(t), df) ), 3) #p値丸めてます。
    return coef, n, t, df, p


#サンプル数 10から1000まで10刻み
samplesizes = np.arange(10, 1001, 10)

#相関係数 -0.99から0.99まで0.01刻み
coefficients = np.linspace(-0.99, 0.99, 199)
#print(coefficients)

#上の2つをCrossjoin(直積)
c_s = list(itertools.product(coefficients, samplesizes) )

#相関係数とサンプルサイズを格納したリストをUncorrelated関数へ入れ、帰ってきたものをPandasでDataFrame化
df_prelist = []
for i in range(len(c_s)): 
    df_prelist.append(Uncorrelated(c_s[i][0],c_s[i][1])) 

#準備は完成
df = pd.DataFrame(df_prelist,columns=['coef','sample_size','t','df','p_value'])

dfはこんなかんじ

df

df.sample(10)

相関係数-0.99~0.99,サンプルサイズ10~1000までに対しての無相関の検定のt値、自由度、p値が入っています。

グラフ描画

fig = plt.figure( figsize=(16, 12) )
ax = Axes3D(fig)
cm = plt.cm.get_cmap('RdYlBu')
mappable = ax.scatter( np.array(df['coef']), np.array(df['sample_size']), np.array(df['p_value']), c=np.array(df['p_value']), cmap=cm)
fig.colorbar(mappable, ax=ax)
ax.set_xlabel('相関係数', labelpad=15)
ax.set_ylabel('サンプルサイズ', labelpad=15)
ax.set_zlabel('p値', labelpad=15)
plt.savefig('3次元グラフ.png', bbox_inches='tight', pad_inches=0.3)
plt.show()

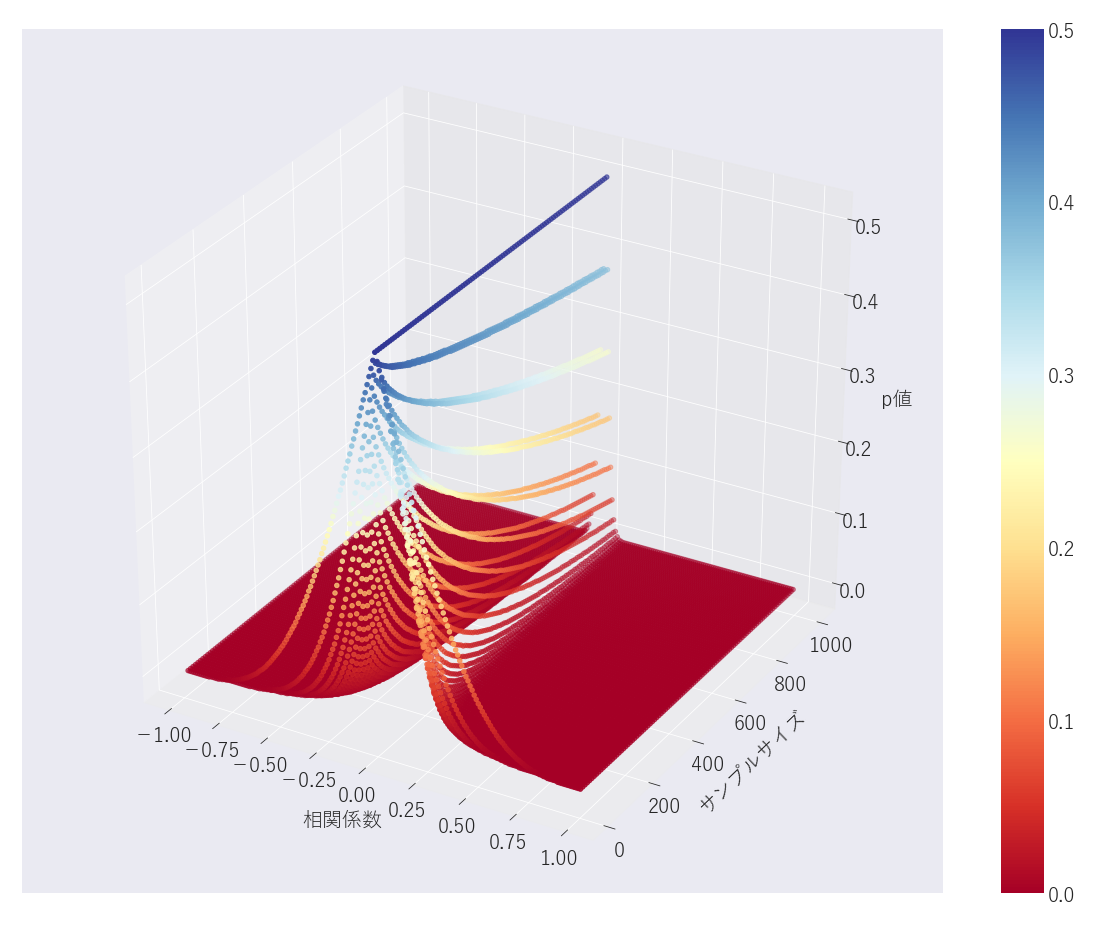
...青色に近づくほど、p値が高く、棄却されないのですが・・・分かりづらいですね

Judgeカラムを作成し、p値が0.025よりも大きいものを、「H0を棄却しない」としてDataFrameを作り直しました。

#p_valueが0.025以上なら、`H0を棄却しない`をつける
df['judge'] = 'H0を棄却する'
for index, series in df.query('p_value > 0.025').iterrows():
    df.at[index, 'judge'] = 'H0を棄却しない'


#グラフ再描画
grid = sns.FacetGrid( df, hue = 'judge', height=10 )
grid.map(plt.scatter, 'coef', 'sample_size')
grid.add_legend(title='判定')
plt.ylabel('サンプルサイズ')
plt.xlabel('相関係数')
plt.title('相関係数xサンプルサイズ 無相関検定の棄却有無', size=30)

#赤線を引く
plt.vlines(df[df['judge'] == 'H0を棄却しない']['coef'].max(), -50, 50, color='red', linestyles='dashed')
plt.vlines(df[df['judge'] == 'H0を棄却しない']['coef'].min(), -50, 50, color='red', linestyles='dashed')
plt.annotate('|' + str(df[df['judge'] == 'H0を棄却しない']['coef'].max().round(2) ) + '|より外側は、n=10以上なら全て棄却する',
            xy=(df[df['judge'] == 'H0を棄却しない']['coef'].max(), 80), size=15, color='black')
plt.savefig('2次元グラフ.png', bbox_inches='tight', pad_inches=0.3)
plt.show()

なるほど、標本の相関係数が絶対値0.62より大きければ、n=10でも帰無仮説H0を棄却して、「母相関係数は0ではない」が採択される($a=0.05$)ということですね！

...ちなみに、「計算式を覚える」という当初の目的はこの記事を書いて覚えました