内容
5段階レビュースコアの得点代表値を出すにあたり、いわゆるベイズ推定を使ってみたくなりました。
ベイズ推定では、設定した分布の計算が煩雑でなければ割と簡単にでき、分布そのものを推定できるという利点があります。
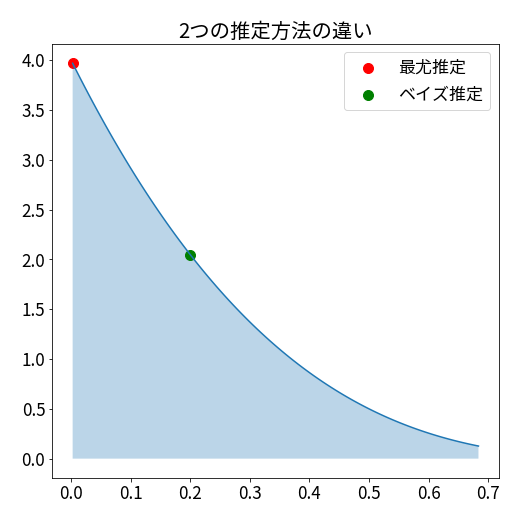
「アプリ内のコインを3回を投げたら表が出た回数は0回だった。このコインの表が出る確率は0%だ!」というのは$0/3 = 0$ いわゆる算術平均で、コインの表が出る確率pを推定しようとなる場合は最尤推定と呼びます。
これに対して、ベイズ推定では表の事象と裏の事象それぞれに数字の<ゲタ>を履かせてあげます。
1のゲタをそれぞれに履かせると$(0 + 1) / (3 + 1 + 1) = 0.2$となります。
ゲタを履かせてあげることをスムージング
1のゲタを履かせてあげることをラプラススムージングともいいます。(解説内容や方向性によっては無情報事前分布ともいいます。)
多段階レビュースコアの点推定をする場合、算術平均とラプラススムージングのベイズ推定どちらが優れているのか気になったので調べてみました。
以降、ラプラススムージングによるベイズ推定を「ラプラススムージング」
スムージングによるベイズ推定を「スムージング」
と記載します。
シミュレーション
最尤推定とベイズ推定
これら2つの推定方法で点推定をするというのは、今回のコインの例だと以下のようなことになります。
最尤推定は分布の一番高い場所を推定値とします。
ベイズ推定は事後分布の期待値を推定値とします。今回の場合はベータ分布の期待値となります。
確率とサンプル数を決めて比較
真の確率$p$を$[0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 1]$
サンプルサイズ$n$を$[3, 5, 10, 30, 50, 100, 500, 1000]$
として、それぞれのパターンをすべて組み合わせて、どちらが真の確率に近いのかを比べてみました。
$n=3, p=0.5$の場合は、表が出る確率が$0.5$のコインを$3$回投げてその成功回数を観測します。
それを10万回行い、10万回それぞれ算術平均とラプラススムージングではどちらが真の確率に近い推定値を出したか比較します。
そして、ラプラススムージングのほうが近い推定値を出した場合は「1」を、算術平均のほうが近い推定値を出した場合は「0」をカウントして勝率を見ます。
その次に$n=5, p=0.5$は・・・のようにすべてのパターンを繰り返していきます。
def estimate_simulate(n, p):
# 成功回数
x = binom.rvs(n, p, size=100000)
# 最尤推定
maximum_likelihood = x / n
# ベイズ推定
bayes = (x + 1) / (n + 2)
# 真の確率との差を比較
estimate_diff_ml = np.abs(maximum_likelihood - p)
estimate_diff_b = np.abs(bayes - p)
# ベイズ推定のほうが真の確率との誤差が小さい場合1を返す
result = np.int64(estimate_diff_b < estimate_diff_ml)
# DataFrameを返す
return pd.DataFrame({
'n': n,
'p' : p,
'ml_estimate' : maximum_likelihood,
'b_estimate' : bayes,
'ml_diff' : estimate_diff_ml,
'b_diff' : estimate_diff_b,
'result' : result
})
dfs = []
for v in list(product(n, p)):
dfs.append(estimate_simulate(v[0], v[1]))
df = pd.concat(dfs)
確率毎の勝率
確率毎の勝率では、真の確率pが0.5に近いほどラムラススムージングのほうが良い結果となりました。
| 真の確率p | 勝率 |
|---|---|
| 0.5 | 91.96% |
| 0.6 | 58.58% |
| 0.7 | 49.98% |
| 0.8 | 46.11% |
| 0.9 | 40.39% |
| 0.95 | 38.62% |
| 1 | 0.00% |
これは、ラプラススムージングの別名として無情報事前分布というのを出しましたが、これが関係していると思います。
ラプラススムージングは確率0~1まで一様な確率である事前分布を設定します。
そのため、$[0,1]$の一様分布の期待値である$0.5$が真の確率であるときが良い推定値となりやすいです。
確率 x サンプルサイズ毎の勝率
56パターンがあるため、特徴的な部分だけを取り出してみました。
p = 0.5
真の確率$p = 0.5$の場合、すべてのサンプルサイズにおいて算術平均よりも良い点推定ができています。
| 真の確率p | サンプルサイズ | 勝率 |
|---|---|---|
| 0.5 | 3 | 100.00% |
| 0.5 | 5 | 100.00% |
| 0.5 | 10 | 75.40% |
| 0.5 | 30 | 85.55% |
| 0.5 | 50 | 88.75% |
| 0.5 | 100 | 92.05% |
| 0.5 | 500 | 96.44% |
| 0.5 | 1000 | 97.48% |
p = 0.5 ~ 0.7
真の確率$p$が1へ近づいていくと、サンプルサイズの増加とともに勝率が下がっています。
| 真の確率p | サンプルサイズ | 勝率 |
|---|---|---|
| 0.5 | 3 | 100.00% |
| 0.5 | 5 | 100.00% |
| 0.5 | 10 | 75.40% |
| 0.6 | 3 | 100.00% |
| 0.6 | 5 | 65.33% |
| 0.6 | 10 | 54.98% |
| 0.7 | 3 | 55.84% |
| 0.7 | 5 | 69.27% |
| 0.7 | 10 | 43.05% |
p = 0.95
真の確率p = 0.95$の場合、サンプルサイズ10~50の場合に勝率が50%より高い結果となりました。
| 真の確率p | サンプルサイズ | 勝率 |
|---|---|---|
| 0.95 | 3 | 0.74% |
| 0.95 | 5 | 0.12% |
| 0.95 | 10 | 59.83% |
| 0.95 | 30 | 55.54% |
| 0.95 | 50 | 53.96% |
| 0.95 | 100 | 43.53% |
| 0.95 | 500 | 47.13% |
| 0.95 | 1000 | 48.08% |
p = 1
真の確率$p = 1$の場合、分布を推定するベイズ推定の場合期待値がピッタリ1である確率は0のため、勝つことはないです。
| 真の確率p | サンプルサイズ | 勝率 |
|---|---|---|
| 1 | 3 | 0.00% |
| 1 | 5 | 0.00% |
| 1 | 10 | 0.00% |
| 1 | 30 | 0.00% |
| 1 | 50 | 0.00% |
| 1 | 100 | 0.00% |
| 1 | 500 | 0.00% |
| 1 | 1000 | 0.00% |
真の確率pをランダムにして比較
0.5の場合勝ちやすい 1に近い場合負けやすい みたいなのはわかりましたが、汎化性能がどうなのか気になりました。
確率pを0~1の間でランダムに生成させることにして、サンプルサイズだけ$[3, 5, 10, 30, 50, 100, 500, 1000]$のパターンで検証してみました。
def estimate_simulate_prand(n):
# pをランダムに決定する
p = np.random.random(size=100000)
# 成功回数
x = binom.rvs(n, p)
# 最尤推定
maximum_likelihood = x / n
# ベイズ推定
bayes = (x + 1) / (n + 2)
# 真の確率との差を比較
estimate_diff_ml = np.abs(maximum_likelihood - p)
estimate_diff_b = np.abs(bayes - p)
# ベイズ推定のほうが真の確率との誤差が小さい場合1を返す
result = np.int64(estimate_diff_b < estimate_diff_ml)
# DataFrameを返す
return pd.DataFrame({
'n': n,
'p' : p,
'ml_estimate' : maximum_likelihood,
'b_estimate' : bayes,
'ml_diff' : estimate_diff_ml,
'b_diff' : estimate_diff_b,
'result' : result
})
dfs = []
for v in n:
dfs.append(estimate_simulate_prand(v))
df1 = pd.concat(dfs)
勝率
サンプルサイズ$n$を問わず勝率の平均を出したところ、52.51%でした。僅かにラプラススムージングのほうが良い結果となりました。
サンプルサイズ毎の勝率
全てのサンプルサイズでラプラススムージングのほうが勝率が高くなりました。
特にn=3, 5での勝率が高いです。
| サンプルサイズ | 勝率 |
|---|---|
| 3 | 59.42% |
| 5 | 56.85% |
| 10 | 50.10% |
| 30 | 51.00% |
| 50 | 51.00% |
| 100 | 50.86% |
| 500 | 50.62% |
| 1000 | 50.23% |
落とし穴
真の確率pをランダムで出力した場合、ラプラススムージングのほうが確率の点推定においてよい結果になりましたが、現実の分析で真の確率pがランダムに降ってくることがまずあり得ないです。
- 例(値は適当です)
- 広告のCTRはだいたい0.2%
- 商品Aのバスケット購入率は大体0.1%
- 天気予報の的中率は大体87%
これらの分析を中心に行っている場合、分析対象である事象の真の確率pが0~1間でランダムに発生することはまずないと思います。
これについてはスムージングの値を変更することによって対応することができるので、後ほど比較しています。
多段階レビューで比較
上記までの例では裏 or 表の2項の場合でしたが、多項の場合はどうなるか検証しました。
多項の場合のラプラススムージングは、項の数だけ1のゲタを履かせてあげます。
項を5段階として考えます。
そして、それぞれの項の誤差を2乗したものを5で割り、1/2乗します(RMSE)
5項それぞれの確率$p$はランダムに出力します。
サンプルサイズ$n$は$[3, 5, 10, 30, 50, 100, 500, 1000, 10000]$を用います。
def estimate_simulate_prand_multi(n):
# 5項の確率pをランダムに出力する(この後の計算で、p_の総和が1を超える時がありエラーを吐くため、試行回数は1000回に抑える)
p = dirichlet.rvs(np.repeat(0.2, 5), size=1000)
# それぞれの採択回数
x = np.array([multinomial.rvs(n, p_) for p_ in p])
# 最尤推定
maximum_likelihood = x / n
# ベイズ推定
bayes = (x + np.ones(5)) / (n + 5)
# 真のpとの差を比較
estimate_diff_ml = np.sqrt(np.sum(np.square(maximum_likelihood - p), axis=1) / 5)
estimate_diff_b = np.sqrt(np.sum(np.square(bayes - p), axis=1) / 5)
# ベイズ推定のほうが真の確率との誤差が小さい場合1を返す
result = np.int64(estimate_diff_b < estimate_diff_ml)
# DataFrameを返す
return pd.DataFrame({
'n' : n,
'ml_diff' : estimate_diff_ml,
'b_diff' : estimate_diff_b,
'result' : result
})
dfs = []
for v in n:
dfs.append(estimate_simulate_prand_multi(v))
df2 = pd.concat(dfs)
勝率
サンプルサイズ$n$を問わず勝率の平均を出したところ、36.86%でした。算術平均のほうが良い結果となりました。
サンプルサイズ毎の勝率
全てのサンプルサイズで算術平均のほうが勝率が高くなりました。
多項の場合、それぞれの確率pを求めるのにラプラススムージングはあまり効果がないかもしれません。
| サンプルサイズ | 勝率 |
|---|---|
| 3 | 34.20% |
| 5 | 34.10% |
| 10 | 29.80% |
| 30 | 29.30% |
| 50 | 34.70% |
| 100 | 37.80% |
| 500 | 41.30% |
| 1000 | 43.30% |
| 10000 | 47.20% |
スムージングのパラメータを推定して比較
ラプラススムージングは各項に1のゲタを履かせますが、スムージングは任意の値のゲタを履かせることができます。
落とし穴で説明したように、基本的に分析対象の真の確率pは「だいたいこれくらいではあるでしょ」なぼんやりしたものがあると思います。
それをスムージングのパラメータに反映させたいです。
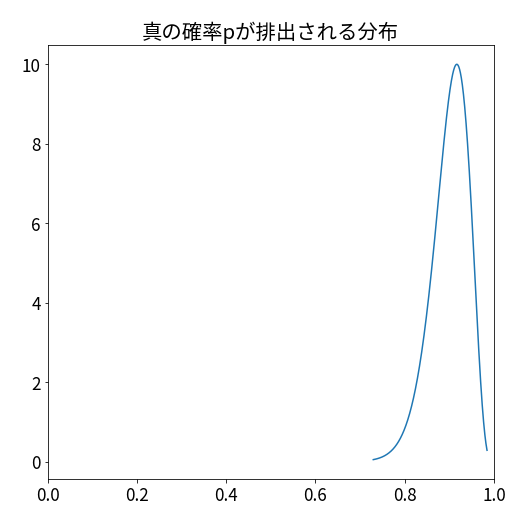
真の確率pの分布
真の確率pがランダムに排出される分布を以下とします。
上記はベータ分布(45, 5)であり、だいたい0.8 ~ 1の値が排出されます。
スムージングパラメータ推定
スムージングのパラメータを推定する以下の関数を適用しその値をスムージングの値とします。
from scipy.special import psi
def new_hyperprior(x, a, b, loop=1000):
for l in range(loop):
a_t__a_b = 0
a_b = 0
b_t__a_b = 0
for (i, c) in x:
if c != 0:
a_t__a_b += psi(c+a) - psi(a)
a_b_ = psi(i+a+b) - psi(a+b)
a_b += a_b_
a_t__a_b -= a_b_
b_t__a_b += psi(i-c+b) - psi(b)
b_t__a_b -= a_b_
a_r = a_t__a_b / a_b
a = a_r * a + a
b_r = b_t__a_b / a_b
b = b_r * b + b
if (l % 1000 == 0):
print(f'l:{l}, a:{a: .15f}, b:{b: .15f}')
# if (np.abs(a_r) < EPSILON) & (np.abs(b_r) < EPSILON): EPSILON変数がどこで作られてるのか不明なためスルー 両方誤差より小さければ実行を打ち止めするものっぽい
# break
print(f'l:{l} a:{a: .15f}, b:{b: .15f}')
これはベルヌーイ分布における超パラメータ推定のための経験ベイズ法のJuliaで書かれたコードをPython3に書き直したものです。
new_hyperprior関数に入れる$x$は$(試行回数 , 成功回数)$のタプルとなっています。
ここに上記分布から排出された確率pをもとにした観測結果を入れます。
Beta(45,5)の確率分布から排出されるpをもとに過去サンプルサイズを100として分析を行ったとして、その結果をxの値とします。
a, b = 45, 5
obs = beta.rvs(a, b, random_state=46)
print(binom.rvs(100, obs, random_state=46))
83
この場合$x = (100, 83)$となります。
new_hyperprior([(100, 83)], 1, 2)
l:999 a: 303.577507284060573, b: 62.575505272794054
成功の項のゲタが303.57.... , 失敗の項のゲタが62.57....となりました。
このパラメータを適用して、ベイズ推定と最尤推定でどちらが真の確率pの点推定に優れているのかを検証します。
def estimate_simulate_betaprand(n, alpha_, beta_):
# 真の成功確率pを上記のベータ分布とする
p = beta.rvs(a=45, b=5, size=100000)
# 成功回数
x = binom.rvs(n, p)
# 最尤推定
maximum_likelihood = x / n
# ベイズ推定
bayes = (x + alpha_) / (n + alpha_ + beta_)
# 真の確率との差を比較
estimate_diff_ml = np.abs(maximum_likelihood - p)
estimate_diff_b = np.abs(bayes - p)
# ベイズ推定のほうが真の確率との誤差が小さい場合1を返す
result = np.int64(estimate_diff_b < estimate_diff_ml)
# DataFrameを返す
return pd.DataFrame({
'n': n,
'p' : p,
'ml_estimate' : maximum_likelihood,
'b_estimate' : bayes,
'ml_diff' : estimate_diff_ml,
'b_diff' : estimate_diff_b,
'result' : result
})
dfs = []
for v in n:
dfs.append(estimate_simulate_betaprand(v, 303.57, 62.57))
df4 = pd.concat(dfs)
勝率
勝率は35.41%でした。算術平均のほうが良い結果となりました。
サンプルサイズ毎の勝率
サンプルサイズが少ないとき、スムージングのほうが良い結果となりますが、大きくなると算術平均のほうが良い結果となりました。
| サンプルサイズ | 勝率 |
|---|---|
| 3 | 66.70% |
| 5 | 69.31% |
| 10 | 48.69% |
| 30 | 26.12% |
| 50 | 23.16% |
| 100 | 17.45% |
| 500 | 14.98% |
| 1000 | 16.86% |
ベイズ推定の何がいいのか
スムージングパラメータの推定を試した時は「流石にベイズ推定のほうが良い結果になるでしょ」と思ってましたが、そうではなかったです。
が、今回の判定方法は「真の確率pについてより近いほうが勝ち」スタイルであり、どれくらい近いのかは説明していないです。
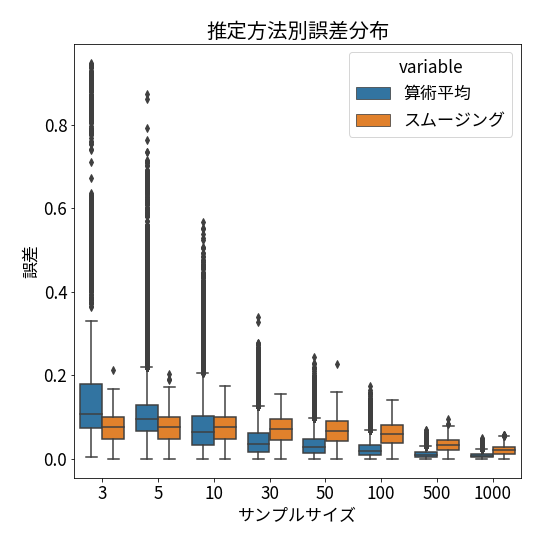
点推定における誤差分布
関数の中身を見るとわかりますが、それぞれの誤差も一緒に出力しているため、誤差の分布をプロットしてみます。
算術平均のほうが大きな誤差を出す場合が多く、箱ひげ図でいう外れ値とされる場合が多々あることが分かります。
スムージングでは、サンプルサイズ100あたりまで誤差の分布がほぼ一定で、それ以降は分布のばらつきも小さくなり始めます。
安定した推定値を出したいのであればスムージング(ベイズ推定)
より良い代表値の点推定をしたいのであれば算術平均
という形かもしれないです。
分布の推定
抑々ベイズ推定は分布そのものを推定する方法なので、結果の解釈がし易いです。
真の確率pの区間推定をする場合、頻度論の統計であれば信頼区間というものが使われます。
今回でいえば「真の確率pの95%信頼区間は87% ~ 93%です」のような形で使われます(値は適当)
この意味は、「真の確率pから標本を取得し、その平均から95%信頼区間を求める、という作業を100回やった時、95回はその区間の中に真の確率pが含まれる」という意味です。
(詳しくは統計WEB : 19-3. 95%信頼区間のもつ意味が図付きで分かりやすいです)
「なんてややこしいんだ」と思います。
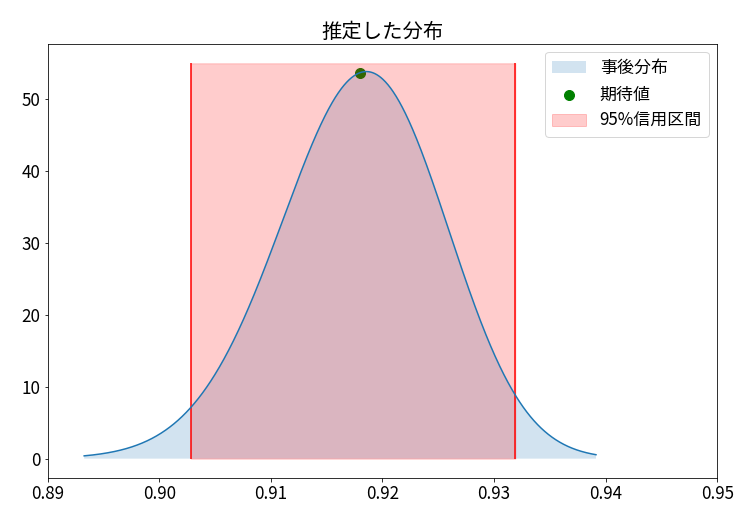
ベイズ推定の場合、真の確率pに対する区間推定は信用区間というものを用います。
95%信用区間というのは以下のようなものになります。
| 期待値 | 2.5%点 | 97.5%点 | |
|---|---|---|---|
| 0.9179... | 0.9028... | 0.9319... |
「真の確率pは95%の確率で0.9028... ~ 0.9319...の間に入っている」
めちゃくちゃわかりやすいと思います。なんなら統計勉強したてなら信頼区間を間違ってこう解釈したりするような・・・
分布そのものを推定するため、このようなわかりやすい解釈ができます。
一方で、分布そのものを推定する時、どうしても微積分の計算が難解になってしまう時があります。
その場合には、マルコフ連鎖モンテカルロ法を用いて分布を探索したりします。
まとめ
自分なりの解釈をまとめたものなので、間違っているかもしれません。その場合はご指摘いただけると助かります。
- 内容のような、簡単な代表値を1つ出す場合、算術平均でいいと思う
- 点推定した値のばらつきが気になるならスムージング(ベイズ推定)
- ある程度のばらつきは理解したうえで、より良い点推定をしたいなら算術平均
- 区間推定の解釈性ならスムージング(ベイズ推定)
- ただし簡単に事後分布が求まらない場合あり