内容
標準正規分布とカイ二乗分布の関係を用いて、ホテリングT2法という簡単な異常検知モデルを作成することができます。
確率変数$X$が標準正規分布$N(0,1)$に従う時、$X^2$は自由度1のカイ二乗分布$\chi^2_1$に従う為、この分布をベースに「異常である」の閾値$a$を設定し、新たに観測した値から導かれる異常度$a(x')$が閾値$a$を超えるなら「異常」とする方法です。

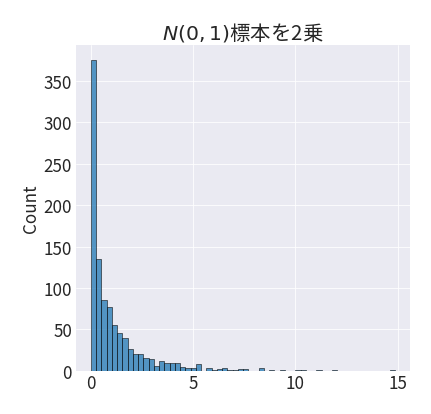
実際に標準正規分布から取得した1000の標本を2乗して、プロットしてみます。
from scipy.stats import norm chi2
import matplotlib.pyplot as plt
import seaborn as sns
# 実際にやってみる
x = norm.rvs(loc=0, scale=1, size=1000, random_state=100)
plt.figure(figsize=(6, 6))
sns.histplot(x)
plt.title('$N(0, 1)$からの標本 (n=1000)')
plt.savefig('正規分布標本.png')
plt.show()
2乗してプロットします。
# 二乗する
x2 = x**2
plt.figure(figsize=(6, 6))
sns.histplot(x2)
plt.title('$N(0, 1)$標本を2乗')
plt.show()
自由度1のカイ二乗分布に従っています(証明はこちら)
実装
先に閾値$a$を決めておきます。今回は自由度1のカイ二乗分布の97.5%点である5.02を閾値$a$とします。
次に、正常な標本がほとんどだと言えるデータから標本平均と標本標準偏差を求めます。
今回は例として、正常な標本が$N(10, 5^2)$に従っているとして、サンプルを取得します。
# 正常時のサンプルを生成する
mu = 10
scale= 5
sample = norm.rvs(loc=mu, scale=scale, size=1000, random_state=46)
# プロット
plt.figure(figsize=(6, 6))
sns.histplot(sample)
plt.title('正常時サンプルのヒストグラム')
plt.show()
標本平均と標本標準偏差を求めます。
# 標本から平均と標準偏差を算出
sample_mu = sample.mean()
sample_sigma = sample.std()
print(sample_mu, sample_sigma)
9.92654000756153 5.092873537096135
新たな観測値を得たら、平均と標準偏差を用いて値を標準化し、標準化した値を2乗して異常度とします。
# 新しく観測したデータ
new_sample = np.array([14, 0, 30])
# 標準化した値を2乗する
standardization_value = ((new_sample - sample_mu) / sample_sigma)
outlier_check_value = standardization_value ** 2
outlier_check_value
array([ 0.63973649, 3.79900627, 15.53526583])
3つの異常度$a(x')$が求まりました。
閾値$a$より大きい、3番目の観測値30を異常とします。
手軽に実装できますが、論理的に予測される値と実際が食い違うことから「異常」とされやすいという欠点もあります。
モーメント法を用いたカイ二乗分布の当て嵌めを行い、自由度を決定する方法もあります。
証明
確率変数$Z$が標準正規分布$N(0,1)$に従う時、$Z^2$が自由度$1$のカイ二乗分布$\chi^2_1$に従うことを証明します。
自由度$n$のカイ二乗分布$\chi^2_n$の確率密度関数は以下の式で与えられます。
f(x) = \frac{1}{\Gamma(n/2)} \Bigl( \frac{1}{2} \Bigr)^{n/2}x^{\frac{n}{2}-1}\exp(-x/2), \quad x > 0
よって、自由度1の場合は、以下となります。
f(x) = \frac{1}{\Gamma(1/2)} \Bigl( \frac{1}{2} \Bigr)^{1/2}x^{-\frac{1}{2}}\exp(-x/2), \quad x > 0
変数変換
$N(0,1)$に従う確率変数の二乗が$\chi^2_1$になるまでの導出について、変数変換を用います。
関数$g(\cdot)$を通して確率変数$X$を$Y = g(X)$に変換したとき、$Y$の分布を$X$の分布から導くことを考えます。
$Y$の累積分布関数$F(y)$は
F(y) = P(Y \leq y)
であり、$Y = g(X)$より
F(y) = P(g(X) \leq y) = P(X \in \{x | g(x) \leq y \})
となり、確率密度関数は累積分布関数の微分で得られることから、
f(y) = \frac{d}{dy}F(y) = \frac{d}{dy}P(X \in \{x | g(x) \leq y \})
と導かれます。
平方変換
確率変数$X$の確率密度関数を$f(x)$としたときの、$X$の平方変換$Y = X^2$について考えます。
変数変換式から、$y > 0$に対して
\{ x | x^2 \leq y \} = \{ x | - \sqrt{y} \leq x \leq \sqrt{y} \}
であるので、確率密度関数$g(y)$は
g(y) = \frac{d}{dy}G(y) = \frac{d}{dy}P(X \in \{ x | - \sqrt{y} \leq x \leq \sqrt{y} \}) \\
= \frac{d}{dy}\int_{-\sqrt{y}}^{\sqrt{y}}f(x) dx \\
= \{ f(\sqrt{y}) + f(-\sqrt{y}) \}\frac{1}{2 \sqrt{y}}
となることから
g(y) = \{ f(\sqrt{y}) + f(-\sqrt{y}) \}\frac{1}{2 \sqrt{y}}
と導かれます。
確率密度関数$f(x)$が$y$軸に対して対称(正規分布等)な場合は$f(-x) = f(x)$となるため、
g(y) = \frac{f(\sqrt{y})}{\sqrt{y}}
とも書けます。
平方変換の適用
確率変数$X$の確率密度関数$f(x)$を$N(0,1)$として変換します。
正規分布$N(\mu, \sigma^2)$の確率密度関数は以下の式で与えられます。
f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}}\exp \biggl(-\frac{(x - \mu)^2}{2\sigma^2} \biggr)
よって、標準正規分布$N(0, 1)$は以下となります。
f(x) = \frac{1}{\sqrt{2 \pi}} \exp \biggl(-\frac{x^2}{2} \biggr)
$X$の平方変換$Y = X^2$の$g(y) = \frac{f(\sqrt{y})}{\sqrt{y}}$を適用すると、
g(y) = \frac{1}{\sqrt{y}}\cdot\frac{1}{\sqrt{2 \pi}} \exp \biggl(-\frac{y}{2} \biggr) \\
= \frac{1}{\sqrt{\pi}} \Bigl( \frac{1}{2}\Bigr)^{1/2} y^{-\frac{1}{2}} \exp (-y/2), \quad y > 0
となります。
ガンマ関数
\frac{1}{\sqrt{\pi}} \Bigl( \frac{1}{2}\Bigr)^{1/2} y^{-\frac{1}{2}} \exp (-y/2)
上式の$\sqrt{\pi}$を$\Gamma{(1/2)}$へ変換します。
ガンマ関数$\Gamma{(x)}$は正の実数$x$に対して、以下の式で与えられます。
\Gamma{(x)} = \int_{0}^{\infty} t^{x-1} e^{-t} dt
$\Gamma{(1/2)}$の場合、$t = u^2$の置換積分を用いて
\Gamma{(1/2)} = \int_{0}^{\infty}t^{-\frac{1}{2}}e^{-t} dt \\
= \int_{0}^{\infty} u^{-1} e^{-u^2}2u du \\
= 2 \int_{0}^{\infty}e^{-u^2}du
となります。
ガウス積分
$\int_{0}^{\infty}e^{-u^2}du$の部分ですが、以下のガウス積分を用いて$\pi$へ変換します。
\int_{-\infty}^{\infty}e^{-u^2}du = \sqrt{\pi}
ガウス積分の証明は、2次元極座標$(\rho, \phi)$を用いて可能です。
ガウス積分の値を$I$と置きます。
I = \int_{-\infty}^{\infty}e^{-x^2}dx \\
これを2乗し$I^2$とします。こちらを解いていきます。
$x = \rho \cos{\phi}, y= \rho \sin{\phi}$と置換し、$\rho = \sqrt{x^2 + y^2}$となる事も用いると、
I^2 = \int_{-\infty}^{\infty}e^{-x^2}dx \int_{-\infty}^{\infty}e^{-y^2}dy \\
= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2 + y^2)}dxdy \\
= \int_{0}^{2\pi} d\phi \int_{0}^{\infty}e^{-\rho^2} \rho d\rho \\
= 2 \pi \int_{0}^{\infty}e^{-\rho^2} \rho d \rho \\
= 2 \pi \biggl[ -\frac{e^{-\rho^2}}{2}\biggr]_{0}^{\infty} \\
= \pi
となりますので、
I = \int_{-\infty}^{\infty}e^{-x^2}dx = \sqrt{\pi}
よって、
\Gamma{(1/2)} = 2 \int_{0}^{\infty}e^{-u^2}du = 2 \cdot \frac{\sqrt{\pi}}{2} = \sqrt{\pi}
となるため、$\sqrt{\pi}$は$\Gamma{(1/2)}$へ変換でき、
\frac{1}{\Gamma{(1/2)}} \Bigl( \frac{1}{2}\Bigr)^{1/2} y^{-\frac{1}{2}} \exp (-y/2), \quad y > 0
となります。
平方変換を用いて、標準正規分布$N(0,1)$に従う確率変数の二乗が自由度11のカイ二乗分布$\chi^2_1$になる事が証明できました。