施策がもたらす主要指標への影響をPyMCで推定してみる

内容

特定の施策による主要指標(KPI等)への影響を知りたい場合があります。
また、事業関連の場合そのデータは往々にして時系列データであることが多いです。

• 例
  • SNSによる投稿Aが売上に与える影響を知りたい
  • 広告Aが売上に与える影響を知りたい
  • 投稿動画Aが売上に与える影響を知りたい

このような場合の影響をPyMCライブラリを用いて推定してみました。

動作環境

• Windows 11 (WSL2 Ubuntu 20.04)
• Python 3.11.4
• PyMC 5.21.1

実際に動かしているリポジトリは以下になります。uvを使って環境を構築しています。

データ例

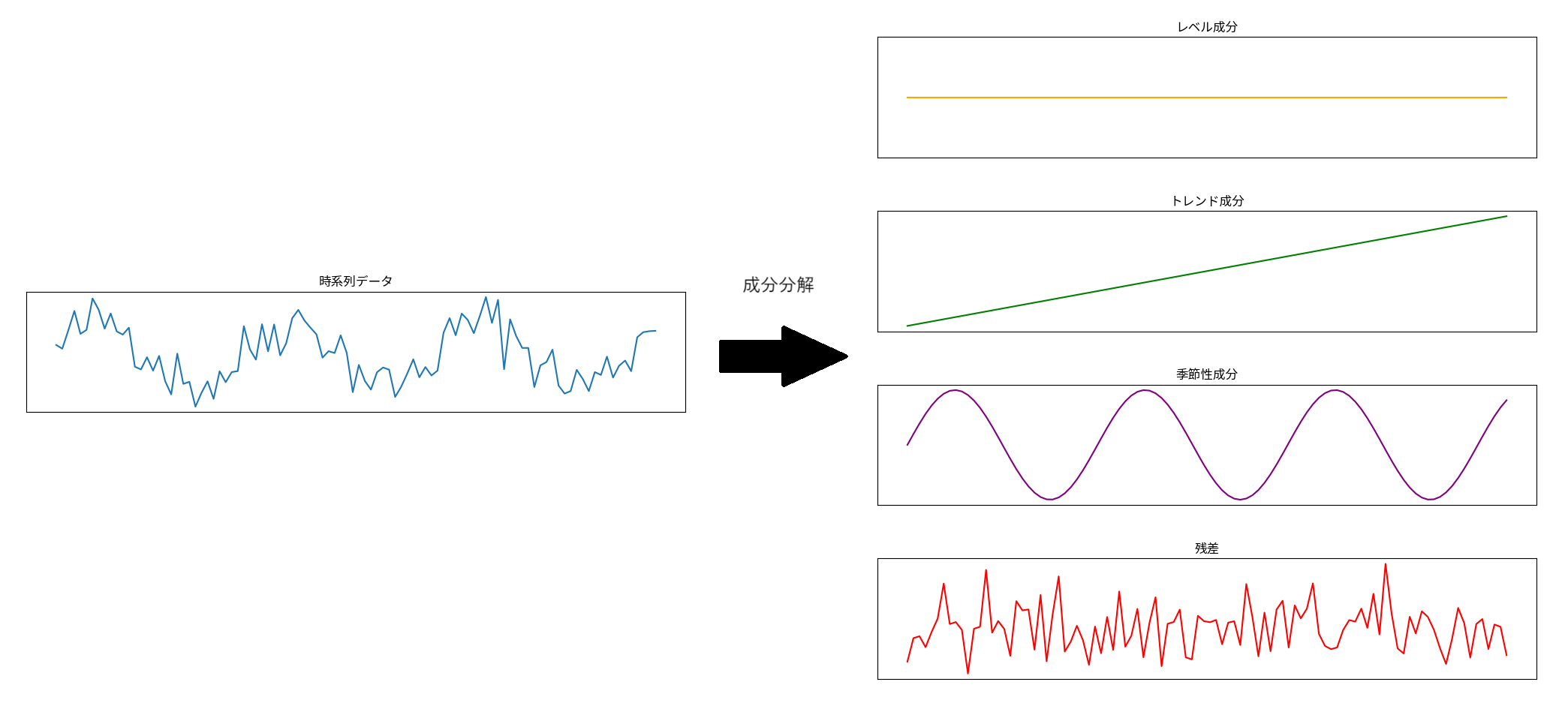
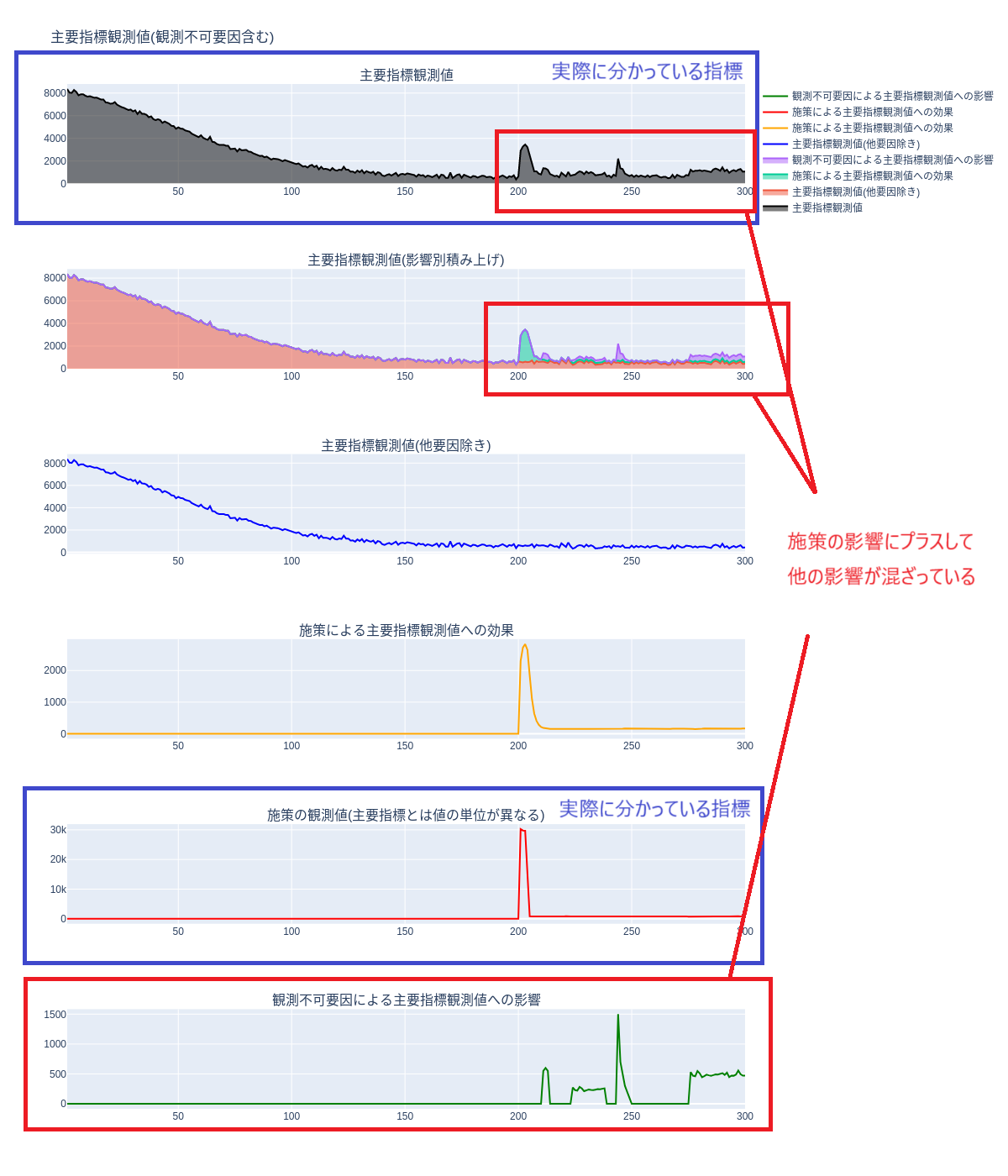
内容の具体的なシチュエーションを図にすると上記のようになると思います。

流れとしては、

1. 施策について施策の単位での数字が分かる(一番下の図)
2. 主要指標について数字が分かる(一番上の図)
3. 施策が与えた主要指標への影響が分からない(真ん中3つの図)
4. 推定しよう

な感じです。

PyMC選定理由

その前に、今回のシチュエーションに於いてPyMCを使う理由をざっくりと記載しようと思います。

PyMCは確率分布を使ってパラメータ間の関係性を記述したモデルを定義し、マルコフ連鎖モンテカルロ法(MCMC)によるベイズ推論を行うことができるライブラリです。

トレンド・季節性成分分解モデル

時系列分析の場合、まず手法として挙げられるのが、$y$を

$$
\hat{y} = level + trend + season + \epsilon
$$

• レベル成分
• 傾き成分
• 周期性成分

の3つの成分に分解したモデルです。（下図はイメージ）

ライブラリではprophet,statsmodelsがあります。

この時系列モデルについては$\hat{y}$の予測を行うのには使えるのですが、今回のように施策による主要指標への影響

$$
\hat{y} = \beta x + \epsilon
$$

の$\beta$部分を推定したい場合には適していません。
このモデルについては、yの予測を目的としており施策の観測値を入力として持っていない為です。

線形・ガウス型状態空間モデル

では、

$$
\hat{y} = \beta x + \epsilon
$$

でモデル化するのが良いと考えられます。
が、今回の観測値は時系列データであり、時系列の要素を取り入れたいです。

状態空間モデルは、時系列のような互いに関連のある系列的なデータを確率的にとらえるモデルの一つで、時系列要素を取り入れられます。

このモデルは、状態方程式・観測方程式を用いて、観測値を「特定の分布から得られた1サンプル」と捉えるモデルです。
また、時系列による状態更新はベイズ推定を用いています。時系列データが、先頭から終わりまでを$1,2...,T$とすると、$t=0$の部分に対して事前分布を設定し、そこから時系列順に状態を更新していきます。

$t=0$から$t=1$の動きについては、事前分布に$t=1$で得られた観測値(に基づく尤度)をかけます。

$t=1$以降におけるベイズ更新は

$$
p(x_1 | y_1) \propto p(x_1) \times p(y_1 | x_1)
$$

式により更新します。

上記計算において、$x$(状態)が従うと仮定した分布が計算可能な場合、$1,2...T$まで逐次的に状態を更新することができます。

仮定した分布が計算可能

線形かつ正規分布に従うと仮定した場合、カルマンフィルタが挙げられます。
その他共役事前分布を活用したモデルもあります。(詳しくは8基礎からわかる時系列分析 --Rで実践するカルマンフィルタ・MCMC・粒子フィルターの5章以降が分かりやすいです。)

つまり、今回の内容において計算可能であればベイズ更新におけるモデルを作れそうです。

結論からいうと、今回行う主要指標への影響推定では難しいです。

理由としては、施策の観測値$x$について、MMM(マーケティング・ミックス・モデル）でも採用されている「残存効果」「飽和効果」を導入し、これが非線形となる為です。

その他定義するモデルによっては計算不可能となる場合は、
今回のようにMCMC（マルコフ連鎖モンテカルロ法）を用いた近似解による推定を行う形になります。

PyMCによる推定

こちらの図の大元となっているデータを生成してPyMCによる推定を行います。

データセット

こちらのスクリプトを実行して生成します。

$ uv run python3 create_data.py

長さが300、主要指標についてはリリース時にピークを迎え、減衰していくものを仮定しています。（楽曲の視聴回数、新商品の販売数等）

そこに、施策の観測値と、施策の観測値あたりの効果係数を設定します。

create_data.py 一部抜粋

    MEM = MediaEffectModel()
    MS = MetricScaler()
    T = 300 # サンプルの長さ
    tl = np.arange(1, T+1)
    t = np.linspace(0, 1, T)
    mu_start = 10000; mu_end = 500

    # 減衰具合を調整
    k = 10 # 傾き
    t0 = 0.15 # 勾配が変化する点
    s = 1 / (1 + np.exp(-k * (t - t0))) # ロジスティック関数で0~1の値を生成
    mu = mu_end + (mu_start - mu_end) * (1 - s) # 逆数をとってmuとする
    var = 10000

    # mu, varから負の二項分布のパラメータを計算してサンプルを生成
    p = mu / var
    n = mu**2 / (var - mu)
    # 主要指標の観測値
    y_obs = nbinom.rvs(n, p, random_state=46)
    scaled_y_obs, y_obs_scaler = MS.max_abs_scaler(y_obs)
    # 施策の観測値
    other_media_obs = np.concatenate([
        np.zeros(200),
        nbinom.rvs(30000, 0.5, size=3, random_state=46),
        nbinom.rvs(15000, 0.5, size=1, random_state=46),
        nbinom.rvs(800, 0.5, size=96, random_state=46)
    ])
    scaled_other_media_obs, media_obs_scaler = MS.max_abs_scaler(other_media_obs)
    # 施策による主要指標観測値への影響係数(真の値)
    alpha = 0.5 # ジオメトリックアドストック関数のパラメータ
    lam = 2.00 # ロジスティックサチュレーション関数のパラメータ
    beta = 0.1 # 主要メディア観測値への影響変数
    apply_geom_adstock = function([], MEM.geometric_adstock(scaled_other_media_obs, alpha))()
    apply_logistic_saturation = function([], MEM.logistic_saturation(apply_geom_adstock, lam))()
    apply_beta_media_coefficient = MEM.media_coefficient(apply_logistic_saturation, beta)
    other_media_effect = media_obs_scaler.inverse_transform(apply_beta_media_coefficient.reshape(-1, 1)).flatten()
    # 観測不可要因による主要指標観測値への影響
    unobservable_media_obs_impact = np.concatenate([
        np.zeros(210),
        np.array([550,600,550]),
        np.zeros(10),
        nbinom.rvs(250, 0.5, size=15, random_state=46),
        np.zeros(5),
        np.array([1500,700, 500, 300, 200, 100]),
        np.zeros(26),
        nbinom.rvs(500, 0.5, size=25, random_state=46)
    ])

実行すると2枚のグラフが保存されます。

こちらは観測不可要因による主要指標への影響があった場合のテストデータです。この場合の推定については後述します。

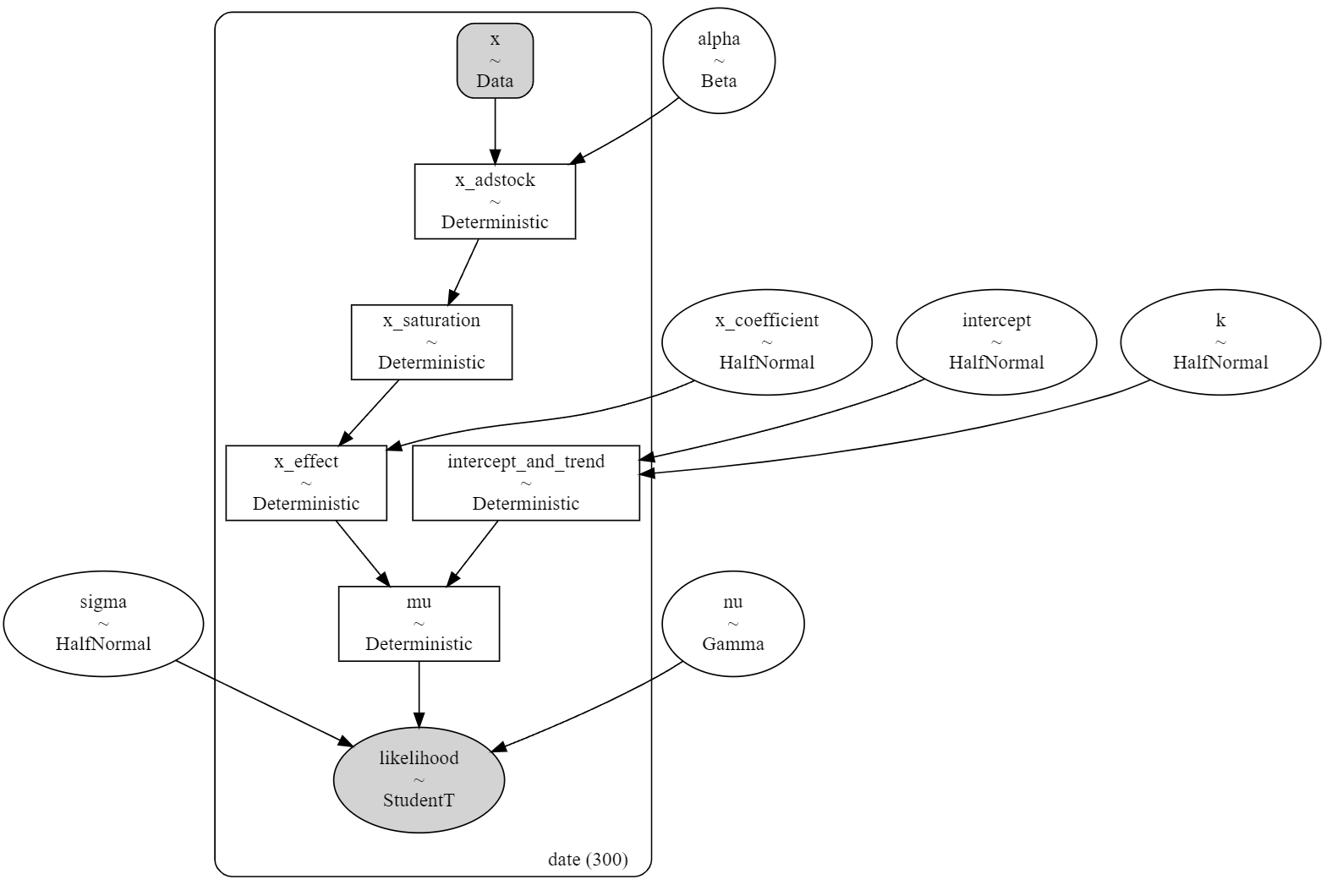
モデル構築

PyMCによるモデルの構築はutil/mcmc_media_effect_estimate.pyで行っています。

mcmc_media_effect_estimate.py

import logging
import os
import sys

sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
import numpy as np
import pymc as pm
from tqdm import tqdm

from util.media_effect_model import MediaEffectModel
from util.metric_scaler import MetricScaler
from util.models import EstimateModelInput, EstimateModelOutput

logger = logging.getLogger(__name__)
logger.setLevel(logging.INFO)
MEM = MediaEffectModel()
MS = MetricScaler()

class MCMCMediaEffectEstimate:
    def estimate(self, input: EstimateModelInput):
        fixed_parameters = input.fixed_parameters
        y = input.y
        x = input.x
        t = input.t
        t_scaled = (t - np.min(t)) / (np.max(t) - np.min(t))
        coords = {"date": t}
        with pm.Model(coords=coords) as model:
            x = pm.MutableData(name="x", value=x, dims="date")
            if 'alpha' in fixed_parameters:
                logger.info("alpha key detected. alpha is not estimated.")
                alpha = fixed_parameters['alpha']
            else:
                alpha = pm.Beta(name="alpha", alpha=1, beta=1)
            if 'lam' in fixed_parameters:
                logger.info("lam key detected. lam is not estimated.")
                lam = fixed_parameters['lam']
            else:
                lam = pm.Gamma(name="lam", alpha=2, beta=1)
            if 'x_coefficient' in fixed_parameters:
                logger.info("x_coefficient key detected. x_coefficient is not estimated.")
                x_coefficient = fixed_parameters['x_coefficient']
            else:
                x_coefficient = pm.HalfNormal(name="x_coefficient", sigma=0.1)
            x_adstock = pm.Deterministic(
                name="x_adstock",
                var=MEM.geometric_adstock(
                    x=x,
                    alpha=alpha
                ), dims="date"
            )
            x_saturation = pm.Deterministic(
                name="x_saturation",
                var=MEM.logistic_saturation(
                    x=x_adstock,
                    lam=lam
                ), dims="date"
            )
            x_effect = pm.Deterministic(
                name="x_effect",
                var=MEM.media_coefficient(
                    x=x_saturation,
                    beta=x_coefficient,
                ), dims="date"
            )

            intercept = pm.HalfNormal(name="intercept", sigma=0.03)
            k = pm.HalfNormal(name="k", sigma=5)
            intercept_and_trend = pm.Deterministic(name="intercept_and_trend", var=intercept + pm.math.exp(-k * (t_scaled - 0.08)), dims="date")
            sigma = pm.HalfNormal(name="sigma", sigma=0.1)
            nu = pm.Gamma(name="nu", alpha=5, beta=2)
            mu = pm.Deterministic(
                name="mu",
                var=intercept_and_trend + x_effect, dims="date"
            )

            # 尤度関数
            pm.StudentT(
                name="likelihood",
                nu=nu,
                mu=mu,
                sigma=sigma,
                observed=y,
                dims="date"
            )

            prior_predictive = pm.sample_prior_predictive()
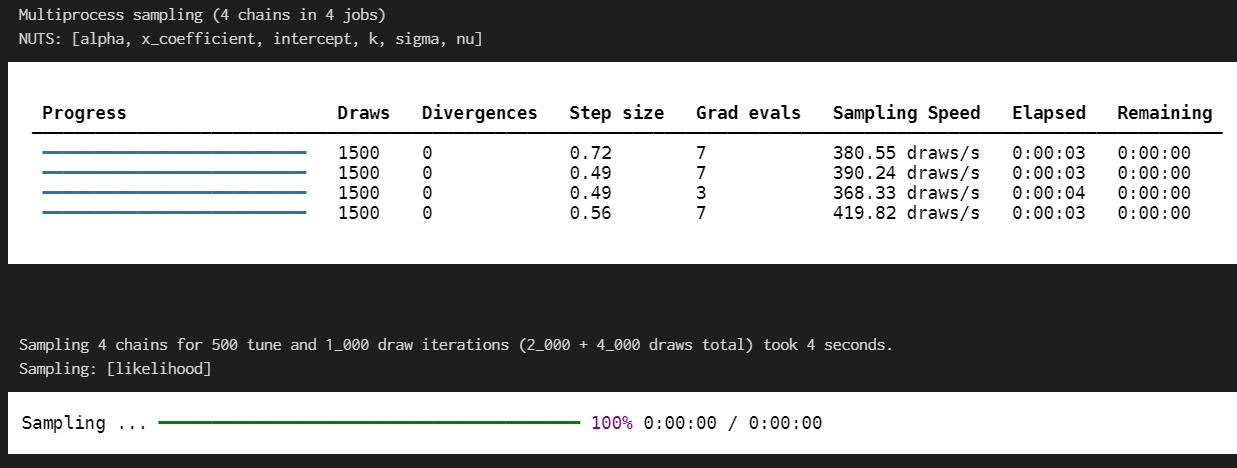
        with model:
            trace = pm.sample(
                tune=500,
                draws=1000,
                chains=4
            )
            model_posterior_predictive = pm.sample_posterior_predictive(
                trace=trace
            )
        return EstimateModelOutput(
            prior_predictive=prior_predictive,
            posterior_predictive=model_posterior_predictive,
            model=model,
            trace=trace
        )

こちらのモデルはMedia Effect Estimation with PyMC: Adstock, Saturation & Diminishing Returnsをとても参考にしています。

主要観測値や施策観測値については、MaxAbsScalerを適用してからモデルに投入します。

estimate.py

import os
import sys
sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
from typing import Dict, List

import pymc as pm
import arviz as az
import numpy as np
from plotly.subplots import make_subplots
import plotly.graph_objects as go
import matplotlib.pyplot as plt
import seaborn as sns

from util.metric_scaler import MetricScaler
from util.mcmc_media_effect_estimate import MCMCMediaEffectEstimate
from util.models import EstimateModelInput, EstimateModelOutput

%load_ext autoreload
%autoreload 2
MS = MetricScaler()
MCME = MCMCMediaEffectEstimate()
def estimate_target_parameters(d: Dict) -> List:
    params = ["alpha", "lam", "x_coefficient", "intercept", "k", "sigma", "nu"]
    return [x for x in params if x not in d]
# 必要なデータをロード
y_obs = np.load("../data/y_obs.npy")
other_media_obs = np.load("../data/other_media_obs.npy")
other_media_effect = np.load("../data/other_media_effect.npy")
unobservable_media_obs_impact = np.load("../data/unobservable_media_obs_impact.npy")
tl = np.load("../data/tl.npy")

y = y_obs + other_media_effect
# y = y_obs + other_media_effect + unobservable_media_obs_impact # 観測不可な要因による主要指標への影響を加えたい場合はこちらを使う
y_scaled, y_scaler = MS.max_abs_scaler(y)
x_scaled, x_scaler = MS.max_abs_scaler(other_media_obs)
fixed_parameters = {"lam": 2} # alpha, lam, x_coefficientについて事前に値を決めたい場合ここに入れる
estimated_target_parameters = estimate_target_parameters(fixed_parameters)
estimate_model_input = EstimateModelInput(
    fixed_parameters=fixed_parameters,
    y=y_scaled,
    x=x_scaled,
    t=tl,
)
estimate_model_output = MCME.estimate(estimate_model_input)

スケーリングされた施策観測値1あたりの効果となる係数は、幾何的アドストック関数、ロジスティックサチュレーション関数を経て、半正規分布の事前分布からサンプリングされます(x_effect)

intercept_and_trendは半正規分布の事前分布から成る切片(intercept)と半正規分布と時系列tに依存した傾き(トレンド)を足して計算されます。

これらを足して$mu$になったのち、自由度$\nu$、分散$\sigma$を設定し、スチューデントのT分布が尤度関数となります。

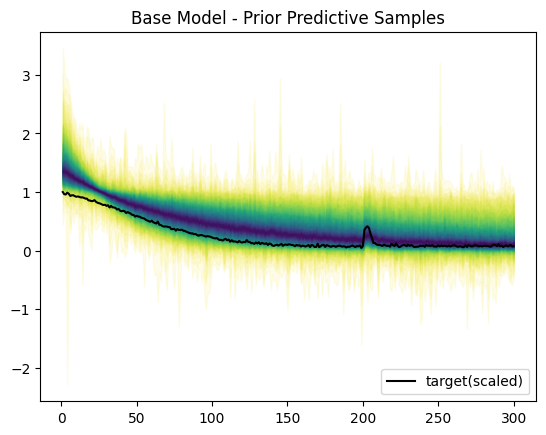
事前分布による生成範囲のプロットです。青いほど確率的に高く、黄色い部分は確率的に低い部分です。
非負の値に対してMaxAbsScalerを使っているので、データ（や現実に推定したい値）は非負の値になります。
今回は尤度関数としてスチューデントのT分布を使っているため、範囲的に負の値も含まれます。

この条件でMCMCによる推定を行います。!

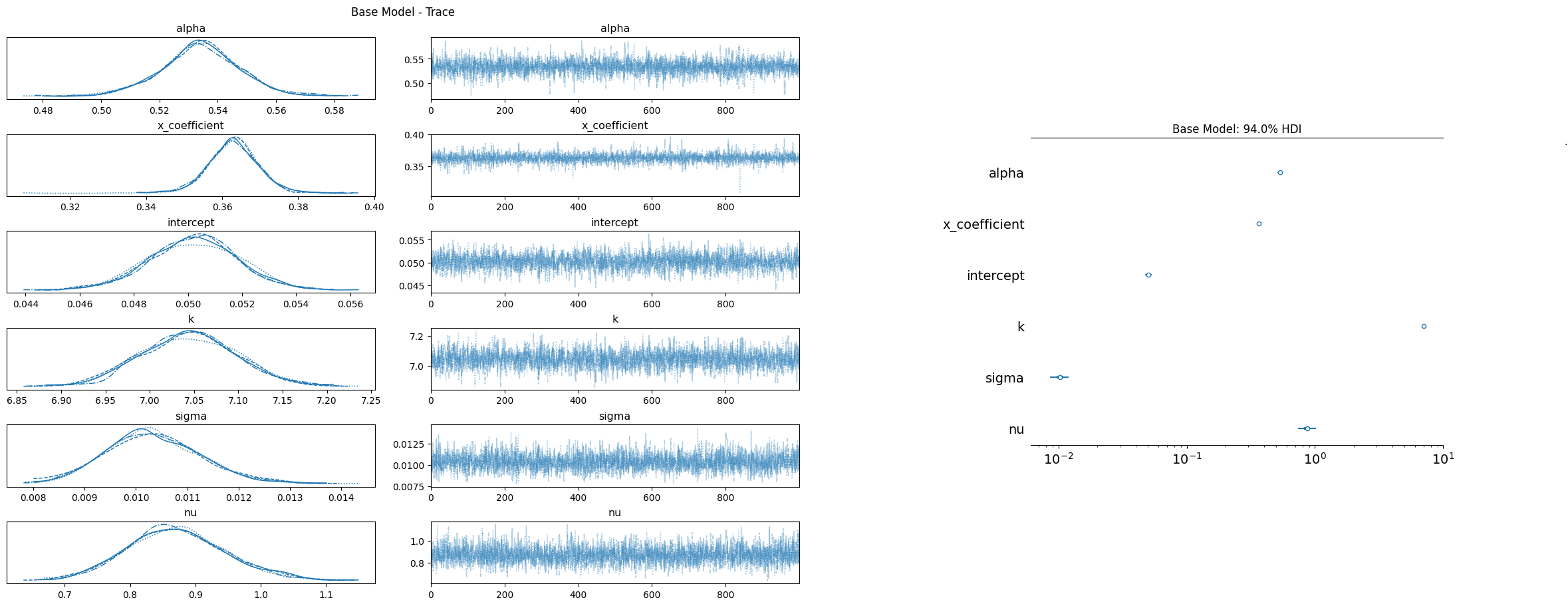
推定結果について、適切に収束しているかを確認しています。
一般的には

• r_hatが1.1未満(下数値表)
• 分布が2峰になっていない（下図一番左）
• 軌跡がランダムウォークのようになっておらずホワイトノイズにようになっている（下図左から2番目）
• 信用区間94%幅が広すぎない（下図一番右）

のようなところを見ます。今回は上記について問題は無いと判断しました。

                mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  
alpha          0.534  0.014   0.508    0.560      0.000    0.000    3254.0   
x_coefficient  0.363  0.007   0.351    0.376      0.000    0.000    3780.0   
intercept      0.050  0.002   0.047    0.053      0.000    0.000    2691.0   
k              7.044  0.055   6.944    7.150      0.001    0.001    2776.0   
sigma          0.010  0.001   0.009    0.012      0.000    0.000    3935.0   
nu             0.871  0.075   0.734    1.021      0.001    0.001    3747.0   

               ess_tail  r_hat  
alpha            2651.0    1.0  
x_coefficient    2418.0    1.0  
intercept        2972.0    1.0  
k                2738.0    1.0  
sigma            2657.0    1.0  
nu               2874.0    1.0  

このまま、主要指標の予測と施策がもたらした主要指標への影響予測について確認します。

estimate.py 一部抜粋

# 主要指標予測結果の確認
posterior_predictive_likelihood = az.extract(
    data=estimate_model_output.posterior_predictive,
    group='posterior_predictive',
    var_names=["likelihood"],
)
posterior_predictive_likelihood_inv = y_scaler.inverse_transform(
    X=posterior_predictive_likelihood
)

posterior_predictive_x_effect = az.extract(
    data=estimate_model_output.trace,
    group='posterior',
    var_names=["x_effect"]
)
posterior_predictive_x_effect_inv = y_scaler.inverse_transform(
    X=posterior_predictive_x_effect
)

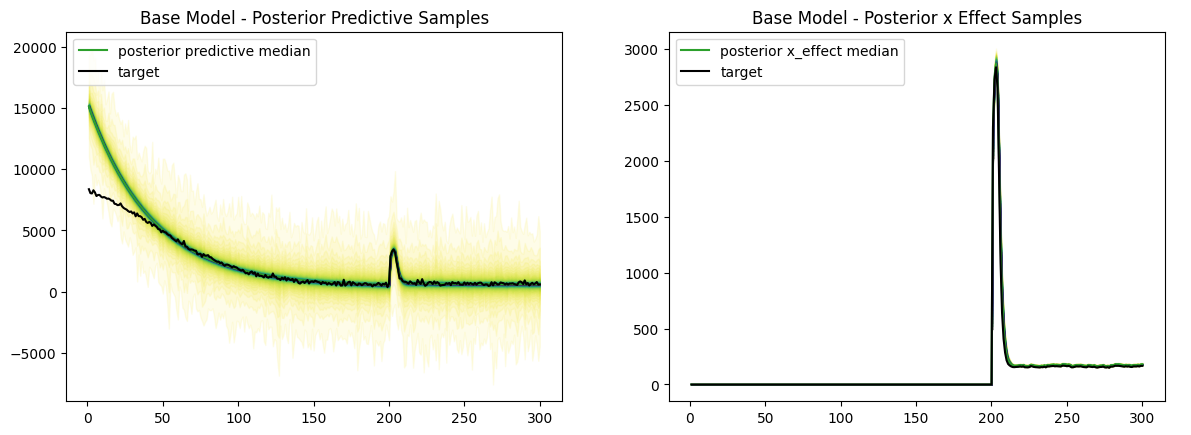
主要指標の予測については、開始点が大きく逸れています。
ですが、施策を行ったのはt=200からであることと、施策がもたらした主要指標への影響については適切に予測できています。

結果

PyMCにより、施策を行った際の主要指標への影響のみを推定することができました。

さらに解釈性を上げる場合は、モデルで用いたx_adstockの推定結果や施策指標1あたり主要指標への影響（係数）についても説明すると良いと思います。

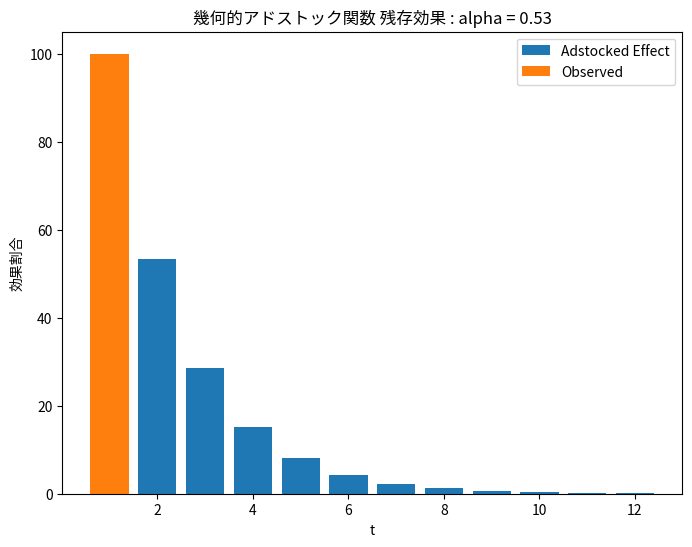
幾何的アドストック関数の推定結果

平均0.534という結果ですが、これは残存効果が53.4%ずつ残っていくという形です。

施策指標1あたり主要指標への影響

これは推定された主要指標への影響 / 施策の観測値を行えばよいだけです。

np.median(posterior_predictive_x_effect_inv, axis=1).sum() / other_media_obs.sum()
0.17328376296447376

観測不可能な主要指標への影響がある場合

デモデータのようにうまく推定できれば良いですが実際は以下のように観測不可な要因による主要指標観測値への影響があると考えられます。

これを含めた状態で推定を行うと想像の通りですが「施策の影響」として影響を取り込んでしまいます。
その結果施策による主要指標への影響が本来より多く導かれてしまいます。

r_hat値も高く、alpha（残存効果）のmeanも高く出ています。

                mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  \
alpha          0.708  0.073   0.522    0.765      0.025    0.025      18.0   
x_coefficient  0.353  0.012   0.331    0.374      0.001    0.000     122.0   
intercept      0.046  0.004   0.040    0.056      0.001    0.001      20.0   
k              6.961  0.112   6.772    7.194      0.028    0.019      21.0   
sigma          0.014  0.001   0.012    0.017      0.000    0.000    2912.0   
nu             0.858  0.079   0.715    1.013      0.001    0.001    2918.0   

               ess_tail  r_hat  
alpha              28.0   1.17  
x_coefficient    1877.0   1.03  
intercept          33.0   1.16  
k                  31.0   1.15  
sigma            2520.0   1.00  
nu               2434.0   1.00  

これを解決するには、主要指標において要因が入っていないデータからパラメータを推定し、その値を固定して使うが現状いい方法かなと思っています。

つまり今回の推定で行った「影響を推定するために理想的なデータ」を担当者などと協力して探し、それにより導かれたパラメータを代表的な値として使うことです。（事前分布に反映する・固定値にする）

ベイズモデリングはそのような経験による値を反映できるので、十分に調査し問題なさそうであればある程度的を得た推定はできるのかなと思っています。

さいごに

ここまで読んでいただきありがとうございました。
もし他にいい案やご指摘等あればコメントで教えていただけると嬉しいです。

参考