PHPでニューラルネット: 関数近似編

こんにちは皆さん

機械学習というと今までよくわからん、ふわっとした雲の上の世界の話でしたが、自分で実際にニューラルネットを実装してみると、どういうところで苦労するのかとかがある程度見えてきます。

前回はニューラルネットをそのままプログラムに落としてみましたが、今回は実際の例を見ることによって、機械学習がどのように行われるのかというのを見てゆくことにしましょう。

事前準備

使用関数

層状ニューラルネットを考えた時、各層にそれぞれ適当な関数を設置するわけですが、今回使う関数のコードを書いておきます。

Relu.php

<?php

namespace Niisan\phpnn\layer;

class Relu extends Base
{

    public function activate($val)
    {
        if ($val > 0) {
            return $val;
        }

        return 0;
    }

    public function defferential($val)
    {
        if ($val > 0) {
            return 1;
        }

        return 0;
    }
}

これはreluと呼ばれる関数で、入力値が0より大きければその入力値を返し、0以下であれば0を返します。微分は0以下であれば0, そうでなければ1となります。

Linear.php

<?php

namespace Niisan\phpnn\layer;

class Linear extends Base
{

    public function activate($val)
    {
        return $val;
    }

    public function defferential($val)
    {
        return 1;
    }
}

これは単純な線形関数$y=x$です。

HyperbolicTangent.php

<?php

namespace Niisan\phpnn\layer;

class HyperbolicTangent extends Base
{

    protected $max = 1;
    protected $offset = 0;

    public function activate($val)
    {
        return $this->max * (tanh($val) + $this->offset) ;
    }

    public function defferential($val)
    {
        $temp = tanh($val);
        return $this->max *(1 - $temp * $temp);
    }
}

これは双曲線関数の中でハイパボリックtanと呼ばれるものです。
出力の値が$[-1,1]$の範囲に収まるため、２値信号や非線形の関数出力としてよく使われます。

今回はこれらの関数をニューラルネットに使用していきます。

誤差関数

誤差関数は次の関数を使用します。$y = F(x)$に対し、真の値$z$とすると、

L(y, z) = \frac{1}{2} || z-y ||^2 = \frac{1}{2} \sum_i (z_i - y_i)^2

\frac{\partial L}{\partial y} = (y_1 - z_1, y_2-z_2, ... , y_n - z_n)

逆誤差伝播の入力値として、この微分値を使います。

sin(x)cos(x)

手始めに$y=\sin x \cos x$をニューラルネットで近似してみましょう。

実装

以下のコードを使って近似を実施してみます。

sinApproximate.php

<?php

require('../vendor/autoload.php');

use Niisan\phpnn\layer\Relu;
use Niisan\phpnn\layer\HyperbolicTangent;
use Niisan\phpnn\layer\Linear;

$bundle = new Niisan\phpnn\bundle\Simple();

$effect = 0.1;
$bundle->add(Relu::createInstance()->init(1, 64, ['effect' => $effect]));
$bundle->add(HyperbolicTangent::createInstance()->init(64, 64, ['effect' => $effect]));
$bundle->add(Relu::createInstance()->init(64, 64, ['effect' => $effect]));
$bundle->add(Linear::createInstance()->init(64, 1, ['effect' => $effect]));

$check = [];
$title = [];
for ($i = 1; $i < 12001; $i++) {
    $x = mt_rand(-10000, 10000) * pi() / 20000;
    $y = $bundle->exec($x);
    $bundle->correct(sin($x)*cos($x));
}

結果

結果をプロットしてみましょう。
ループを何回回した時点で、どの程度近似が進んでいるでしょうか

関数の極小値付近で、ループ回数の少ない緑の線は、実際の値に比べて随分と離れています。
それに比べ、ループ数の多い赤、青では極大・極小近傍では割と良い近似になっていることがわかります。
ただ、赤と青でそれほど大きな違いがなく、近似が停滞しているように見えます。
つまり、大量に回数を重ねても精度が上がるかどうかは保証できません。

ドーナッツ型の信号

二つの入力がある条件を満たした時だけ1を出力するような関数$f(x, y)$を考えましょう。

f(x, y) = \left\{
\begin{array}{1}
1, (1 < x^2 + y^2 < 4)\\
-1,  ( \rm{otherwise} )
\end{array}
\right.

この関数を平面上に図示すると、ドーナッツ上の図形が現れます。
果たしてニューラルネットはこれを出力できるでしょうか？

実装

今回は中間層にハイパボリックtanを一つ、出力層にもう一つ使います。

targetHit.php

$bundle = new Niisan\phpnn\bundle\Simple();

$effect = 0.005;
$bundle->add(Relu::createInstance()->init(2, 32, ['effect' => $effect]));
$bundle->add(HyperbolicTangent::createInstance()->init(32, 64, ['effect' => $effect]));
$bundle->add(Relu::createInstance()->init(64, 32, ['effect' => $effect]));
$bundle->add(HyperbolicTangent::createInstance()->init(32, 1, ['effect' => $effect]));

for ($i = 1; $i < 100001; $i++) {
    $x = mt_rand(-20000, 20000) / 10000.0;
    $y = mt_rand(-20000, 20000) / 10000.0;
    $z = $bundle->exec([$x, $y]);
    $ishit = donuts($x, $y);
    $bundle->correct($ishit);
}

function donuts($x, $y)
{
    $r = $x * $x + $y * $y;
    if ($r > 1 and $r < 4) {
        return 1;
    }

    return -1;
}

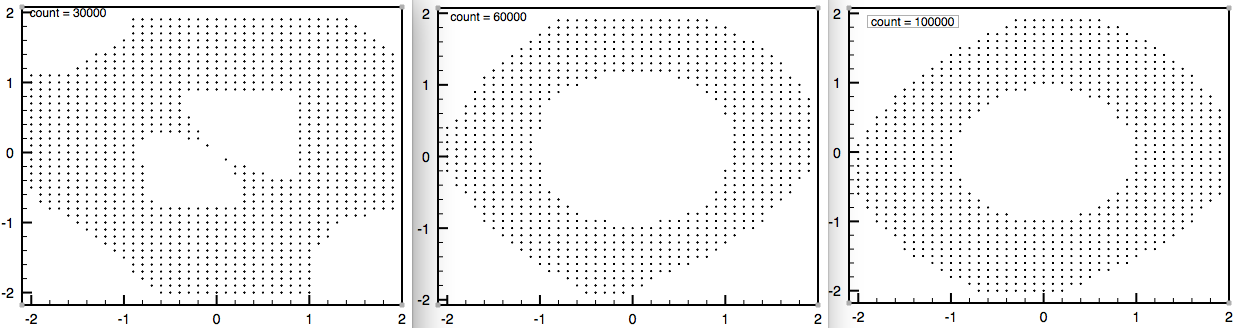
さて、結果はどうでしょうか

結果

一番左はループ回数が30000回のものです。形は歪で、中央部分がちょっと変な形を指定ます。
しかし、60000回繰り返すと形状はドーナッツ上のものに近づきます。
同様に100000回繰り返しても、60000回のものとは形状こそ違え、ドーナツ状のものが現れます。

この結果を見るに、60000回を超えると、精度があまり変わっていないように思えます。

大変なこと

さて、今回の実験ですが、実はそんな簡単にできませんでした。ニューラルネットで近似するとか機械学習でとにかく大変なのは、これから見ていく細かい調整にあります。

層とノードの数をどうするのか

ノードとは、各層が持っている要素の数なのですが、層とノードの個数をどうするのかが一つの関門となります。
層とノードが多ければ多いほど、良い近似になるだろうとは思うのですが、層の数やノードの数が増えると、必要な計算量が飛躍的に増えてしまいます。
つまり、計算時間と相談して、かつ、いい感じになりそうな層の数とノードの数を見定める必要があるというわけです。

関数をどうするのか

各層が入力値から何らかの出力を出すわけですが、この出力値を出すための関数をどうするかがやはり重要になります。
例えば、ふたつ目の関数近似では中間層の一つにハイパボリックtanを使用しています。
これははじめからそうなっていたわけではなく、線形関数を使っているとどうしてもドーナッツ型に近づかなかったため、使わざるを得なかったという感じです。
結局、どのような関数を選ぶかは、誤差がちゃんと収束するかどうかを観察して、決めていくしか無いのです。

学習率の調整

各層の重み$w_{ij}$を誤差から導かれる微分値を使って、修正しますが、その時の修正度合いである学習率も重要な調整要素になります。
学習率が大きすぎれば、各$w_{ij}$の値が乱高下してしまい、収束しなかったり発散してしまったりします。
一方で学習率が小さすぎると、やはり収束に向けた速度が遅くなります。
つまり、現実的な時間で近似の収束を終わらせるのに最適な学習率を決めてやらなければならないということです。
これを決めるには何度か試してみていい感じに収束しそうな値を選ぶしかありません。

まとめ

せっかくニューラルネットを自作したのだからと、関数近似をやってみましたが、思ったより大変でした。
次回は強化学習に使ってみようと思います。