こんにちはみなさん
Googleさんがmagentaという自動作曲学習器を作ってくれたので、これで私の好きな感じの曲がいくらでも作れるぞ！と思ったのですが、実際にはそう簡単には行きませんでした。
学習元のファイルはmidiらしく、録音したファイルを何でもかんでもぶち込んで、学習できるわけではない模様。
というわけで、wavを使って作れる自動作曲学習機って自作できないもんかねって動機で、色々試してみました。
ここ数回の記事は今回のための実験ですね。
TL;DR
- midiよくわからないんで、wavで自動作曲したいな
- KerasにstatefulなRNNというのがあるらしいので使ってみよう
- 256フレームのフーリエ変換を入力にした学習器・ジェネレータを作ってみた
- 学習はできるが、今のところうまく行っていない
- python (numpy) の勉強にはなった！
リポジトリは以下のものを使ってます
https://github.com/niisan-tokyo/music_generator
実際の学習は以下のファイルを使います。
https://github.com/niisan-tokyo/music_generator/blob/master/src/stateful_learn.py
動機
Googleさんがtensorflowを使用した自動作曲ツール、magentaをリリースしました。
https://magenta.tensorflow.org/
これは素晴らしいツールなんですが、対象ファイルがmidiなので、ちょっと自分には馴染みがないのです。
(昔はたくさんあったんですが、最近はmp3が多いし。。。)
とりあえず録音したファイルを手軽に扱うには、wavのような波形そのもののデータを使うのが良さそうで、
しかもpythonにはwavをネイティブに取り扱うことができるというので、これはもうやってみるっきゃないって思いました。
計画
生の波形データをそのまま学習に使用するのも考えましたが、まるで使い物にならなかったので、次のようなプランを考えました。
- 波形データを一定区間ごとにフーリエ変換し、周波数の複素振幅の時間変遷を取得する
- statefulなRNNに複素振幅の時間変化を学習させる
- 学習完了したものにサンプルとして少量の音を入力すると、逐次音を作り出す。。。はず
つまり、こんなのが作れるんじゃないかなって思いました
時系列の周波数分布が得られれば、これをフーリエ逆変換することで音楽ができるって寸法です。
フーリエ変換
前回の記事において、256フレームのフーリエ変換に対し、逆変換で戻したwavファイルが、問題なく聞けるものだったので、
音自体を表す特徴量としてはこれで十分じゃないかって思います。
http://qiita.com/niisan-tokyo/items/764acfeec77d8092eb73
numpyのライブラリで高速フーリエ変換(FFT)をすると、例えば256フレームの区間であれば、256個の周波数分布が得られます。
普通、音声ファイルのフレームレート(一秒あたりのフレーム数)は44100ですので、256 / 44100 = 5.8 (msec) ごとの周波数分布が得られることになります。
この5.8msecごとの時間変遷を自動生成できる学習機を作れれば、音楽が自動的にできていくんじゃないかなっていう考え方
stateful RNN
RNNと言うのは再帰ニューラルネットワーク(Recurrent Neural Network)のことで、入力から出力を得る際に、以前に計算した内容を参照することで、連続した状態を取り扱うネットワークの種類です。
http://qiita.com/kiminaka/items/87afd4a433dc655d8cfd
KerasでRNNを取り扱う場合、通常は連続した幾つかの状態を入力とし、出力を作りますが、各入力において、前回の状態はリセットされてしまいます。
stateful RNNではこの前回の処理後の状態を保ったまま、次の処理を行います。
これによって、不定期間の複雑な系列処理ができるのではないかと期待されます。
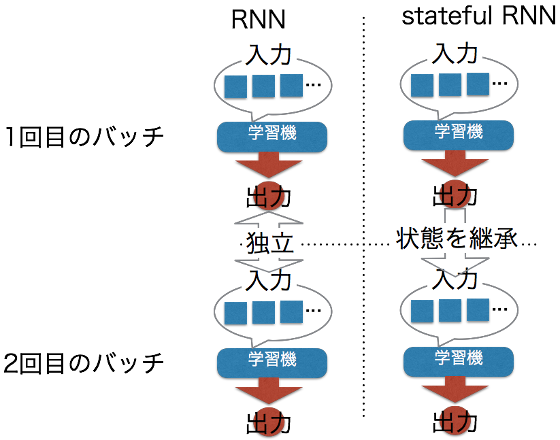
今回は入力を現在の瞬間の周波数分布、出力を次の瞬間の周波数分布として逐次的にstateful RNNで学習させ、曲の流れというものを持ったジェネレータが作れるんじゃないかって考えました。
学習準備
ファイルの準備
m4aやmp3ファイルなら、ffmpegを使ってwavに変換できます。
http://qiita.com/niisan-tokyo/items/135824905e4a3021d358
好きなゲーム音楽をmacで録音して、wavに吐き出してます。
データセットの作成
データセットはwavをフーリエ変換して作るので、基本的にはコードを参照すれば良いですが、一部注意点があります。
def create_test_data(left, right):
arr = []
for i in range(0, len(right)-1):
#複素数のベクトル化
temp = np.array([])
temp = np.append(temp, left[i].real)
temp = np.append(temp, left[i].imag)
temp = np.append(temp, right[i].real)
temp = np.append(temp, right[i].imag)
arr.append(temp)
return np.array(arr)
これはフーリエ変換したステレオ音源の周波数分布を結合させて入力用のデータを作っている部分です。
ここでは複素数で表される周波数分布の実部と虚部をベクトルの別々の要素に入れ直しています。
これは、複素数のまま計算しようとすると、虚部が落とされてしまうためです。
これらにより、一区間のサンプリング数は256フレームですが、実際の入力次元は1024になります。
学習する
モデルの作成
モデルは単純にLSTMを３つ連結させて、最後に全結合層入れるだけの簡単なものです。
model = Sequential()
model.add(LSTM(256,
input_shape=(1, dims),
batch_size=samples,
return_sequences=True,
activation='tanh',
stateful=True))
model.add(Dropout(0.5))
model.add(LSTM(256, stateful=True, return_sequences=True, activation='tanh'))
model.add(Dropout(0.3))
model.add(LSTM(256, stateful=True, return_sequences=False, activation='tanh'))
model.add(Dropout(0.2))
model.add(Dense(dims))
model.compile(loss='mse', optimizer='adam')
さて、statefulなRNNを使用する際には幾つか条件があります。
まず、一つのバッチあたりの入力次元を指定しなければなりません。
次に、前のバッチの各サンプルと次のバッチの各サンプルが系列として連続でなければなりません。
具体例としては、一つ目のバッチX_1と２つめのバッチX_2があったとすると、両者のi番目のサンプル$X_1[i]$, $X_2[i]$の間には関連がないといけないということです。
今回はジェネレータが$x_{n+1} = RNN(x_n)$でできていると考えて、複数の連続した状態から次の同数の状態のセットを作る、と言うかたちを想定しています。
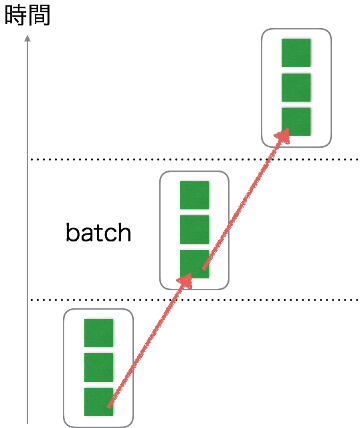
つまり、$X_2[i]$は$X_1[i]$に対して、常にサンプル数の分だけ先の状態になっているということになります。
ちょっといい加減すぎる気もしないでもないですが、こんな感じでサンプルの数、つまり32こずつ次の状態を作るというのを繰り返す機械とみなします。
フィッティング
準備ができたので学習を開始しましょう。
for num in range(0, epochs):
print(num + 1, '/', epochs, ' start')
for one_data in test:
in_data = one_data[:-samples]
out_data = np.reshape(one_data[samples:], (batch_num, dims))
model.fit(in_data, out_data, epochs=1, shuffle=False, batch_size=samples)
model.reset_states()
print(num+1, '/', epochs, ' epoch is done!')
model.save('/data/model/mcreator')
学習時にはバッチの順番が重要になりますので、バッチ上のサンプルをshuffleさせないようにしています。
また、各wavごとに学習を行い、一回学習後は内部状態をリセットさせています。
結果
学習結果
まず、学習させてみると、なんとなくフィッティングが進んでいるように見えます。
1 / 10 start
Epoch 1/1
16384/16384 [==============================] - 87s - loss: 1.9879e-04
Epoch 1/1
16384/16384 [==============================] - 84s - loss: 1.9823e-04
Epoch 1/1
16384/16384 [==============================] - 75s - loss: 1.1921e-04
Epoch 1/1
16384/16384 [==============================] - 82s - loss: 2.3389e-04
Epoch 1/1
16384/16384 [==============================] - 80s - loss: 3.7428e-04
Epoch 1/1
16384/16384 [==============================] - 90s - loss: 3.3968e-04
Epoch 1/1
16384/16384 [==============================] - 87s - loss: 5.0188e-04
Epoch 1/1
16384/16384 [==============================] - 76s - loss: 4.9725e-04
Epoch 1/1
16384/16384 [==============================] - 74s - loss: 3.7447e-04
Epoch 1/1
16384/16384 [==============================] - 87s - loss: 4.1855e-04
1 / 10 epoch is done!
2 / 10 start
Epoch 1/1
16384/16384 [==============================] - 82s - loss: 1.9742e-04
Epoch 1/1
16384/16384 [==============================] - 85s - loss: 1.9718e-04
Epoch 1/1
16384/16384 [==============================] - 90s - loss: 1.1876e-04
Epoch 1/1
16384/16384 [==============================] - 104s - loss: 2.3144e-04
Epoch 1/1
16384/16384 [==============================] - 97s - loss: 3.7368e-04
Epoch 1/1
16384/16384 [==============================] - 78s - loss: 3.3906e-04
Epoch 1/1
16384/16384 [==============================] - 87s - loss: 5.0128e-04
Epoch 1/1
16384/16384 [==============================] - 79s - loss: 4.9627e-04
Epoch 1/1
16384/16384 [==============================] - 82s - loss: 3.7420e-04
Epoch 1/1
16384/16384 [==============================] - 90s - loss: 4.1857e-04
2 / 10 epoch is done!
...
これで出来上がったモデルを使って音を作ってみます。
音の生成
詳細なコードはリポジトリのstateful_use.pyに譲りますので、大まかな流れのみを書くと、
- 生成されたモデルを読み込み
- 種となる音楽ファイルを読み込み
- 種を使ってある程度モデルにpredictさせて時系列データを作成し、
- 自分自身が生成した時系列データから次の状態を逐次作成する
- ある程度の長さ時系列データが生成できたら、それを元に逆フーリエ変換から元の波形データを作る
ジェネレータ部分は以下のとおりです
# 種ファイルのフーリエ変換
Kl = fourier(left, N, samples * steps)
Kr = fourier(right, N, samples * steps)
sample = create_test_data(Kl, Kr)
sample = np.reshape(sample, (samples * steps, 4 * N))
music = []
# 種データをモデルに入力 => 状態を「醸成」する
for i in range(steps):
in_data = np.reshape(sample[i * samples:(i + 1) * samples], (samples, 1, 4 * N))
model.predict(np.reshape(in_data, (samples, 1, 4 * N)))
# 種データで状態を変更済みのモデルに、最後に出力したデータを逐次代入し、音楽を自己生成
for i in range(0, frames):
if i % 50 == 0:
print('progress: ', i, '/', frames)
music_data = model.predict(np.reshape(in_data, (samples, 1, 4 * N)))
music.append(np.reshape(music_data, (samples, 4 * N)))
in_data = music_data
music = np.array(music)
こうして得られたデータを逆フーリエ変換し、実空間にした後、wavに書き込むわけです。
実空間での波形を見てみると、以下のようになりました。
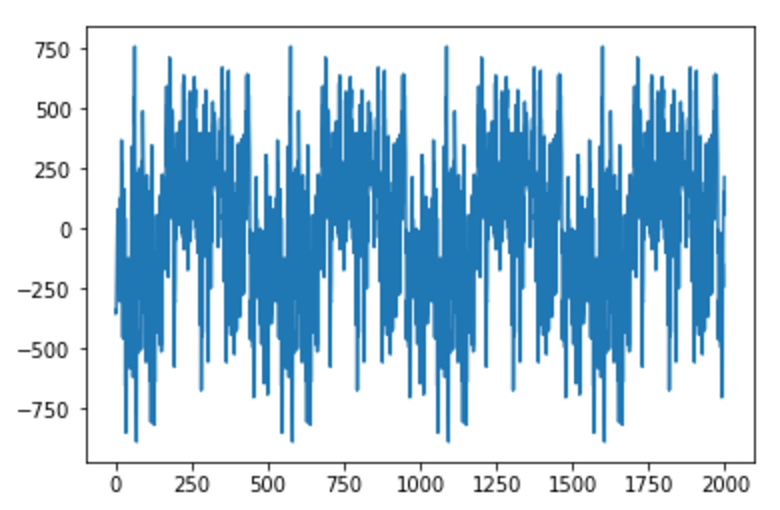もう少し長いスパンのもの
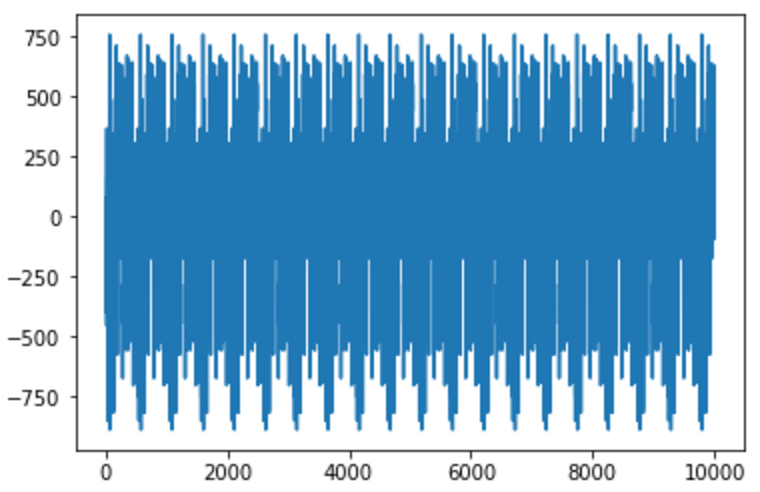こいつをwavで聞くと、「ブー」という一定音階のブザー音がずーっと流れるというシュールな状態になっています。。。
音楽どころか、定常的な音を出すだけの謎機械になってしまいました。
どんな音楽ファイルを入れても同じような音をだすようになってました。
考察
うまくいかなかった理由としては、音の変遷が激しいため、結局最も誤差が少なくなるような定数をとる方向に学習が進んでしまったのではないかと思います。
複雑な系にもかかわらず、誤差の変動が少なすぎるのもそのためかと。
ステートレスでやろうとすると、シーケンス数をどれだけ取ればよいのかわからず、シーケンスの分だけ次元が増えていき、気軽に学習できなくなったりするのが悩みどころです。
もしくは学習回数が少なすぎるというのもあるかもしれませんが、すでにlossがえらく小さいので、考えどころが違うのかもしれないです。
どちらにしろ、もっと改善する必要があります。
まとめ
そんなに簡単に曲ができたら、それほど楽なことはないですよね。
あまりうまくはいかなかったものの、pythonの使い方、特にnumpyの意味とかがある程度わかってきたように思うので、その点は良かったかと思います。
あと、どうでもいいですが、numpyのreshapeめっちゃ勉強する羽目になりました。
今回はこんなところです
追記
2017/06/18
以下の変更を加えました。
- フーリエ変換のサンプル数N: 256 -> 1024
- フーリエ変換時の定数: (n/2) -> 100
- LSTMユニット数: 256 -> 512
- バッチ数: 512 -> 128
結果
以下のような波形を得ました。
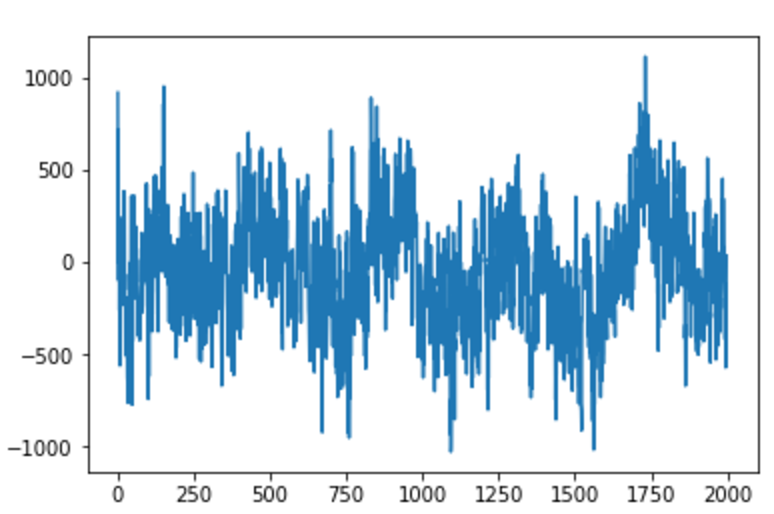
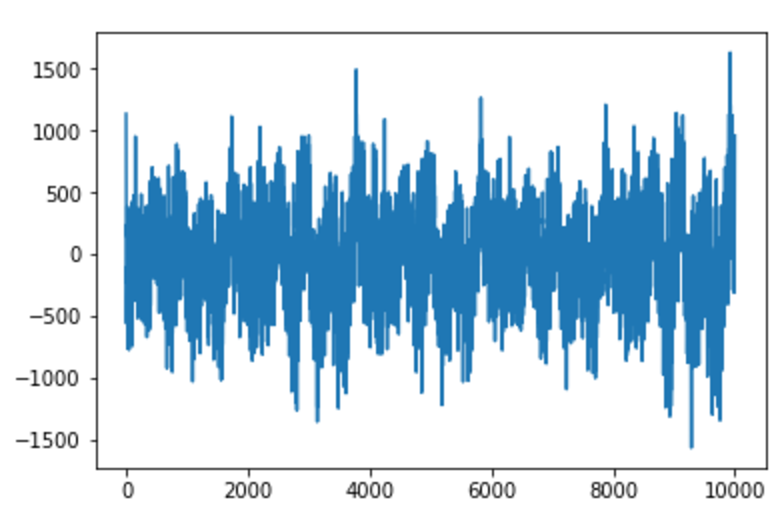
相変わらず背景ノイズは残っていましたが、一定のリズムを刻んでいるように聞こえるようになりました。
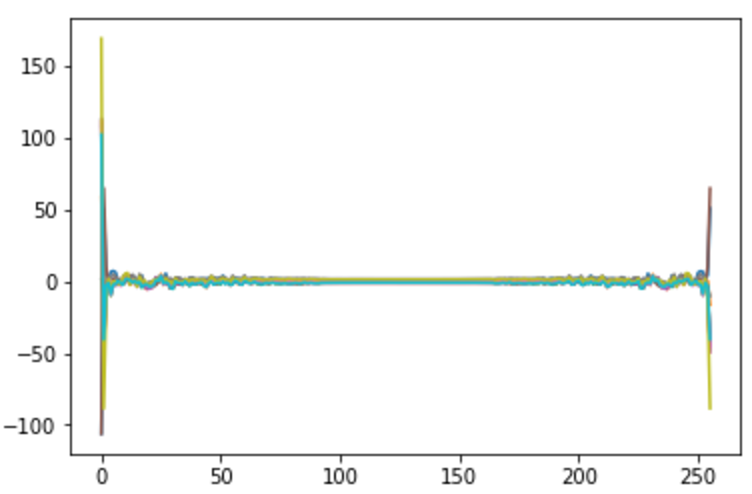
また、得られる周波数分布(の実部)は以下のようになりました。
５フレームずつ,10個分の分布図を重ねています。
N=256, LSTMニューロン数=256
N=1024, LSTMニューロン数=512
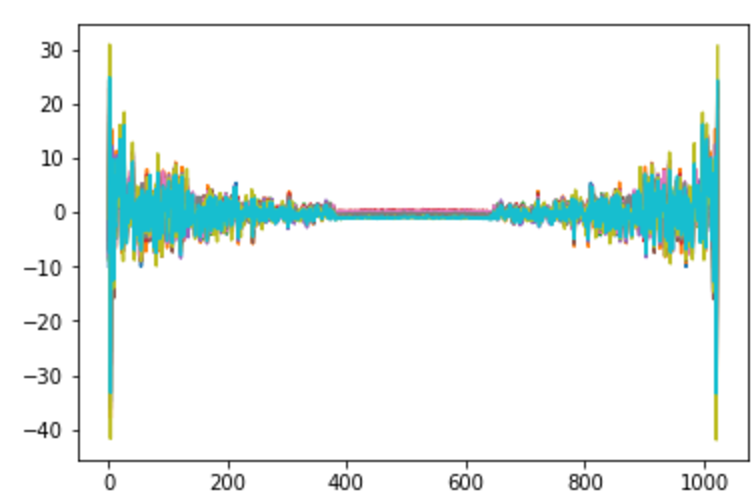
なお、N=1024, ニューロン数256だと、N=256の場合と同じようになった。
考察
フーリエ変換した際に、かけるファクターを変えたところ、当然ですがlossが増大しました。lossにはmseを使用しているので、ファクターを変えると、lossは2乗で増加します。
これにより、より小さい成分の変化を観測できるようになり、逆に精度が上がった可能性があります。
また、ニューロン数を増加させることで、表現力が上昇しました。
改善としてはフーリエ変換時にかけるファクターを増やしたり、ニューロン数を更に増加させることが考えられます。
epoch数が10, 元曲数が9なので、これを変更してもよいのですが、lossの変化が乏しいので、イマイチ効果が見えなかったので、とりあえず保留かと。