はじめに
私が統計を勉強してきた中で特に重要だと思った「相関関係と因果関係」について解説していこうと思います!
この「相関関係と因果関係」の違いがわかると、なぜデータを可視化するだけでは因果関係を説明できないのかといった統計分析を行う意義がわかると思います!
特に、統計を全く知らないよという方でも理解していただけるように噛み砕いて説明しているのでご安心ください。
それでは一度、相関関係と因果関係の定義をおさらいしましょう。
最初にしっかりとした定義を説明した後でわかりやすく噛み砕いて説明します!
相関関係とは
相関関係とは、ある要素とある要素が互いに関係しあっていることを表します。
いわば、ご近所さんのような関係になっています。なぜなら、相関係数のみではそれぞれの要素はどちらかに対しての原因や結果なのかどうかは変わらないため、たまたま隣になったご近所さんだ!って思ってもらうのが一番いいです。
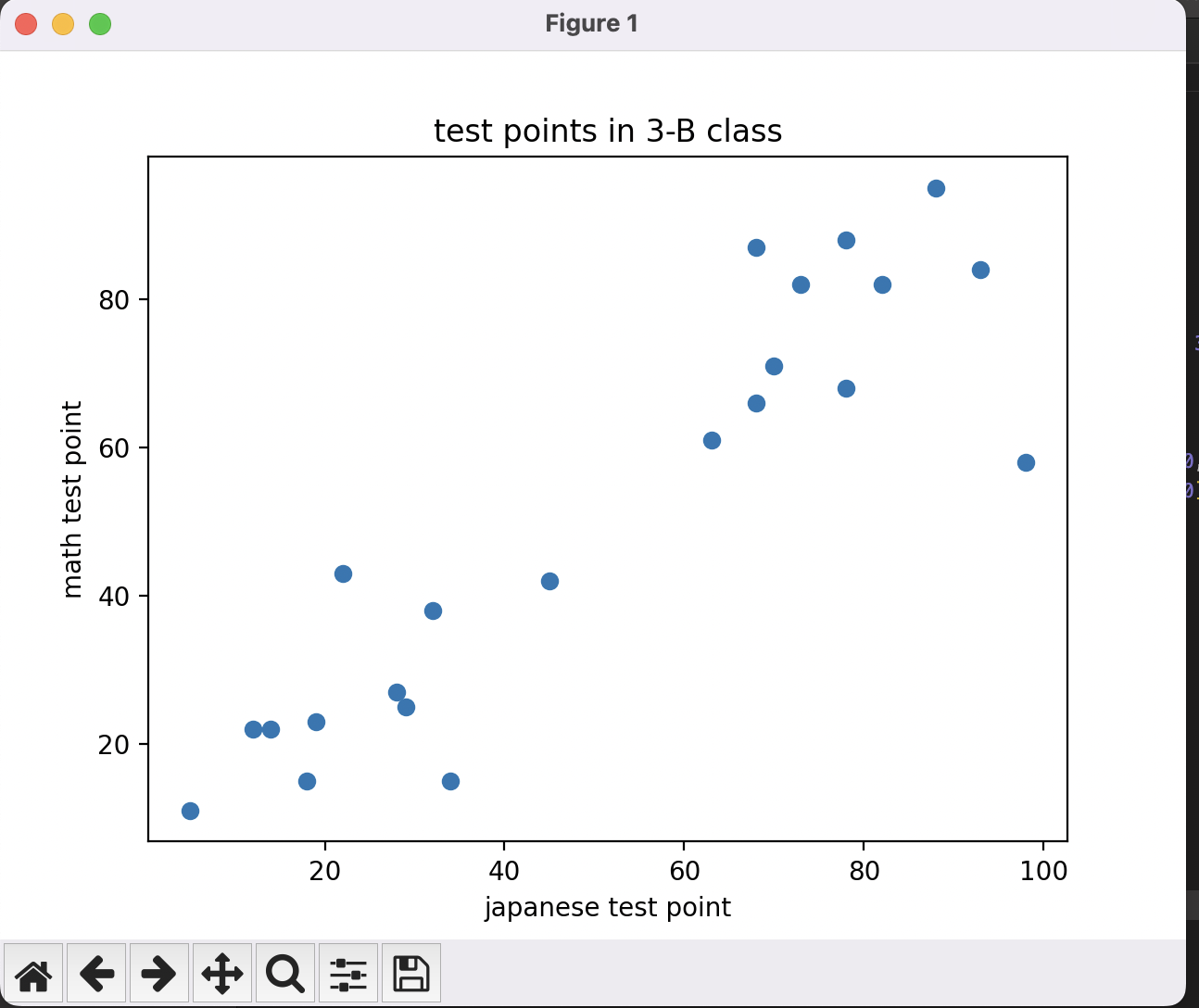
例えば、3年B組のクラス30人の数学と国語の点数を以下のようになグラフで見ると、「数学の点数が高いほど、国語の点数が高い」また、「数学の点数が低いほど、国語の点数が低い」ことが言えます。また、相関係数は0~1までの数字を取り、数字が大きいほど相関が強い、つまりお互いの要素が互いに関係しあっているということが言えます。ちなみに今回の相関係数は0.90491となっていました。これはめちゃんこ強い相関となっています!
実装コードはこちらです。
import matplotlib.pyplot as plt
import matlab as ml
import pandas as pd
# 3年B組30人分の国語のテスト
japanese = [5.0, 73.0, 29.0, 63.0, 68.0, 28.0, 45.0, 78.0, 70.0, 93.0,
82.0, 88.0, 98.0, 68.0, 78.0, 12.0, 32.0, 18.0, 19.0, 22.0, 34.0, 14.0]
# 3年B組30人分の数学のテスト
math = [11.0, 82.0, 25.0, 61.0, 66.0, 27.0, 42.0, 88.0, 71.0, 84.0, 82.0,
95.0, 58.0, 87.0, 68.0, 22.0, 38.0, 15.0, 23.0, 43.0, 15.0, 22.0]
# 相関係数を求める
corrcoef = ml.corrcoef(japanese, math)[0, 1]
print(corrcoef)
# 散布図を描く
plt.scatter(japanese, math)
plt.title("test points in 3-B class")
plt.xlabel("japanese test point")
plt.ylabel("math test point")
plt.show()
因果関係とは
因果関係とは、原因と結果の関係にあることをいいます。
ある要素が原因となって結果が生じるという、相関関係では明確でなかった部分を明確にした関係であると言えます。
また、因果関係では、時間順序(出来事の起こる順番がある)と直接性(お互いが直接的に関係していること)という特徴があります。
いろんな具体例があると思いますが、ここではイメージを掴んでもらおうと思います。
因果関係には、相関関係にはなかった「アクション」というものが存在します。
アクションは原因に該当し、何か結果につながるアクションがあったからこの結果が生じたということです。
今回は、因果関係を見る一つの手法として回帰分析という使用します。(今回は単回帰分析)
回帰分析とは説明変数X(原因)を1単位増減させたときに、被説明変数Y(結果)がどの程度変動するかを出力する分析手法です。
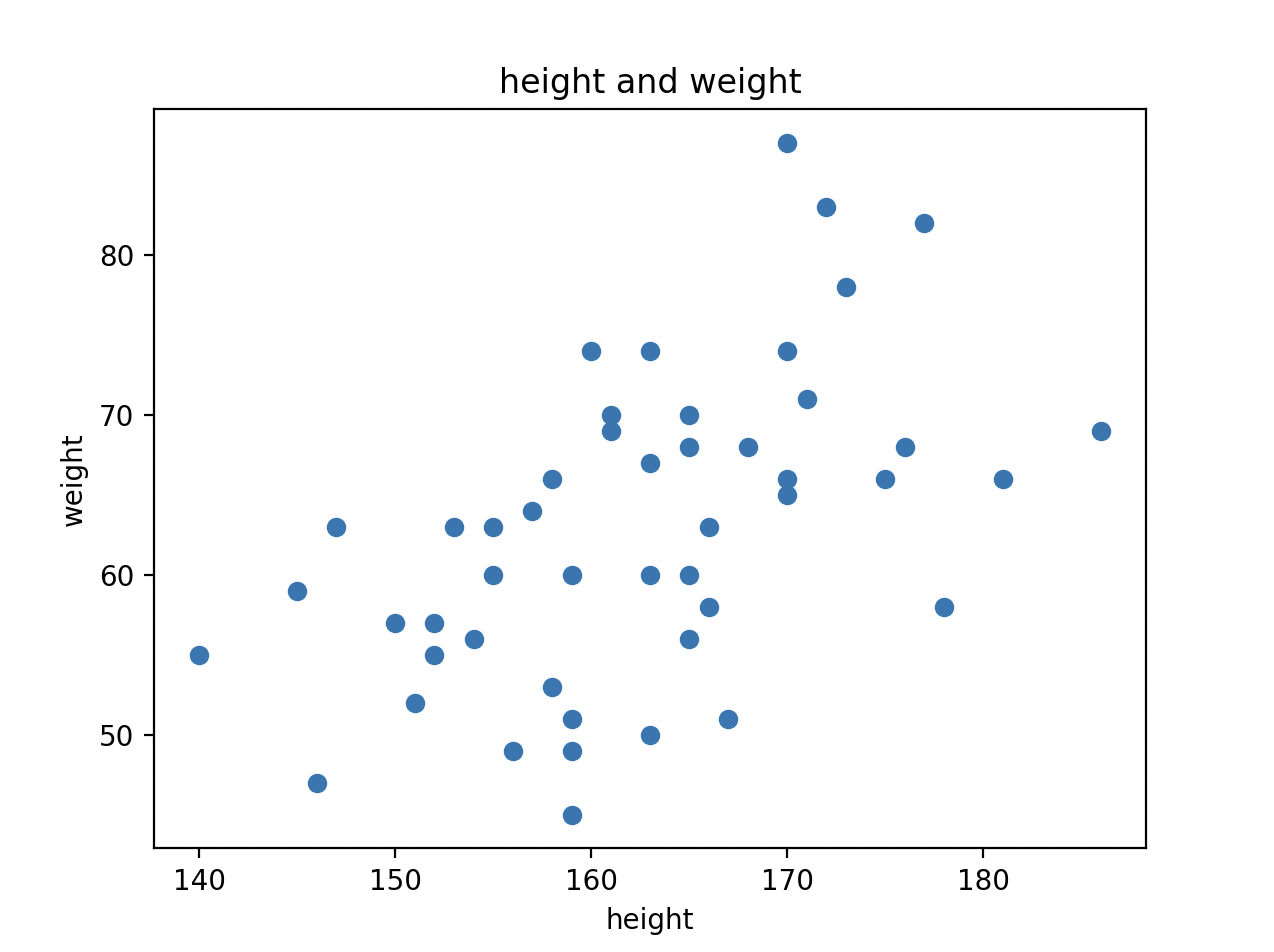
例えば3年B組の生徒の身長と体重について分析を行う際、単なる相関も出すことができますが、実際に回帰分析を行うことで今回の場合は身長が体重にどのように影響があるのか因果関係を見ることができます。(実際に因果関係があるかどうかは分析してからのお楽しみ)
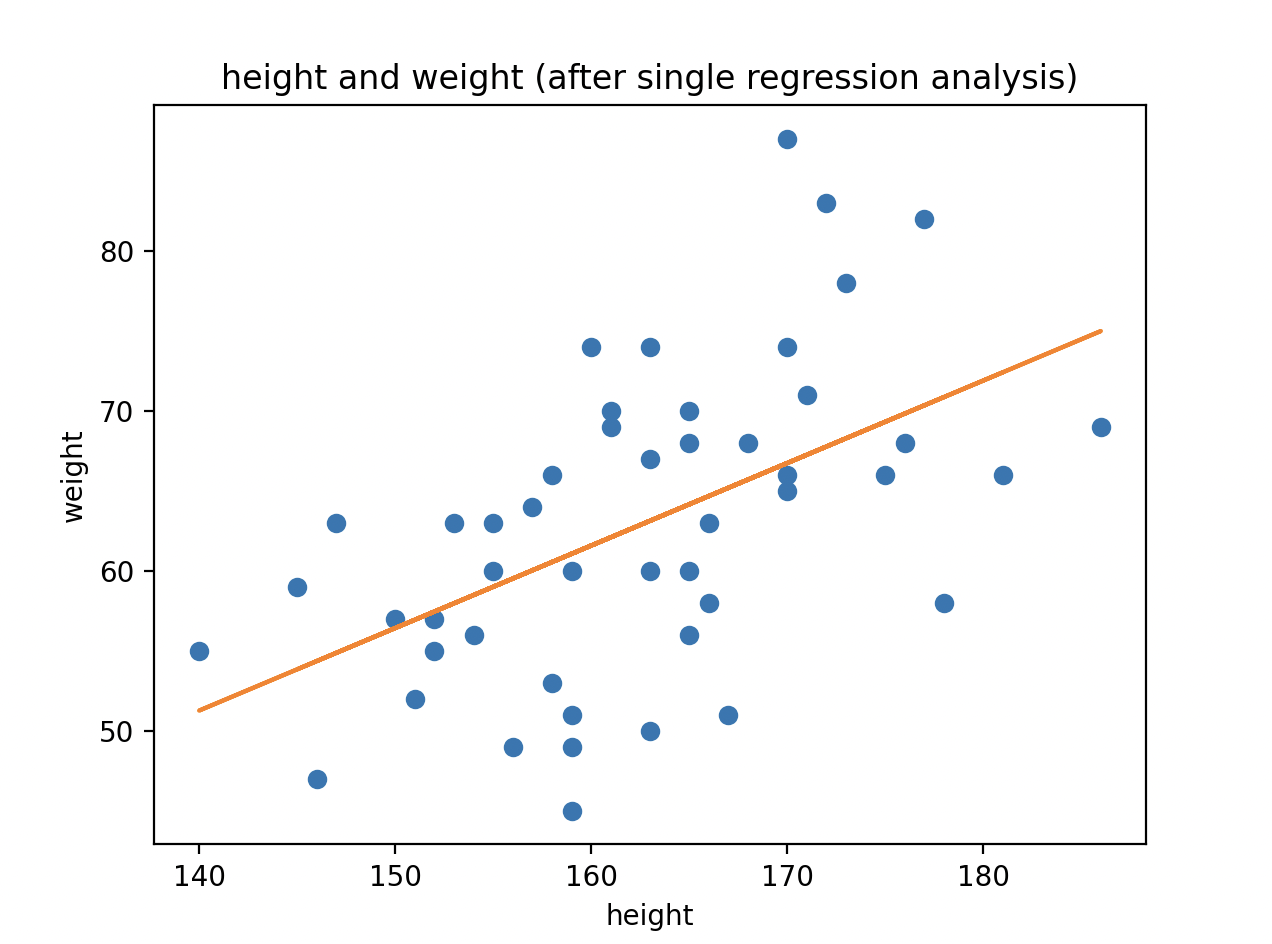
結果は、相関係数は約0.528となりました。また、単回帰での係数と定数はこのようになりました。
$$
Y(体重) = 0.52x(身長) - 20.94(定数)
$$
また、これが因果関係なのかどうかを確かめるための指標の一つとして決定係数があります。
これをみてみると0.279なので非常に当てはまりがいいとは言えません。(データが少ないので)
結果として、3年B組の身長と体重の因果関係はあるかわからないが結論となります。
これは単に相関係数やデータを観測するだけでは得られなかった結論となります。
実装例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
heights = np.array([152, 173, 172, 178, 166, 175, 158, 163, 157, 165, 176, 165, 147, 153, 146, 156, 145, 181, 160, 140, 152, 165, 170, 159,
151, 167, 177, 155, 159, 170, 154, 163, 161, 165, 150, 158, 163, 186, 168, 170, 155, 159, 170, 163, 166, 161, 159, 171])
weights = np.array([57, 78, 83, 58, 63, 66, 66, 74, 64, 68, 68, 60, 63, 63, 47, 49, 59, 66, 74, 55, 55, 56, 65,
51, 52, 51, 82, 63, 45, 66, 56, 60, 70, 70, 57, 53, 67, 69, 68, 74, 60, 49, 87, 50, 58, 69, 60, 71])
# 散布図を描く
plt.plot(heights, weights, 'o')
plt.title("height and weight")
plt.xlabel("height")
plt.ylabel("weight")
plt.show()
# 単回帰分析で使用するために、データを1次元配列に変換する
x = heights.reshape(-1, 1)
y = weights.reshape(-1, 1)
# 単回帰分析を実行する
model = LinearRegression()
model.fit(x, y)
# 回帰直線の式を表示する
print('y = %.2fx + %.2f' % (model.coef_, model.intercept_))
# 回帰直線を描く
plt.plot(x, y, 'o')
plt.plot(x, model.predict(x), linestyle="solid")
plt.title("height and weight (after single regression analysis)")
plt.xlabel("height")
plt.ylabel("weight")
plt.show()
ちなみに、より正確に判断するために統計では重回帰分析や最小二乗法など様々な手法を扱います。それによって単純に考慮することができないような要素を考慮した上で分析をし真の因果関係は何かを見つけ出します。
相関関係と因果関係の違い
因果関係は相関関係も持つため、相関関係に内包された要素であることがわかります。
しかし、相関係数は観測データのみである程度推測できるが、因果関係はデータだけではわからず、先程紹介したような回帰分析やRCT(ランダム化比較試験)を行わないとわからないものです。主に統計ではこの因果関係が成立しているのかどうかを確かめるためにあるのです。
終わりに
ここまで、相関関係と因果関係について説明していきましたがいかがだったでしょうか。
一見、相関関係だけで因果関係が表せそうな気がすると思いますが、実はそんな単純ではなかったことがわかりました。
大学に進学された方なら大体通るであろう「統計学」
いろんな分析手法ばかり学ばされて何の意味があるのだろうか?と疑問に持った方も多いはずです。実は、その裏にはこのような単純な相関関係からでは因果関係を説明できない。色々な事情があったということです。
参考文献
matplotlib で散布図 (Scatter plot) を描く
因果関係と相関関係の違いとは? データ分析によりグロースさせる | グロースマーケティング公式|Growth Marketing
データは語る。相関関係と因果関係で、データにストーリーを持たせよう。 | DIGITAL | オペレーションを進化させる現場のWebマガジン 現場ドリブン