LoginSignup
29
32
@nicklegr(にっくる)

C++の高速なハッシュテーブルの実装を読んだ (ankerl::unordered_dense)

Last updated at Posted at 2023-09-14

C++の高速なハッシュテーブル、ankerl::unordered_dense::{map, set}の実装を読んでみた。

作者によるとabsl::flat_hash_map(通称SwissTable。Google製)と同程度に挿入・検索が速く、特にイテレートはstd::vectorと同等で最速らしい。

Comprehensive C++ Hashmap Benchmarks 2022にベンチマークがある。
(作者自身による計測なので、多少のバイアスはあるかもしれない)

基本のアルゴリズム

Robin Hood hashing + Backward shift deletionを使用している。
まずこれを理解すると分かりやすい。

データ構造

おおよそ、下記のような構造。

struct Bucket {
    uint32_t dist_and_fingerprint;
    uint32_t value_idx;
};

std::vector<Bucket> m_buckets;
std::vector<value_type> m_values;

m_bucketsがハッシュテーブルの管理データで、m_valuesが格納した要素の配列。
m_valuesは全要素が隙間なく詰められていて、イテレートする際はここを直接走査する。

dist_and_fingerprintは、名前の通り2つの値が一つの変数にパックされている。
この工夫で、いろいろと効率よく処理できる(後述)

  • 上位3バイト: dist
    • ハッシュ関数で求めた位置から、実際に要素が格納されている位置までの距離
    • 基本アルゴリズムの解説でProbe Sequence Lengthと呼ばれているものと同じ
    • 1から数えるので注意。つまりdist == 1ならハッシュ関数で求めた位置と実際に格納されている位置が等しい
  • 下位1バイト: fingerprint
    • ハッシュ値の下位1バイトを格納

dist_and_fingerprint == 0の場合はEmpty(その位置に要素が格納されていない)

distを1から数えるのは、fingerprintが0x00の場合にEmptyと区別できるようにするためだと思う。

実装を読む

find

コアの処理はdo_findにある。抜粋してコメントを入れた。

auto mh = mixed_hash(key);
auto dist_and_fingerprint = dist_and_fingerprint_from_hash(mh);
auto bucket_idx = bucket_idx_from_hash(mh);
auto* bucket = &at(m_buckets, bucket_idx);
// ...
while (true) {
    // distとfingerprintが両方等しいか？
    if (dist_and_fingerprint == bucket->m_dist_and_fingerprint) {
        // fingerprintはハッシュ値の下位1バイトなので、これが等しければキーも等しい可能性が高い
        // なので、実際にキーを比較する
        if (m_equal(key, get_key(m_values[bucket->m_value_idx]))) {
            // キーが一致したらその要素を返す
            return begin() + static_cast<difference_type>(bucket->m_value_idx);
        }
    } else if (dist_and_fingerprint > bucket->m_dist_and_fingerprint) {
        // dist > bucket->m_dist なら探索終了。見つからなかったという結果を返す
        // distが等しいときの挙動は後述
        // Emptyの判定も兼ねている(Emptyの場合右辺が0なのでtrue)
        return end();
    }
    // dist++し、次のbucketに進む
    dist_and_fingerprint = dist_inc(dist_and_fingerprint);
    bucket_idx = next(bucket_idx);
    bucket = &at(m_buckets, bucket_idx);
}

基本は普通のRobin Hood hashingと同様に、distが小さいか等しい間リニアサーチを行っている。

加えて、fingerprintが異なるときはキーの比較を省略して、m_valuesにアクセスしないのでキャッシュ効率も良い。
理想的なハッシュ関数では、違うハッシュ値でfingerprintが偶然一致する確率は1/256。
そのため、fingerprintを比較するだけでも十分高い効率で枝刈りができる。
1バイトしか保持しないことでデータがコンパクトで、m_bucketsがキャッシュに乗りやすい。
このあたりはSwissTableを参考にしているのかも。

dist_and_fingerprint > bucket->m_dist_and_fingerprintという式はなかなか巧妙。
基本的にはdistのみを比較している。distが上位3バイトにあるので、両辺のdistの値が異なる場合は、fingerprintの値は影響せずdistのみを比較できる。

両辺のdistが等しいときは、fingerprintの値を比較することになる。
これはどういう意味があるのか、作者に聞いてみた。
要素が見つからなかったとき、探索する要素数が平均で半分になるので効率的らしい。

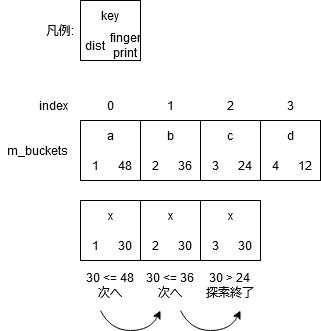
図解すると下記のようになる。
図の状態からkey = xを検索し、index = 0にハッシュされてそこから探索開始したとする。
(実際はm_bucketsにkeyは入っていない。分かりやすくするための注釈)

ankerl_unordered_dense_find.drawio.png

普通のRobin Hood hashingではdistのみを比較するので、key = d以降との比較も必要になるがそれを省略できる。
これを可能にするため、insert処理にも似たような工夫がある。

insert

コアの処理はemplace(Args&&... args)が読みやすい。

// ...

auto& key = get_key(m_values.emplace_back(std::forward<Args>(args)...));
auto hash = mixed_hash(key);
auto dist_and_fingerprint = dist_and_fingerprint_from_hash(hash);
auto bucket_idx = bucket_idx_from_hash(hash);

// dist <= bucket->m_distなら探索を続ける。これは普通のRobin Hood hashingと同じ
// distが等しいときは後述
while (dist_and_fingerprint <= at(m_buckets, bucket_idx).m_dist_and_fingerprint) {
    if (dist_and_fingerprint == at(m_buckets, bucket_idx).m_dist_and_fingerprint &&
        m_equal(key, get_key(m_values[at(m_buckets, bucket_idx).m_value_idx]))) {
        // 既に同じキーの要素があるので挿入しない
        m_values.pop_back();
        return {begin() + static_cast<difference_type>(at(m_buckets, bucket_idx).m_value_idx), false};
    }
    dist_and_fingerprint = dist_inc(dist_and_fingerprint);
    bucket_idx = next(bucket_idx);
}

// 要素を挿入し、その位置より後ろの要素を移動
auto value_idx = static_cast<value_idx_type>(m_values.size() - 1);
place_and_shift_up({dist_and_fingerprint, value_idx}, bucket_idx);

return {begin() + static_cast<difference_type>(value_idx), true};

こちらも、両辺のdistが等しいときに普通のRobin Hood hashingと少し違う。
fingerprintが小さい限り探索を続け、その直後に挿入するので、distが等しいときはfingerprintの値で降順ソートされることになる。

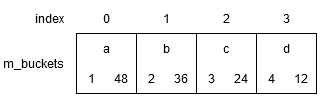
findの例だと、下記の図でkey = a, b, c, dがすべてindex = 0にハッシュされるとしたら、どんな挿入順でも下記の並びになる。

ankerl_unordered_dense_insert.png

結果、findで説明した効率化が可能になる。
fingerprintの比較条件がfindでは>, insertでは<=になっていて対称性がある。

place_and_shift_up()では、要素を挿入し、挿入位置より後ろの要素は無条件に1個ずつ後ろに移動している。
普通のRobin Hood hashingでは、要素を1個ずつ比較してdistを超える位置までスキップするので少し違う。
これは分岐が少なくなることで速くなるのかな？

erase

コアの処理はdo_erase()にある。

auto const value_idx_to_remove = at(m_buckets, bucket_idx).m_value_idx;

// まずBackward shift deletionを行う。これは通常通りの動作
auto next_bucket_idx = next(bucket_idx);
while (at(m_buckets, next_bucket_idx).m_dist_and_fingerprint >= Bucket::dist_inc * 2) {
    at(m_buckets, bucket_idx) = {dist_dec(at(m_buckets, next_bucket_idx).m_dist_and_fingerprint),
                                    at(m_buckets, next_bucket_idx).m_value_idx};
    bucket_idx = std::exchange(next_bucket_idx, next(next_bucket_idx));
}
at(m_buckets, bucket_idx) = {};

// m_valuesを更新
if (value_idx_to_remove != m_values.size() - 1) {
    // 削除するvalueが配列の末尾じゃなかった
    // 末尾の要素を削除するvalueの位置にmoveして上書きする
    auto& val = m_values[value_idx_to_remove];
    val = std::move(m_values.back());

    // moveしたvalueを指していたBucket.m_value_idxを書き換える
    // valueのハッシュを取ってbucketの位置を推定、そこからm_value_idxが一致するものをリニアサーチ
    auto mh = mixed_hash(get_key(val));
    bucket_idx = bucket_idx_from_hash(mh);

    auto const values_idx_back = static_cast<value_idx_type>(m_values.size() - 1);
    while (values_idx_back != at(m_buckets, bucket_idx).m_value_idx) {
        bucket_idx = next(bucket_idx);
    }
  
    // 見つかったのでm_value_idxを更新
    at(m_buckets, bucket_idx).m_value_idx = value_idx_to_remove;
}

// moveした末尾要素を削除
// (最初から末尾要素を削除する場合はmoveは行われない)
m_values.pop_back();

m_dist_and_fingerprint >= Bucket::dist_inc * 2という式が少しトリッキー。
dist_inc == (1 << 8)なので、意味は(dist >= 2 && !Empty)。
distは1から数えるので、dist == 1、つまりハッシュ関数で求めた本来の位置にある要素があったらfalseになる。
またはBucketがEmptyだと値は0なので、その際もfalseになる。
つまり、普通のBackward shift deletionの処理と同じ。

m_valuesの更新では、削除する要素を末尾要素で上書きして、m_valuesの要素に隙間が空かないようにしている。
最初に挙げたイテレートが高速というメリットはこうやって実現している。

ちなみにこのテクニックは汎用的に使えて、vectorで要素の削除が $O(n)$ ではなく $O(1)$ になる。(順序を気にしない場合)
vectorの全要素をイテレートできればよく、インデックスアクセスは不要、という場合に高速化できる。

ハッシュ関数

wyhashをベースにした実装がデフォルトで用意されている。
詳しくは関数オブジェクトの定義やmixed_hash()を参照。

整数型やポインタ型の場合はwyhashの簡易実装を使う。

[[nodiscard]] inline auto hash(uint64_t x) -> uint64_t {
    return detail::wyhash::mix(x, UINT64_C(0x9E3779B97F4A7C15));
}

文字列の場合は通常のwyhashを使う。

ユーザー定義型のハッシュ関数を作る場合、単純な型なら下記のコードでいけるとREADMEに書いてある。
型のメモリ表現をそのままバイト列としてwyhashを求めている。

struct custom_hash_unique_object_representation {
    using is_avalanching = void;

    [[nodiscard]] auto operator()(point const& f) const noexcept -> uint64_t {
        static_assert(std::has_unique_object_representations_v<point>);
        return ankerl::unordered_dense::detail::wyhash::hash(&f, sizeof(f));
    }
};

上記のようにusing is_avalanching = voidが定義されていたら、結果のハッシュ値をそのまま使う。分散がいいハッシュ関数だと宣言する意味がある。
定義されてなければ、結果のハッシュ値をさらにwyhashの簡易実装に通して分散をよくする。

is_avalanchingが定義され、ハッシュ値のサイズが64bitに満たない場合は、ハッシュ値に0x9ddfea08eb382d69を乗算して64bitに拡張される。
元のハッシュ値の分散がよければ、wyhashを通さず簡易処理でいいという判断？

0x9e3779b97f4a7c15や0x9ddfea08eb382d69という定数は、ビットの分散がよくなる値を選んでいるらしい。数学的な根拠はちゃんと理解できなかった。
ちなみに、CityHashの実装の一部に同じ値がある。

まとめ

  • m_valuesに全要素が隙間なく詰められているので、イテレートが高速。というか理論上最速
  • dist_and_fingerprintという巧妙なデータ構造で、高いキャッシュ効率・キーの比較の枝刈り・さらにfindの探索量の削減を一度に達成している
  • ハッシュ関数も高速で分散が良いといわれるwyhashを使用し、さらに整数型の場合に特化した高速化もある

という感じで、シンプルかつとても巧みに設計されている印象を受けた。
特にイテレートが高速なのはハッシュテーブルでは珍しい特徴なので、全要素を頻繁にイテレートする用途には最適だと思う。

29
32
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
29
32