こんにちは、Niaです。
今回は.NET Frameworkの実数型の1つ、decimal型(Decimal型)の加減算の様子を見てみました。
1. decimal型とは
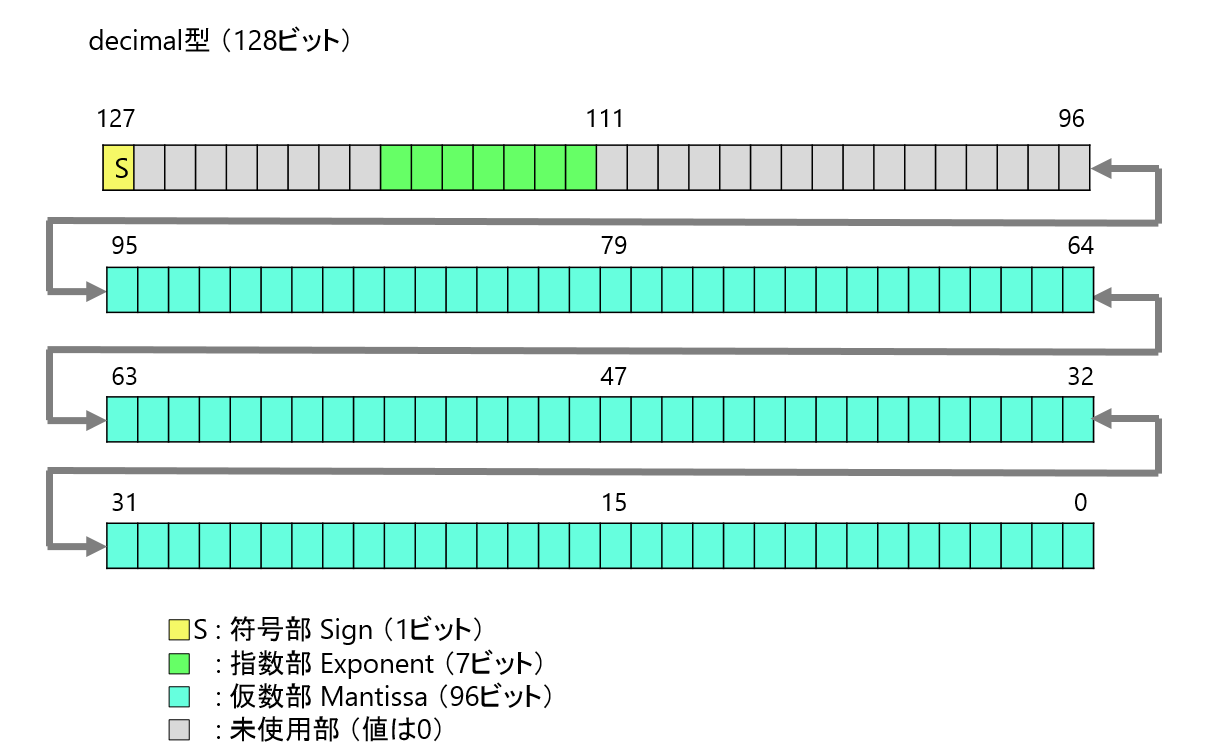
decimal型は1ビットの符号部と7ビットの指数部、96ビットの仮数部で構成された、10進数表現の浮動小数点値です。但し、仮数部は整数として表しており、指数部で小数点の位置を指定します。
decimal型の値 = $(-1)^{[符号部]} \times [仮数部] \times 10^{-[指数部]}$
参考 : Decimal 構造体 | MSDN
https://msdn.microsoft.com/ja-jp/library/system.decimal.aspx
2. decimal型同士の加減算の様子
実際にdecimal型同士の加算の様子を見てみましょう。
using System;
using System.Linq;
class Program {
static void Main( string[] args ) {
decimal d1, d2, d3;
d1 = 1024m;
d2 = 0.2048m;
d3 = d1 + d2;
DecimalUnit d1Unit = new DecimalUnit( d1 ),
d2Unit = new DecimalUnit( d2 ),
d3Unit = new DecimalUnit( d3 );
Console.WriteLine( "d1 : " );
d1Unit.ViewInfo();
Console.WriteLine( "d2 : " );
d2Unit.ViewInfo();
Console.WriteLine( "d3 = d1 + d2 : " );
d3Unit.ViewInfo();
}
}
// decimal型の値から符号部、指数部、仮数部の値を求めます。
struct DecimalUnit {
private decimal org; // 元の値
public bool Sign; // 指数部
public int Scale; // 指数部
public int[] Part; // 仮数部
public DecimalUnit( decimal d ) {
org = d;
// decimal型の内部表現の値はGetBitsメソッドで取得します。
int[] ds = decimal.GetBits( d );
// 符号部は4番目の要素の最上位1ビットです
Sign = ds[3] >> 31 != 0;
// 指数部は4番目の要素の下位17~24ビット目( 7ビット分 )です。
Scale = ( ds[3] >> 16 ) & 0x7F;
// 1~3番目の要素は仮数部( 96ビット整数 )です。
Part = ds.Take( 3 ).ToArray();
}
// 情報をコンソール画面に出力します。
public void ViewInfo() {
Console.WriteLine( "値 : {0:G}", org );
Console.WriteLine( "バイナリ値 : {0}", string.Join( " | ", decimal.GetBits( org ).Reverse().Select( b => string.Join( " ", BitConverter.GetBytes( b ).Reverse().Select( b2 => string.Format( "{0:X2}", b2 ) ) ) ) ) );
Console.WriteLine( "符号部 : {0}", Sign );
Console.WriteLine( "指数部 : {0}", Scale );
// decimal型はint型やlong型など整数型の上位互換なので、
// 指数部を0にすれば、仮数部の値を求めることができます。
Console.WriteLine( "仮数部 : {0:F0}", new Decimal( Part[0], Part[1], Part[2], false, 0 ) );
Console.WriteLine();
}
}
実行結果
d1 :
値 : 1024
バイナリ値 : 00 00 00 00 | 00 00 00 00 | 00 00 00 00 | 00 00 04 00
符号部 : False
指数部 : 0
仮数部 : 1024
d2 :
値 : 0.2048
バイナリ値 : 00 04 00 00 | 00 00 00 00 | 00 00 00 00 | 00 00 08 00
符号部 : False
指数部 : 4
仮数部 : 2048
d3 = d1 + d2 :
値 : 1024.2048
バイナリ値 : 00 04 00 00 | 00 00 00 00 | 00 00 00 00 | 00 9C 48 00
符号部 : False
指数部 : 4
仮数部 : 10242048
指数部の値から d1(仮数部 = 1024, 指数部 = 0)と d2( 仮数部= 2048, 指数部 = 4)の加算の場合、d1の指数部を 4 にして仮数部に $10^4$ を掛けてから、仮数部同士で加算していることがわかります(※10240000の16進数は 0x9C4000 です)。
つまり、decimal型同士の加減算は以下のように行われます。
- 指数部を比較し、指数部の小さい実数の仮数部を指数部の大きい実数の指数部(すなわち小数部の精度が大きい方)に合わせて指数部の値を増やし、その分だけ10のべき乗を掛けます。
- 仮数部同士で加減算をします。
3. decimal型での情報落ち
もし、decimal型で極端に大きな値と極端に小さな値の加算を行ったらどうなるのでしょう。
先ほどのプログラム「decimal-add.cs」にて、d1とd2を以下の値に設定し、実行してみましょう。
// 仮数部の上位32ビットを「0xFFFF / 100」とし、指数部と符号部を0とします。
d1 = new decimal( 0, 0, int.MaxValue / 100, false, 0 );
// 指数部が10になるように、小数点以下10桁の値を代入します。
d2 = 0.0123456789m;
実行結果
d1 :
値 : 396140803716884532587134976
バイナリ値 : 00 00 00 00 | 01 47 AE 14 | 00 00 00 00 | 00 00 00 00
符号部 : False
指数部 : 0
整数部 : 396140803716884532587134976
d2 :
値 : 0.0123456789
バイナリ値 : 00 0A 00 00 | 00 00 00 00 | 00 00 00 00 | 07 5B CD 15
符号部 : False
指数部 : 10
整数部 : 123456789
d3 = d1 + d2 :
値 : 396140803716884532587134976.01
バイナリ値 : 00 02 00 00 | 7F FF FF D0 | 00 00 00 00 | 00 00 00 01
符号部 : False
指数部 : 2
整数部 : 39614080371688453258713497601
d1の指数部が0、d2の指数部が10なので、それらの和であるd3の指数部は10になると思いきや、この結果では2になりました。
実はdecimal型で指数部に合わせて仮数部を調節する時、仮数部が表現可能な値の範囲を超えてしまう(オーバーフローする)場合、ギリギリ超えないところまで10のべき乗をかけ、それに合わせて指数部の値を調整します。その後、もう一方の指数部を先ほどの指数部に合わせて減らし、その分だけ10のべき乗で割ります。
例えば、先ほどのd1、d2の場合、d1の指数部が0、d2の指数部が10なので、d1の仮数部に $10^{10}$ を掛けますが、値の範囲を超えない最大の10のべき乗は $10^{2}$ なので、d1の指数部を2だけ増やし、仮数部に $10^{2}$ を掛けます。d2の指数部は調整したd1の指数部に合わせて2に設定し、それに合わせて仮数部を $10^8$ で割ります。これによって、d2の小数点以下第3位以降は切り捨てられてしまいます。
表現可能な値の範囲に気を付けてプログラミングしていきましょう。
それでは、See you next time!