回路があなたに意味を与えるのではない｡ あなたが回路に意味を与える｡
ぬくぬく当番
多入力AND、OR
最初に論理回路の多入力について軽く解説しておきます。
AND、ORの動作を言い換えると
・ANDは、入力が全て1の時だけ1
・ORは、入力のうち1つでも1なら1
という事です。入力が増えたら下のように追加していきます。
3入力（A,B,C）のAND=(A AND B) AND C
3入力（A,B,C）のOR=(A OR B) OR C
4入力（A,B,C,D）のAND=((A AND B) AND C) AND D
...
※これは多入力の場合についてです。多桁の場合とは違いますから、注意してください。
入力の組み合わせと出力と論理回路
今回はゲートを組み合わせて目的に合った回路を作る方法についてです。
どんな複雑な回路でも基本要素のAND,OR,NOTで作れる、という説明を見かけた事があると思います。複雑かどうか置いといて、例えば入力が2つの場合、入力の組み合わせは {0,0},{0,1},{1,0},{1,1} の4通りです。
この4通りのそれぞれについて、0と1のどちらを出力するのか、これは回路を設計する人が自由に選ぶことが出来ます。
入力が2つの場合、4つの出力のそれぞれについて0か1かを決めるとして、組み合わせの種類は2^4で16種類、つまり入力2つの回路のバリエーションは16種類という事です。16種類のどれであっても同じ手法で回路にする事が出来ます。
では、どうやるのか
まず出力が1の組み合わせに注目します。2つの入力それぞれについて、入力の条件が0の時は反転、1の時はそのままの信号をANDに入力します。
出力が1の組み合わせのAND演算後の信号が揃ったら、それを全部1つのORに入れます。1
これだけでは解りにくいので実際にやってみましょう。
XOR
論理演算のXOR（EXORとも言う）を例に順を追って説明します。
2入力のXORは、2つの入力が違う場合は出力が1、同じなら出力が0です。排他的論理和とか Exclusive OR とかいいます。
ORは入力が両方1でも1を出力しますがXORは両方1の時は0を出力します。ORは「かにぱん？アンパン？」のような時で「両方食べる」もアリだけど、XORは「私？あの娘？」の時に似ています。XORはどちらか片方だけ1なら1、両方選ぶと修羅場になって結果何も手に入らないから0の「排他的なOR」です。
ではまず表にしてみましょう。
| IN1 | IN2 | OUT |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| IN1とIN2が違っている場合というのは、{IN1,INT2}が{0,1}と{1,0}の場合ですね。それ以外は出力0です。 |
※こういう、入力の組み合わせと対応する出力をまとめた表を真理値表と言います。
これを基本ゲートを組み合わせた論理回路にしてみましょう。
・出力が1の場合に注目します。二行目と三行目が出力1です。
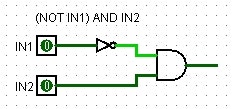
・二行目 IN1=0 IN2=1 の場合がOUT=1です。IN1が0の場合は(NOT IN1)が1の場合ですから、二行目は
((NOT IN1) AND IN2)ならOUT=1
と言い換える事ができます。
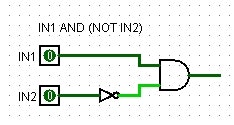
・三行目 IN1が1でIN2が0の場合もOUTが1です。IN2が0という事は、NOT IN2が1の場合という事です。
(IN1 AND (NOT IN2))=1が成立する時もOUT=1です。
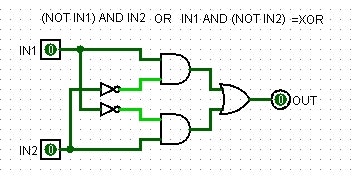
・二行目か三行目の条件、どちらかが成立する場合、といえばORですね。この表は
((NOT IN1) AND IN2)
OR
(IN1 AND (NOT IN2))
を出力する回路になります。
どちらも成立しないなら、一行目か四行目の場合なのでORが0を出力します。
そしたらこの2つをORでまとめます。
※論理演算ではORよりANDの方が優先順位が高いことに注意してください。
A OR B AND C は、B AND C を先に処理します。
ココまで大事です、よいですか？
入力がどんなに増えてもこの手法はそのまま使えますから、「どんなに複雑な」ものでも作れるという事になります。
積と和
論理演算ではORよりANDの方が優先順位が高い事は↑に書きました。
また、ORやANDは、交換則が成立します。
A OR B と B OR A は結果が同じになります。ANDも同様です。
この事から OR、ANDを四則演算の加算と乗算にみたてて、ORを「和」、ANDを「積」と言い換える事があります。
最適化
下のような場合を考えてみましょう。
| IN1 | IN2 | OUT |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
まず、出力が1の組み合わせに注目…しなくてもこれは、IN1に関係なくIN2を出力すればいいですね。
OUT=1は{IN1,IN2}={0,1},{1,1}、言い換えるとIN2が1のときはIN1に関係なくOUTは1です。
それ以外の時はOUTは0ですから、この表は
OUT=IN2
です。
入力が増えて表が大きくなったら、こういった単純化できる組み合わせは見つけにくくなります。最適化については詳しく解説しませんが、最適化の手法や論理的な話、最適化の数学的根拠など、興味があったら[カルノー図]とか[QM法]とか[ド・モルガン]とかで[検索←]してみてください。
※カルノー図は最適化の手法であって、理解していないと回路が設計出来ないというわけではありません。
サンプル：ハミング重み
入力が増えて表が大きくなった時の例として、4入力のハミング重み回路を作ってみましょう。
ハミング重みとは、0とのハミング距離で、簡単に言うと二進数で表した時の1の数です。下の表のA～Dは二進数で十進数の0~15に対応しています。Y2～Y0は五進数の0～4に対応しています。
| A | B | C | D | → | Y2 | Y1 | Y0 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
出力が複数の時は、それぞれの出力を別々に考えて回路を組みます。
結果だけちらっと。QM法と呼ばれている方法で最適化してありますが、最適化しなくてもあまり変わらないです。
この表の出力Y1は1の場合より0の場合の方が少ないですから、Y1の演算は出力を反転してから回路を作成し、Y1の出力をさらに反転する最適化もあります。
また、Y0はA==Bの時 C XOR D、A!=Bの時 NOT(C XOR D) ですから、そういう最適化もあるでしょう。トライしてみてください。
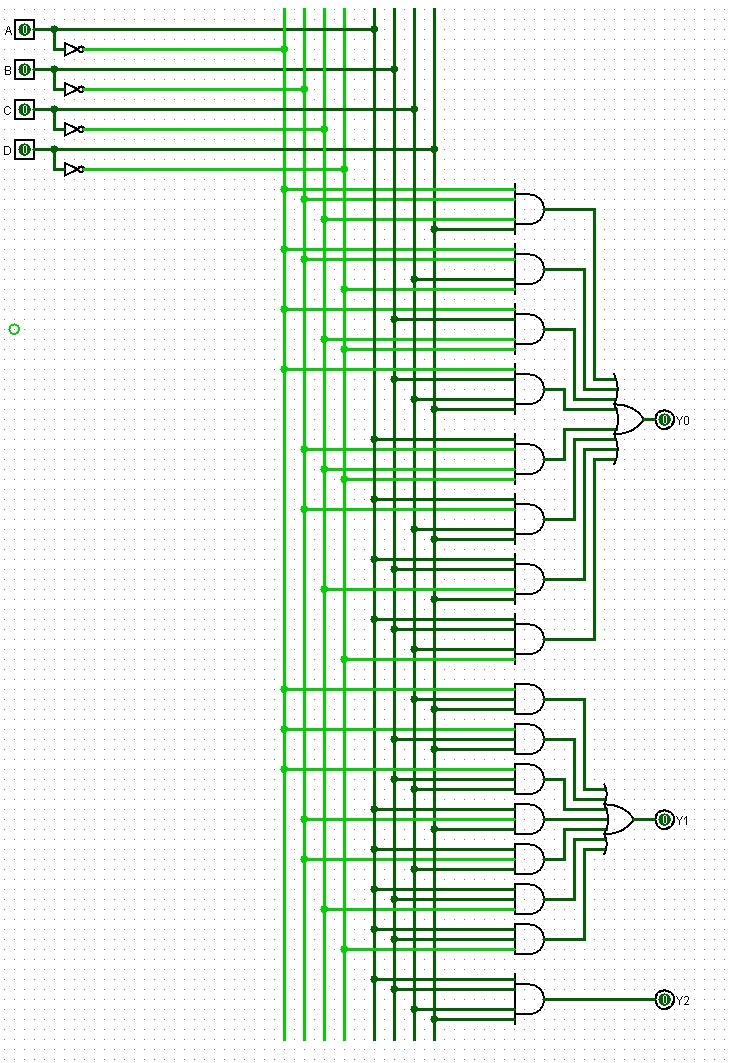この回路は、NOT、AND、ORの基本要素と呼ばれる論理GATE、それから配線で出来ています。論理GATEについては前回MOSFETで作りました。MOSFETだけで出来た回路です。しかし、この回路には「ハミング重み」という意味があります。
ここ、大事なところです。続きはまた。
次回は算術演算の話です。
※以上の回路は GATE2CIRCUIT.circ に入っています。 Logisim用のドキュメントです。xmlですから右クリック推奨。
一覧へ
-
これはプロダクトタームとか主加法標準形といいます。 ↩