コンピュータの動作原理（２）論理GATEを作る ーMOSFETの動作ー

今回はMOSFETから論理GATEと呼ばれる基本要素を作るまでの解説です。

なぜ二進数か？

アナログとデジタルについてと二進数については、よく出来てる解説がたくさんありますからそちらを見てください。コンピュータの動作原理について知ろうとする意欲のあるひとなら既に理解していると思います。たぶんこれを読んでいる人なら、二進数で011+001は？すぐに100って浮かんでくるでしょう。

ところで、二値を扱う事と二進数とは直接関係がありません。
例えばENIACは10組の真空管のうちどれがONになっているかで10進数を表しました。つまり二値十進コンピュータだったわけです。
二進数が採用されたのはその後のEDSACからです。

そもそもなぜ二値なのか？

それは、二値を扱う論理が出来上がっている事、トランジスタのスイッチングの状態が電気的に見てON/OFFの２種類である事の２つが大きな理由として挙げられるでしょう¹。

0と1だけを要素に持つ集合はブール代数の成り立つ典型的な例です、演算の結果に紛れがありません。二値だと0の論理否定（0ではないモノ）は1だけで、1で無いものもまた、0だけです。

今日のコンピュータの数学的裏づけは、ジョージ・ブールの理論をクロード・シャノンが電気回路で実現可能であることを論文にまとめた事にあります。

また、コンピュータを構成する最も基本的な要素、トランジスタの状態はON/OFFの2種類です²。
シャノンは電気回路（電磁リレー）でブール代数が実現できることを示しました。これがその後、リレーから真空管、そしてバイポーラトランジスタ、MOSFETとデバイスが変っても、スイッチングという特徴が変らなければシャノンの論理がそのまま使えるわけです。

トランジスタの動作原理は物理学の領域になるので、コンピュータの動作原理を考える時トランジスタが最もプリミティブな要素という事になります。これからここを出発点にして、コンピュータの動作原理を解説していきます。

　※より物理学寄りの事が知りたい人は、たとえば「半導体プロセスまるわかり　デジタル回路を構成するトランジスタ」がお勧めです。

電圧と電流について

トランジスタの話の前に電圧と電流についてすこし。
まず２つ。

1. 電圧は負荷の両端に発生する
2. 電圧と負荷が決まれば、イヤでも流れる電流は決まる。

1で言う「負荷」は無限大でもかまいません。電池の＋と－の間をテスターで測ればだいたい1.5Vですよね。電池の両端の間には1.5Vの電圧が「発生」しているって事です。回路のどこかに電源があれば、電流が流れていなくても電圧は発生しています。
2は電圧が発生している２点間を負荷でつないだ場合です。電圧と負荷で流れる電流は決まります。
負荷と言うのは抵抗であったり発光であったり動力であったりいろいろですが、このシリーズの範囲では抵抗と考えていいでしょう。

それから電圧について。
電圧は抵抗を使って下げる事が出来ます。電源とGND（グランド、グラウンドとも、電源のマイナス極）の間に抵抗を二つ直列に入れると、その２つの抵抗の間の電圧は、２つの抵抗の値の割合に応じて低くなります。分圧といいます。
例えば

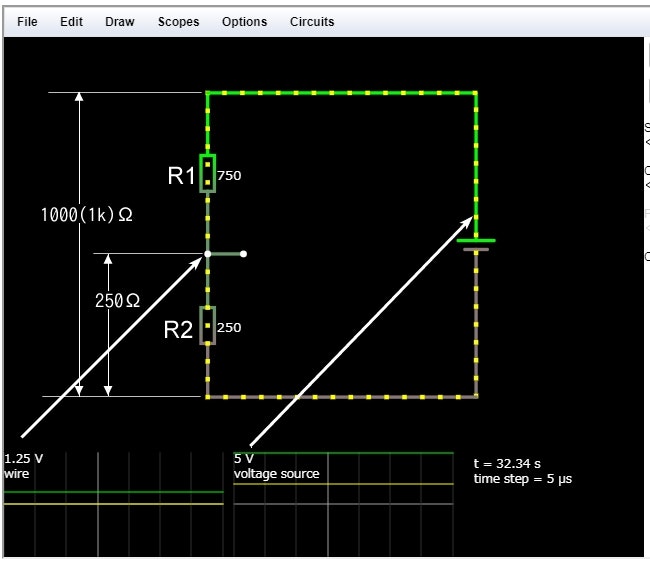
電源は５V、電源とGNDの間に750Ωの抵抗(R1)と250Ωの抵抗(R2)を入れました、電源とGNDの間は1KΩ、R1とR2の間とGNDの間は250Ωですから、抵抗の比は4:1、電圧も同じ比率で1.25Vです。

MOSFET

MOSFETはトランジスタの一種で２端子間のON/OFF（電気的につながっている/つながっていない）を3つ目の端子の電圧でコントロールする素子です。
以下のような記号で表します³。

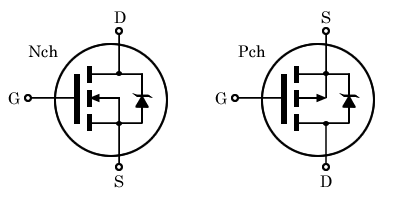
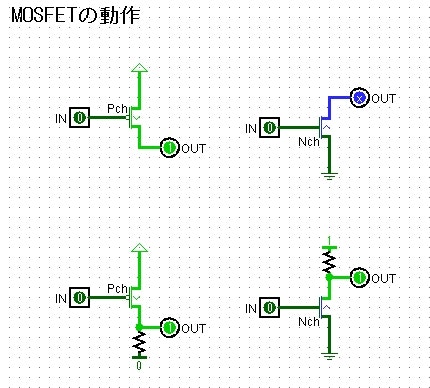
Nch（エヌチャンネル）はD(ドレイン）からS（ソース）の方向に向かう電流の制御に使います。G(ゲート）に電圧を掛けると、D→Sに電気が流れるようにスイッチがONになります。Nchは通常SをGNDにつなぐので、SとGの間の電圧で制御します。
Pch（ピーチャンネル）は２つの意味でその逆です。まず、制御できる電流の方向がS→Dです。そしてGに電圧が掛かっている間はスイッチがOFFです。Pchは通常Sを電源につなぎますから、OFFにする時はGも電源につなぎます。ONにする時はGをSより充分電圧の低いどこか（通常GND）につなぎます。

図にすると↓のような動作で、どちらも電圧がかかっていない状態です。Gに電圧をかけるのは、下図の矢印の方向に押す（圧力をかける）事と考えてください。電圧ですし。

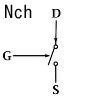
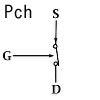
MOSFETは電圧で制御するので、GからD又はGからSへ電流が流れている必要はありませんし、実際流れないように出来ています。Gの電圧を電源かGNDかどちらか一方と同じにしてあればMOSFETはONかOFFの状態で安定します。

実物はこんな感じ。

左が「トランジスタといえばこれだよね」っていう3本足のパッケージで、FAIRCHILDの2N7000という型番の物。右は表面実装用でやはりFAIRCHILDのBSS138という型番の製品で、どちらもNchMOSFETです。

MOSFETの電気的動作

MOSFETの電気的な動作の確認です。LogisimでMOSFETの動作を確認します。

それぞれの上段は、PchのSを電源につないでDは何もつないでいない状態（開放という言い方があります）、NchはSをGNDにつないでDは開放です。このままだとスイッチOFFの時の動作が決定できないので、下段のPchはDを抵抗を挟んでGNDに、Nchは抵抗を挟んで電源につないであります。抵抗はMOSFETがONになった時に電源とGNDがショートしないために入れます。
入力が0というのは入力をGNDにつないでいるのと同じ、入力1は電源につないでいるのと同じ状態です。

図にIN、OUTという表記が出てきます。この回路をコントロールしている方に向いている側がINで、他の回路のOUTや電源がつながっていれば0か1かのどちらかになります。
この回路でコントロールするのがOUTです。OUTはその先の回路の制御に使えます。INかOUTかは電流の向きとは関係ありません。

入力が0の時

PchはON、NchはOFFです。

入力が1の時

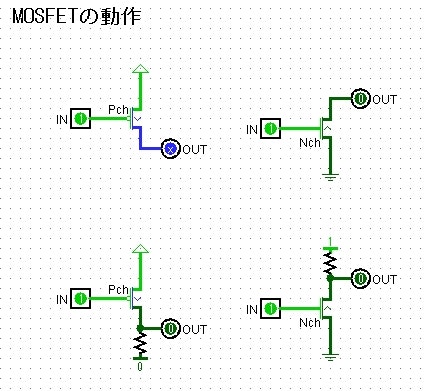
PchはOFF、NchはONです。
入力が反転されて出力側に出ていることが解ると思います。

　※左下、入力は1ですが、Gから他の端子（DかS）には電流が流れないように出来ている（つまり、絶縁されている）ので、入力の1が出力に出て行くことはありません。
　※抵抗を挟んでありますが、電源と直接つながっている所は抵抗0です。なので分圧された結果電源と同じ電圧になります。「入力が0の場合」の左下、出力が1の所がそうです。GNDの場合も同様に考える事が出来ます。

論理GATEとは

論理GATEとは1ビット同士の論理演算が電気的に行える素子です。論理GATEはMOSFETの組み合わせで作れます。
1ビット同士の論理演算ですからC言語でいうと&,|,^,~などです。C言語で a&=0x80; と書いたとします。このAND演算はプロセッサの最もプリミティブな層でMOSFETで出来た素子によって処理されています。8ビットプロセッサならANDのための論理GATEが8こ並んでいて、それぞれが同時に演算をするように出来ています。⁴

論理演算についておさらいしておきましょう。

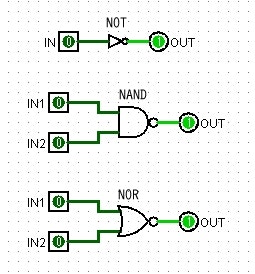
• NOT　入力の否定、反転です。入力が0なら結果は1、入力が1なら0になります。
• AND　2つの入力が両方とも1の時だけ結果が1、それ以外は0です。
• OR　2つの入力のどちらか一方でも1なら1、両方とも0なら結果は0です。

これらが論理演算の基本要素と呼ばれるものです。

MOSFETで論理GATE

MOSFETで作る場合一番シンプルなのはNOTで、これはNchMOSFETが1個で作れます。

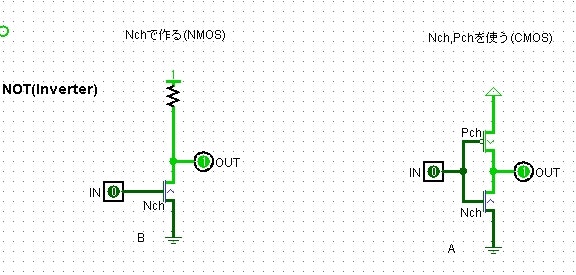
左がNchを1個で作った場合でNMOSと呼ばれている方法です。電源とMOSFETの間に抵抗を入れるので、出力が0の時に電力を消費します。また出力側の電圧の立ち上がりが遅いという弱点があります。
右にあるのがPchとNchを組み合わせた方法でCMOSと呼びます。NchとPchは動作が逆なので、入力が0の時はPchだけ、1の時はNchだけONになります。MOSFETを2個使うので部品が増えますが、NMOSと違って電流が流れ続ける事がないので（OUTを別の回路のINに繋いだ場合）消費電力がNMOSより少なくて済みます。また、出力を1にするための電圧を抵抗ではなくスイッチで制御するので、反応速度の点でもNMOSより有利です。
論理GATEのNOTはInverterとも言います。

では、2個使ったら？

MOSFETを1こだけ使った回路の次は、MOSFETを2こ、直列と並列に並べた場合を考えてみましょう。
話をシンプルにするためにNMOSで作ってあります。

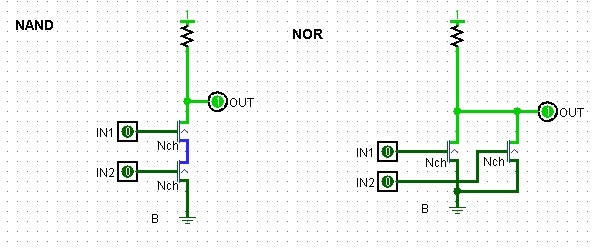
左が2個直列にした場合、右が並列の場合です。
左は2つの入力の両方が1の時だけ0を出力、それ以外は1を出力します。丁度ANDとは出力が逆です。これはNANDと呼ばれる論理GATEです。
右は2つ並列の場合、ORと逆なのでNORと呼ばれます。

NOTも含めて、回路図では下図のような記号で表します。

基本要素

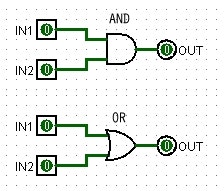
NOTは既に出てきたので、基本要素のANDとORをMOSFETで作ってみましょう。
NANDはANDの出力を反転、NORはORの出力を反転したものですから、ぞれぞれもう一度反転してあげます。
NMOSで作ると以下のようになります。

回路図の記号は以下の通り。

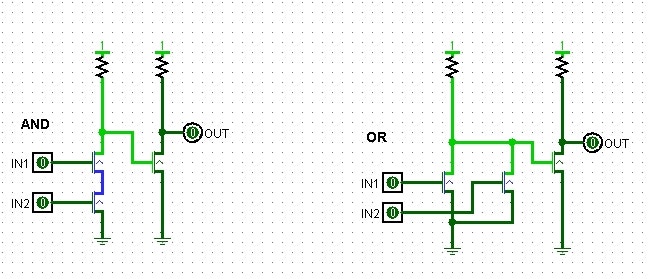
次回はこれら論理GATEを組み合わせていくつか論理回路を作ってみます。

---

　※以上の回路は　FET2GATE.circ　に入っています。 Logisim用のドキュメントです。xmlですから右クリックから保存してください。
　※基本要素のAND、OR、NOTは、上のNANDもしくはNORのどちらか一方だけを組み合わせて作ることが出来ます。これについては論理回路の解説を探せばだいたい出てます。↑の回路図の中に入れてありますので、興味があったら見てください。

一覧へ

コンピュータの動作原理

1. 二進数はメディアへの記録や通信などに都合が良いです。これについてはまた別の話で。 ↩

2. 前回触れましたが、ここでいうトランジスタはMOSFETのようにスイッチング素子として利用されるものを指します。 ↩

3. この記号に含まれているダイオードは回路図の時には省略します。寄生ダイオードと言って、構造上どうしても出来てしまうダイオードです。MOSFETは逆向きの電流（Nchの場合ならDよりもSの電圧が高い場合）はダダ漏れになっています。だからそういう使い方（逆に電圧をかけるような事）はしちゃダメです。 ↩

4. 設計にもよります。Z80のように8ビットプロセッサで4ビットの演算を2回に分けて行う物もあります。 ↩