CADDi Advent Calendar 24 日目の記事です。昨日は 844844 さんによる「React + Neo4j によるコストモデル可視化の取り組み紹介」についての記事でした。明日はついに最終日、我らが TargaMerlin さんによる「whasm!("Rust Christmas")」です!
さて、メリークリスマス。棒読み。クリスマスといえば良い子の皆様がサンタさんからクリスマスプレゼントといただけるという、お子様方にとっては祭事の中でも最も外せない行事ですね。
ところで良い子の方々ばかりずるくありませんか!?
ええ、皆さんは良い子ですからご存じないかもしれないのですが、聞くところによるとこの一年悪さをしてきた悪い子の皆様には、クリスマスプレゼントならぬ、クリスマスペナルティが待っているという噂なのです!! こわいですね。(私は良い子なので存じ上げないのですが。)
コンテンツ
- 罰金付きスケジューリング問題とは
- マトロイドとは
- 一体どういう関係が…?
- 貪欲戦略が重み付きマトロイド上の最大重み独立集合問題の最適解を与えることの証明
- 罰金付きスケジューリング問題から作られるなにかがマトロイドになること、したがってこちらも貪欲戦略で解けること
- ところで間に合うかどうかってどのように判定するのですか?
- 互いに素な集合の森(union-find)を用いて罰金付きスケジューリング問題(ソート済み)を $\Theta ( n \alpha ( n ) )$ で解きます。
記号
あまり変な記号は使わないので飛ばしていただいてもです。
- $A = B \sqcup C$: $B$ と $C$ が非交叉であり、$A$ は $B$ と $C$ の合併集合です。
- 有限集合 $A$ に対して、$\lvert A \rvert$: $A$ の要素数です。
- $A \subseteq B$: $A$ が $B$ の部分集合です。
1 - 罰金付きスケジューリング問題とは
$1$ 単位時間かかるタスクが $n$ 個あり、$1$ から $n$ の番号がついています。それぞれに期限 $d _ i$ と罰金 $w _ i$ が設定されています。いまからタスクの実行順を決めて、期限を過ぎたタスクの罰金の総和をこの実行順序のコストであると定義して、これを最小化しましょうという問題です。
ただし入力 $(n, d, w)$ は
$$
1 \le d _ i \le n, \ 0 \le w _ i \ ( 1 \le i \le n )
$$
を満たすとします。またタスクの実行順を決めてタスク $i \ ( 1 \le i \le n )$ が時刻 $a _ i$ に行われるとことになったとき、これが期限内に終わるとは $a _ i \le d _ i$ を満たすこと、期限を過ぎるとはこれに違反することをいうとします。
答えを知りたい方はこちらです。
期限の遅い順に見ていき、間に合うギリギリの時刻に割り振る、もしくはどうしても間に合わないならば罰金をお支払いすることを受け入れると良いです。
2 - マトロイドとは
Wikipedia だいすきクラブの皆様はこちらです。
こちらです。
ながたかなだいすきクラブの皆様はこちらです。
仕方がないですね〜〜
定義
有限集合 $S$ があるとして、$S$ 上のマトロイドを定義しましょう。
$S$ の部分集合族 $E$ であって、
- $\emptyset \in E$
- $A \in E, B \subseteq A \Rightarrow B \in E$
- $A, B \in E, \ \lvert A \rvert < \lvert B \rvert \Rightarrow \exists x \in B \setminus A, A \cup \lbrace x \rbrace \in E$ (交換性 といいます。)
を満たすものをマトロイドといいます。$(S, E)$ がマトロイドですということも多いです。
マトロイド用語玉手箱のコーナーです。
まずは日本語が得意なので日本語の講義をしていきたいと思うのですが、$E$ に属する集合をこのマトロイドにおける独立集合、そうでないものを従属集合であるといいいます。そして、極大の独立集合を基、極小の従属集合をサーキットといいます。
マトロイドの例
ベクトルマトロイド
$S$ が線形空間の中の有限集合、$E$ がその部分集合のうち線形独立なもの全体の集合であるとき、$E$ は $S$ 上のマトロイドです。つまり、線形独立なものが独立集合なわけですね。
閉路マトロイド
有限グラフを考えて、$S$ がその辺全体の集合、$E$ がその閉路のない部分グラフに対応する辺集合全体の集合であるとき、$E$ は $S$ 上のマトロイドです。つまり閉路を含むものが従属集合なわけですね。とくに単純閉路がサーキットに対応します。(グラフ理論のサーキットは頂点素でなくてもよいので若干ずれていますが、似ていますね。)
メトロイド
1986年8月6日に任天堂から発売されたファミリーコンピュータ ディスクシステム用ゲームソフト。ジャンルはアクションゲーム。任天堂によるディスクシステム専用ソフト第5弾で、『メトロイドシリーズ』の1作目だそうです。
罰金付きスケジューリング問題におけるマトロイド
$S$ がタスク全体の集合、$E$ がタスクの集合のうち「適切な順番で処理するとすべて期限内に処理できるもの」全体の集合とすると、$E$ は $S$ 上のマトロイドとなります。
……本当ですか!?
けっこう非自明なのであとで証明していこうと思います。
マトロイドと貪欲戦略
$(S, E)$ がマトロイドで、$w$ が非負実数値を取る $S$ 上の関数であるとし、これを重みと呼びます。このとき $S$ の部分集合の重みはそれに属する重みの総和 $w ( A ) = \sum _ { x \in A } w ( x )$ であると定義し、$A \in E$ に関する $w(A)$ の最大値と、最大を取る $A$ を求めるという問題を考えます。これを「重み付きマトロイド上の最大重み独立集合問題」と呼びましょう。
重み付きマトロイド上の最大重み独立集合問題における貪欲戦略
重みの大きい順に見ていって、独立性を破壊しないならば追加、破壊するならばスキップを繰り返すと、実は最適解になっています。これから証明していきましょう!
3 - 一体どういう関係が?
罰金が重みと思うとまさにこれです。
というわけで、あとはこれが本当にマトロイドであることと、重み付きマトロイド上の最大重み独立集合問題において貪欲戦略が最適解を与えることを証明すると良いです。勘の良い方ならばわかるかもしれないのですが、さんざん定義を並べて振り回しているだけで、まだ何一つ証明していません。悲しいですね。
4 - 貪欲戦略が重み付きマトロイド上の最大重み独立集合問題の最適解を与えることの証明
やっと証明らしい証明のセクションです。ええ、マトロイドだからと恐れることはありません。いつも通りやるだけです。貪欲戦略の正当性といえばこちらのおふたつを目標にするのが筋が良いです。
- 貪欲選択性:「貪欲に」選んでも最適解への道が閉ざされないことと、
- 部分構造最適性: 「貪欲に」選んだあとで、小さな問題に帰着されていて、それの最適解ともとの問題の最適解が対応していることです。
このうち「部分構造最適性」というのは、動的計画法(DP, dynamic programming)や分割統治法の正当性の証明にも使われることが多いです。
補題 4 - 1: 貪欲戦略が重み付きマトロイド上の最大重み独立集合問題の「貪欲選択性」
$(S, E, w)$ が重み付きマトロイドであり、$x \in S$ は一点集合 $\lbrace x \rbrace$ が独立集合になるような $x \in S$ の中で重みが最大であるものとします。このとき $(S, E, w)$ の最大重み独立集合であって、$x$ を含むものが存在します。
[証明] マトロイドの定義から $E$ は非空なので最大重み独立集合 $B$ がとれます。$k = \lvert B \rvert$ とおいて、$S$ の部分集合 $A _ 1, \dots, A _ k$ を次のように定義すると、これらはすべて独立集合です:
$$
A _ 1 = \lbrace { x \rbrace }, \quad
A _ { i + 1 } = A _ i \cup \lbrace { y _ i \rbrace } \ ( 1 \le i ).
$$
(ただし $y _ i$ は $B \setminus A _ { i }$ の要素であって、上記のように定義した $A _ i$ が独立集合になるものです。これは交換性公理から存在が保証されます。)したがって、$A _ k$ は独立集合です。
さらに $A _ k$ の重みが $B$ の重みと等しいことを証明しましょう。まず、$A _ k$ と $B$ がともに $k$ 元集合で、少なくとも $k - 1$ 個の要素を共有していることに注意すると、$S$ の部分集合 $C$ と $S$ の要素 $y$ を用いて次のように書けます:
$$
A _ i = C \sqcup \lbrace x \rbrace, \quad
B = C \sqcup \lbrace y \rbrace.
$$
従って $x$ の重み最大性より $w ( A ) = w ( C ) + w ( x ) \ge w ( C ) + w ( y ) = w ( B )$ となりますが、$B$ は最大重み独立集合でしたから $w ( A ) \le w ( B )$ となり、$w ( A ) = w ( B )$ が従います。よって $A$ も最大重み独立集合です。∎
補題 4 - 2: 貪欲戦略が重み付きマトロイド上の最大重み独立集合問題の「部分構造最適性」
$\mathcal M = (S, E, w)$ が重み付きマトロイドであり、$x$ は $\lbrace x \rbrace$ が独立集合であるような $S$ の要素であるとします。このとき、$\mathcal M _ x = (S _ x, E _ x, w _ x), \mathcal M ^ x = (S ^ x, E ^ x, w ^ x)$ を次のように定義します。
$$
S _ x = S \setminus \lbrace x \rbrace, \quad
E _ x = \left \lbrace A \setminus \lbrace x \rbrace \middle \vert x \in A \in E \right \rbrace, \quad
w _ x ( y ) = w ( y ) \ ( y \in S _ x ), \\
S ^ x = S \setminus \lbrace x \rbrace, \quad
E ^ x = \left \lbrace A \middle \vert x \not \in A \in E \right \rbrace, \quad
w ^ x ( y ) = w ( y ) \ ( y \in S ^ x ).
$$
このとき、
- 一点集合 $\lbrace x \rbrace$ が $\mathcal M$ の独立集合であるとき、 $\mathcal M _ x$ はマトロイドです。
- 一点集合 $\lbrace x \rbrace$ が $\mathcal M$ の独立集合であるとき、 $\mathcal M$ の独立集合のうち、$x$ を含むものの中で重み最大であるものは、$\mathcal M _ x$ の最大重み独立集合と、$x$ の付加・除去によって 1 対 1 に対応します。
- $\mathcal M ^ x$ はマトロイドです。
- $\mathcal M$ の独立集合のうち、$x$ を含まないものの中で重み最大であるものは、$\mathcal M ^ x$ の最大重み独立集合と、ちょうど一致します。
[1 の証明] $\lbrace x \rbrace$ が $\mathcal M$ の独立集合であることから、空集合は $\mathcal M _ x$ の独立集合です。また $\mathcal M _ x$ の独立集合の部分集合もまた独立集合です。さて残るは交換性です。$A, B \in E _ x, \lvert A \rvert \lt \lvert B \rvert$ とします。このとき、$A, B$ に $x$ を付加したものを $\tilde A, \tilde B$ とおくと、これらは $\mathcal M$ の独立集合であり、$\lvert \tilde A \rvert \lt \lvert \tilde B \rvert$ が成り立ちます。したがって $\mathcal M$ の交換性より、$y \in \tilde B \setminus \tilde A$ であって、$\tilde A \cup \lbrace y \rbrace$ が $\mathcal M$ の独立集合であるものが存在します。さてこの $y$ は $B \setminus A$ にも属しており、また $x$ とは異なりますから $A \cup \lbrace y \rbrace$ は $M _ x$ の独立集合であることがわかります。以上より交換性も示され、$\mathcal M _ x$ がマトロイドであることがわかりました。
[2 の証明] まず $x$ を含む $S$ の部分集合と $x$ を含まない $S$ の部分集合が、$x$ の付加・除去によって 1 対 1 に対応していることに注意です。この対応をどんどん制限していきます。まず、$E _ x$ の定義より、この対応により片方で独立集合であることともう片方で独立集合であることが同値であることがわかります。さらに $w _ x$ の定義より、対応する $2$ つの独立集合の差は常に $w ( x )$ で定数であることがわかります。したがって、片方で最大であることともう片方で最大であることは同値です。
[3 の証明] 空集合は $\mathcal M$ の独立集合ですから、 $\mathcal M ^ x$ の独立集合でもあります。また $\mathcal M ^ x$ の独立集合の部分集合もまた独立集合です。さて残るは交換性です。$A, B \in E ^ x, \lvert A \rvert \lt \lvert B \rvert$ とします。このとき $\mathcal M$ の交換性から $y \in B \setminus A$ であって、$A \cup \lbrace y \rbrace$ が $\mathcal M$ の独立集合であるものが存在します。この $y$ は $x$ とは異なりますから、$A \cup \lbrace y \rbrace$ は $\mathcal M ^ x$ の独立集合でもあります。以上より交換性も示され、$\mathcal M ^ x$ がマトロイドであることがわかりました。
[4 の証明] 2 とほぼ同じですが、恒等対応を使います。∎
定理 4 - 3: 重み付きマトロイド上の最大重み独立集合問題における貪欲戦略の正当性
$\mathcal M = (S, E, w)$ が重み付きマトロイドであるとし、$S$ の要素を $S = \lbrace x _ 1, \dots x _ n \rbrace ( n = \lvert S \rvert)$ と、重みに関して降順になるように付番します。このとき、$S$ の部分集合 $A _ 0, \dots, A _ n$ を次のように定義します:
$$
A _ 0 = \emptyset, \quad
A _ i = \begin {cases}
A _ { i - 1 } & \left ( \mbox{ $A _ { i - 1 } \cup \lbrace x \rbrace$ が従属集合のとき} \right ) \\
A _ { i - 1 } \cup \lbrace x \rbrace & \left ( \mbox{ $A _ { i - 1 } \cup \lbrace x \rbrace$ が独立集合のとき} \right )
\end{cases}.
$$
するとこれらはすべて独立集合です。さらに、$A _ n$ は $\mathcal M$ の最大重み独立集合になっています。
[証明] $n$ に関する帰納法で証明します。$n = 0$ のときには $E = \lbrace \emptyset \rbrace$ ですから正しいです。$0 < n$ とします。
まず、一点集合 $\lbrace x \rbrace$ が従属集合であるときです。帰納法の仮定より、$A _ n$ は $\mathcal M ^ x$ の最大重み独立集合であることがわかりますから、貪欲選択性と部分問題最適性より、$A _ n$ は $\mathcal M$ の最大重み独立集合でもあることがわかります。
あとは、一点集合 $\lbrace x \rbrace$ が独立集合であるときです。再び帰納法の仮定より、$A _ n \setminus \lbrace x \rbrace$ は $\mathcal M _ x$ の最大重み独立集合であることがわかりますから、貪欲選択性と部分問題最適性より、$A _ n$ は $\mathcal M$ の最大重み独立集合であることがわかります。∎
マトロイドについてご理解、ありがとうございます!
5 - 罰金付きスケジューリング問題から作られるなにかがマトロイドになること、したがってこちらも貪欲戦略で解けること
$(n, d, w)$ が罰金付きスケジューリング問題のインスタンスであるとしましょう。すなわち $n$ がタスクの個数、$d$ が期限のリスト、$p$ が罰金のリストです。このとき、タスク番号のリストを $S = \lbrace 1, \dots, n \rbrace$、その部分集合であって適切な順番に行うとすべて期限内に実行可能であるようなもの全体の集合を $E$ とおいて、$(S, E, w)$ がマトロイドであることを証明したいです。
交換アルゴリズム
$A, B \in E, \lvert A \rvert \lt \lvert B \rvert$ としましょう。そして $A, B$ の期限に間に合う実行順を考え、$A, B$ に含まれる要素全体をそれぞれ実行順に $a _ 1, \dots, a _ k, b _ 1, \dots b _ l \ ( k \lt l )$ とおいておき、$A, B$ を集合ではなく列とみなしましょう。
このような列 $A, B$ を入力して、列 $C$ であって次の条件
- $C$ は $k + 1$ 元集合で、
- $C$ に含まれる要素のうち $k$ 個は $A$ に、残りの $1$ 個は $B \setminus A$ に属しており、
- $C$ を並び順に実行するとすべて期限に間に合います。
を満たすものを $A$ に代入するアルゴリズムをご紹介しましょう。
交換アルゴリズムの定義
こうです。動きが分かりづらく、停止性も明らかではないため狐につままれがちですが、実はこれで動きます。
- $i = k + 1$
- $a$ に $b _ { k + 1 }$ を push します。
- while $i \neq j, b _ i = a _ j$ なる $j$ が存在する
- $a _ j \leftarrow b _ j$
- $i \leftarrow j$
- $a _ j \leftarrow b _ j$
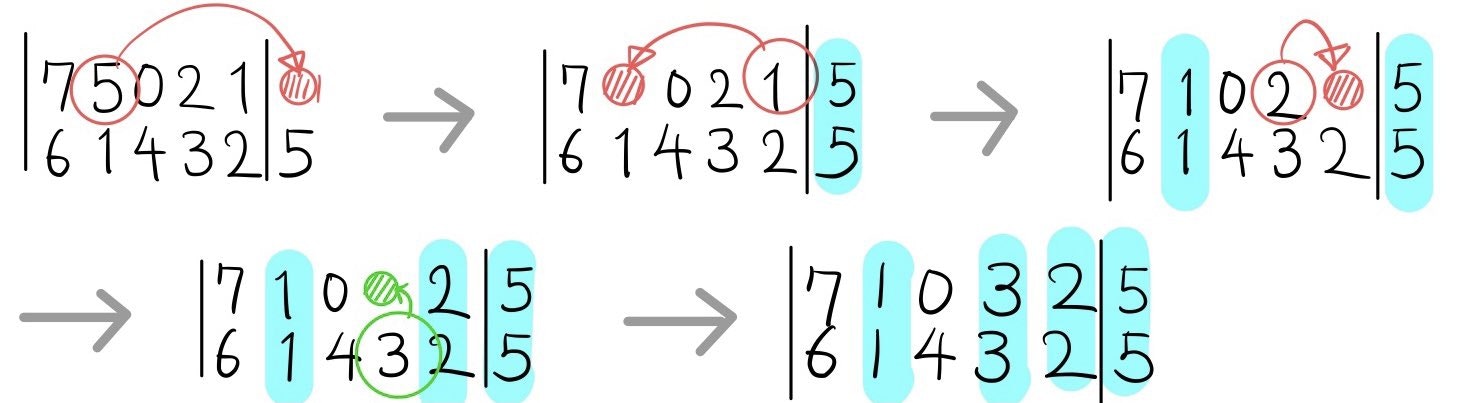
イメージはこちらです。しばらく前に書いてしまった都合上 $0$ が入っており一貫性がないですし、上の疑似コードでは $a$ の要素に常に重複があるようにしている一方図ではその代わりに穴が $1$ つ空いている形になっています。やや対応していなくてもうしわけないのですが、このようにします。
上側が $A$, 下側が $B$ であり、書いてあるのはタスク番号と思っていただけると嬉しいです。$A$ の $k + 1$ 個目ははじめ空欄になっており、アルゴリズム中もどこかしら一箇所が空欄である感じで進めていきます。
$i$ 番目が空欄のであるとき、$B _ i$ をそこに埋めます。そしてそれでダブリが出てしまったら、もともとあったほうを消します。このアルゴリズムにおいては若者が優先です。
これを繰り返すと実はいつか停止し、さらにもとの $A$ に $B \setminus A$ の要素がひとつ付け加えられた形になり、さらにすべて期限に間に合うことが証明できます。それはこれからやっていきましょう!
交換アルゴリズムの正当性・停止性
while ループの条件チェック直前において、次のことが成り立っていることを証明します。
- $a _ i = b _ i$
- $A$ はこの順に行うとすべて期限内に終わります。(同じタスクが $2$ つ入っている場合は $2$ 回行って、両方共期限内とします。)
- $A$ から $i$ 番目を覗いたものには重複がありません。
周回数に関する帰納法で証明します。まず一周目は $i = k + 1$ は新しく挿入した要素ですが、もともと $B _ i$ だったものですから期限に間に合うことが保証されています。残りの $k$ 個の要素は実行可能解を為しますから、当然 distinct ですし、期限にも間に合います。
ある周回で while ループの継続条件が true であったとすると、条件チェック直後時点で $a$ のタスクはすべて時間に間にあい、$(i, j)$ が $a$ の唯一の重複ですから、$a$ は $j$ 番目を除いて distinct です。そのあと $a _ j$ が変更になるのですが、これで条件は壊れません。さらにこの $j$ が $i$ に代入されますから、結局 $A$ は $i$ 番目を除いて distinct になります。
あとは停止性です。$a _ i = b _ i$ を満たす $i \in \lbrace 1, \dots, k \rbrace$ の個数 $Q$ に着目します。この量が変動する可能性のある箇所は疑似コード中の $a _ j \leftarrow b _ j$ とある箇所のみです。
ここできっかり $1$ 増加すること、すなわち代入前には $a _ j \neq b _ j$ であったことが示しましょう。まず先程示した命題より $a _ i = b _ i$ であり、また while ループの継続条件より $a _ i = a _ j, i \neq j$ です。さらに $B$ が distinct であったことから $b _ i \neq b _ j$ ですから、以上まとめて、$a _ j \neq b _ j$ が従います。
よってループ一周ごとにこの量 $Q$ は $1$ 増加し、またこれは $0$ から $k$ の間ですから、たかだか $k$ 回しか回りません。したがってこのアルゴリズムは停止し、実行時間は $O ( k )$ です。(ちなみに最悪ケースも作れて、$A _ i = B _ { i + 1 }$ になるようにするとよいです。)∎
以上より、罰金付きスケジューリング問題の実行可能タスク集合全体の集合がマトロイドをなすことがわかり、重み付きマトロイド上の最大重み独立集合のアルゴリズムが使えることがわかりました。すなわちタスクを罰金の降順に見ていき、追加できるならばする、できないならばスキップを繰り返せば良いことがわかりました。
6 - ところで間に合うかどうかってどのように判定するのですか?
解けた気になっていますでしょうか。まだですよ!(脱出しようとする皆様の脚を引っ掛けるポーズ)実装してみようと思うと気づくと思うのですが、「このタスクを入れても実行可能であるか」の判定ができなければこまってしまいますね。
実は、うまく並び替えると間に合うようなタスクセットは、期限の降順に実行してもすべて間に合うことが証明できます。生活に役立つ知見ですね。こちらも一種の貪欲戦略なのですが、空間が置換全体の数合であり、冪集合の形をしていないことなどを考えると、マトロイドで考えるのは少しむずかしそうです。
ではどうするかというと、これも貪欲戦略の正当性証明の典型テクニックなのですが、「最適解を変形して貪欲戦略にする」という手法を使います。特に今回のように置換からなる集合の上で最適化問題をするときには、「隣接スワップで貪欲戦略に近づける」が非常に有効です。
期限の降順戦略の正当性
$A \in E$ として、タスク $i, j$ の実行時刻が $a _ i \gt a _ j$、期限が $d _ i \lt d _ j$ だとします。このとき $i, j$ の実行時刻を入れ替えても期限を過ぎないことを証明します。
まず、$A \in E$ よりもともと期限は過ぎておらずでしたから、$a _ i \le d _ i, a _ j \le d _ j$ が成り立ちます。更に $i, j$ に関する仮定より、$a _ i \le d _ i \lt d _ j, a _ j \lt a _ i \le d _ i$ が成り立ち、入れ替えても間に合うことがわかりました。
と言うわけで、この要領でソートしていくことで、貪欲戦略にすることができます。厳密にやりたい場合は、$a$ と $d$ の間の転倒数
$$
\left \lbrace (i, j) \middle \vert a _ i \lt a _ j, d _ i \gt d _ j \right \rbrace
$$
に関する帰納法を用いると良いです。∎
7 - 互いに素な集合の森(union-find)を用いて罰金付きスケジューリング問題(ソート済み)を Θ(nα(n)) で解きます。
今までのお話をまとめると、大まかにはこのようなことをするとよいです。$(n, d, p)$ が罰金付きスケジューリング問題のインスタンスであり、罰金 $p$ が降順であると仮定しましょう。そのような $(n, d, p)$ を受け取って、行うべきタスクとその実行順 $a$ を返すアルゴリズムを設計します。
- $a$ を空配列とします。
- for $i \in \lbrace 1, \dots, n \rbrace$
- if $a$ に $i$ を加えたものは実行可能であるならば、
- $a$ に $i$ を加えます。
- if $a$ に $i$ を加えたものは実行可能であるならば、
「$a$ に $i$ を加えたものは実行可能である」というのを速く判定する方法を考えていきましょう。
ナイーブな解法
タスクを採用するたびに可能な限り遅い時刻を割り振って、「どの時刻が埋まっているか」を管理しましょう(これで大丈夫なこと、証明するのがつかれたので省略でよろしいでしょうか……)。するとこのようになります。
- $a$ を空配列とします。
- $c$ が長さ $n$ の boolean 配列で、false で初期化されているとします。
- for $i \in \lbrace 1, \dots, n \rbrace$
- if $c _ j = \mathtt { false }, j \le d _ i$ なる $j$ が存在するならば、
- $c _ j = \mathtt { true }$
- $a$ に $i$ を加えます。
- if $c _ j = \mathtt { false }, j \le d _ i$ なる $j$ が存在するならば、
「存在するならば」というところは、線形探索をしていきましょう。これで曖昧さはなくなったでしょうか。このアルゴリズムは $O ( n ^ 2 )$ で動きます。最悪ケースは作れますから $\Theta ( n ^ 2 )$ ですね。
チョーカッチョイイ解法
互いに素な集合の森(素集合データ構造 - Wikipedia, union-find)と呼ばれるデータ構造があります。
このデータ構造は互いに素な集合の族(言い換えるとある集合の非空な集合への分割) $\mathcal A$ を管理し、次の操作ができます。(詳しくご説明する体力は残っておらずです!)
| 操作 | 効果 | 計算量 | 制約 |
|---|---|---|---|
| $\mathtt { new } ()$ | 空集合を構築します。 | $\Theta ( 1 ) $ | |
| $\mathtt { add } (x)$ | 一点集合 $\lbrace x \rbrace$ を $\mathcal A$ に追加します。 | $\Theta ( 1 ) $ | $x \not \in \bigcup \mathcal A$ |
| $\mathtt { find } (x)$ | $x \in A \in \mathcal A$ なる $\mathcal A$ を返します。 | $\Theta ( \alpha ( n ) ) $ | $x \in \bigcup \mathcal A$ |
| $\mathtt { unite } (x, y)$ | $\mathtt { find } (x)$ と $\mathtt { find } (y)$ を $\mathcal A$ から取り除き、両者の合併を追加します。 | $\Theta ( \alpha ( n ) )$ | $x, y \in \bigcup \mathcal A$ |
(ただし $n$ は要素数 $\left \lvert \bigcup \mathcal A \right \rvert$ です。$\alpha$ は「アッカーマン関数の逆関数」と呼ばれる、非常にゆっくり増加する関数です。そろそろ記事を閉じたいのでご勘弁いただけないかと……)
チェックリストを直接管理するのをやめて、このデータ構造を使って、チョーカッチョヨク管理していこうと思います。
チェックリストと互いに素な集合の対応
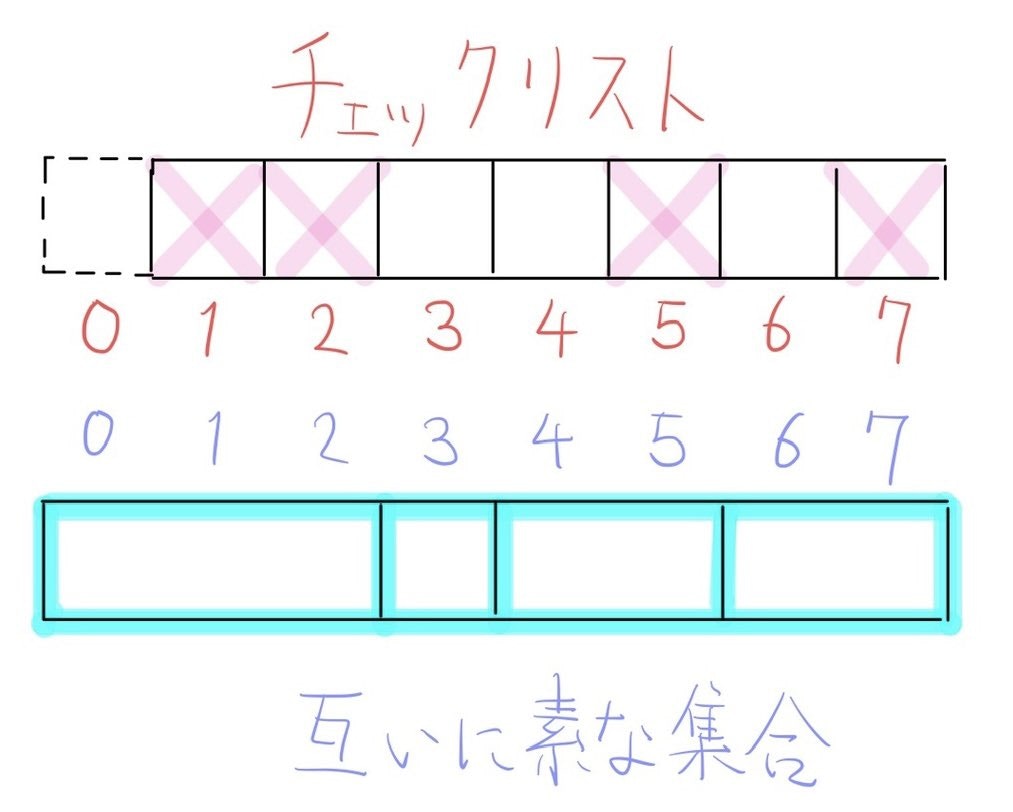
まずチェックリストの $1$ 番目のの左に番兵さんをいれて、$0$ と名付けましょう。ここは常に false が入っているものとしましょう。それに対して、「各 false の左で切る」方式で、区間 $\lbrace 0, \dots, n \rbrace$ の非空な区間への分割に対応しましょう。逆にそのような区間分割が与えられたら「各成分の左端以外をすべて true を埋める」方式で対応しましょう。これによりちょうど一対一対応します。
絵を描きましょう。かわいらしいと思います。
互いに素な集合で必要な操作を実現する方法
今回のアルゴリズムで必要な操作は $2$ つです。
- ある場所かそれより左にある false を発見する
- ある場所のチェックを true に変更する
1 のほうが楽です。$\mathtt { find }$ を呼んで自分の属する連結成分を返すと良いです。ただしそれがもっとも左の連結成分であるときには、$0$ に対応する false を指すことににあり、これは結局 $\lbrace 1, \dots, n \rbrace$ の中では目的の false が探せなかったことになります。
2 は、一つ右の連結成分と $\mathtt { unite }$ すると良いです。
また、今回はそこまで入りませんが、本当に添字自体がほしいときには連結成分に「左端の添字」をもたせておくと良いです。
「一つ左」はどうやって取るのですか?
片方向連結リストに入れましょう!(もう投げやりになってすみません……)
疑似コード
- 互いに素な集合の森であって、$\lbrace \lbrace 1 \rbrace, \dots, \lbrace n \rbrace \rbrace$ に対応するものを構築して、$T$ とおきます。
- $T$ に属する集合全体を要素全体とし、各々中身の数が $1$ 小さいものを後者とするような単方向連結リスト $L$ を構築します。
- $L$ に入れたノードのハンドラを中身の数に関して降順に、すべて配列にいれて $H$ と置きます。
- 空配列 $a$ を構築します。
- for $i \in \lbrace 1, \dots, n \rbrace$
- $h = \mathtt { find } \left ( T, H _ { d _ i } \right )$
- if $h$ が $L$ の先頭ノードでない
- $h$ とその次のノードを $T$ においても $L$ においてもつなげます。
- $a$ に $i$ 挿入します。
- if $h$ が $L$ の先頭ノードでない
- $h = \mathtt { find } \left ( T, H _ { d _ i } \right )$
というわけで、互いに素な集合の森と単方向連結リストを使うと高速に解くことができることがわかりました。マトロイドからはずいぶんと話題がずれてしまいましたね。
8 - 宣伝
キャディという会社があってですね、詳しくはこちら のエンジニア採用サイトをご覧いただきたいのです。難しい課題がたくさんあり、皆さん真剣に取り組んでいるとても面白いところです。皆様もぜひです!
9 - 追記 2020-02-21
AtCoder のこちら、初手の考察以外を抜けるとあとは罰金付きスケジューリング問題やるだけなので練習にどうぞです。