こんにちは、ながたかなです。
今回は平衡二分木の実装において軽視されがちな「どこで update, push するか問題」について真剣に考察してみました。ぜひともみなさまのご指摘・ご意見・チャンネル登録・高評価・ツイッターインスタグラムのフォロー・焼き肉などをいただきたいです。
1 二分木の頂点重みの集約、二分木の頂点重みへの作用
このあたりのお話はセグメント木の遅延伝播と同じですからおなじみかとは思うのですが、記号や用語の導入を兼ねて一応です。
二分木の(内部節点を含む)すべての節点になんらかの重み $v \mapsto v.\mathrm { value }$ (今後、$v$ と $v . \mathrm { value }$ のを混同して書くことがあります。)が定義されており、頂点の値の間の結合的な二項演算 $( x, y ) \mapsto x \cdot y = x y$ 、それと整合的(i.e. $f ( x y ) = f ( x ) f ( y )$ )な頂点の値への作用 $x \mapsto f ( x )$ が定義されているとします。このとき、次のことを $O ( \mathrm { height } )$ でしたいです。(とは言っても実際に計算するアルゴリズムについてはこの記事ではお話しません。併用する平衡アルゴリズムによっても事情の異なることですし。)
- ある区間のすべての頂点についての値を順番に、演算 $(x, y) \mapsto x \cdot y$ で集約した値を知りたいです。
- ある区間のすべての頂点について、値を $v . \mathrm { value } \mapsto f ( v . \mathrm { value } )$ と更新したいです。
1.1 集約
詳細はともかく、概ねつぎのことをすると思います。まず集約だけの場合はこちらです。
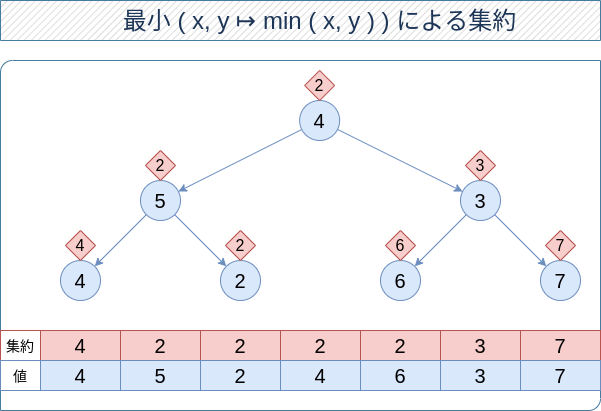
- 各頂点 $v$ について、集約値 $v . \mathrm { acc }$ を管理します。これは $v$ の部分木について集約した値になるように保ちます。
たとえばこちらのようになります。赤い菱形が部分木の値を最小演算で集約した結果です。
1.2 作用
作用がある場合は、それを遅延伝播方式でおこないます。すなわち、ある瞬間の $v . \mathrm { value }, v . \mathrm { acc }$ は真の値、真の集約値とは異なる場合がある、というのを許容しましょう。
- 各頂点 $v$ について、作用値 $v . \mathrm { lazy }$ を管理します。不変条件は「$v . \mathrm { value }$ に $v$ の祖先全ての $\mathrm { lazy }$ を順番に施したとき、$v$ の真の値に一致するようになっている」ことです。
- また $v . \mathrm { acc }$ についての不変条件は「$v . \mathrm { acc }$ に $v$ の祖先全ての $\mathrm { lazy }$ を順番に施したとき、$v$ の部分木の真の集約値に一致するようになっている」です。
以後単に「不変条件」といえばこの2条件がともに成り立つことを指すとしましょう。
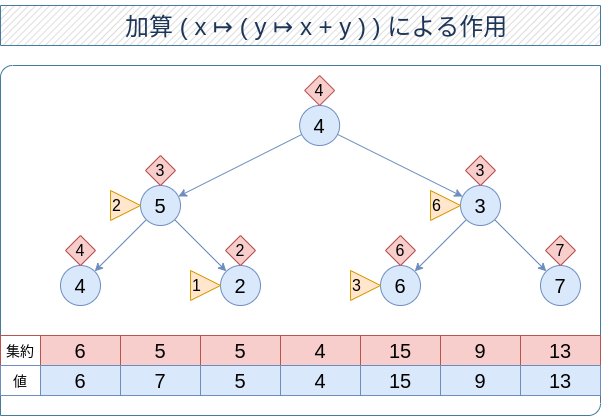
たとえばこちらのようになります。黄色い三角が部分木への加算作用です。実際になんらかのアルゴリズムでこれが生じることがあるかどうかはともかく、不変条件は満たしているのではないかと思う、今日このごろです。
なお二分木では部分木サイズ、リバースフラグ(ある区間の頂点の並び順を逆順にするフラグ)を管理する場合がありますが、いつ更新するかという観点では、前者は $\mathrm { acc }$、後者は$\mathrm { lazy }$ と同じですからこの記事では言及しないことにします。(ちなみにリバースフラグをつけると演算に関する要請が強まるので注意です。)
1.3 集約値の更新 (update)
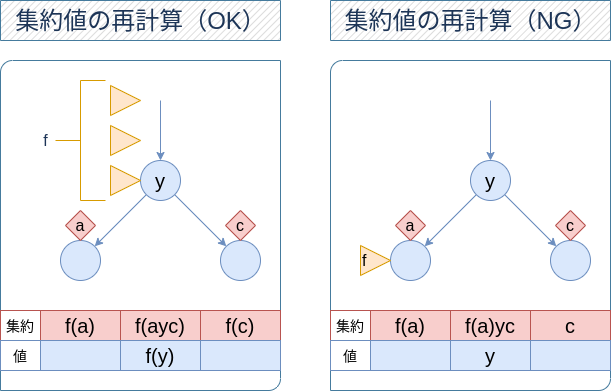
アルゴリズム進行上のなんらかの理由である頂点の集約値が不変条件を満たさなくなったとき、それを再計算することを、この記事では update と呼ぶことにします。このとき「単純に再計算するだけ」($v . \mathrm { acc }$ に $v . \mathrm { left } . \mathrm { acc } \cdot v . \mathrm { value } \cdot v . \mathrm { right } . \mathrm { acc }$ を代入する)で修正できるための事前条件を考えましょう。
まず作用がない場合は左右の部分木の集約値が正しければそれでよいです。作用がある場合は非自明なのですが、この場合は実はそれに加えて
- 両方の子の $\mathrm { lazy }$ が恒等作用
が成り立つ必要があります。逆にこれさえ成り立っていれば、自分やその祖先にどれだけ作用が残っていても構いません。一方どちらかの子に恒等的でない作用が残っている場合は、「単純に再計算するだけ」ではだめです。
というわけで「update の前にはとにかく脳死で子を push」という戦略が思いつくわけなのですが、ここで不安になるわけです。「えっこの push って呼んでいいんですかね。push の事前条件を満たすために念の為周辺の頂点に一通り update を呼んで、アッでもこの update の事前条件のアでも push アでもアァァアアアブォオオオン(爆発オチ)」とならないでしょうか。それについては次節です。
1.4 作用の伝播 (push)
作用の伝播は、不変条件を回復する集約値の更新とは異なり、もともと不変条件を満たしていた木の特定の頂点の作用値を、不変条件を保ったまま恒等作用にするための操作です。これは push, eval, propagate などと呼ばれますが、この記事では push と呼ぶことにします。
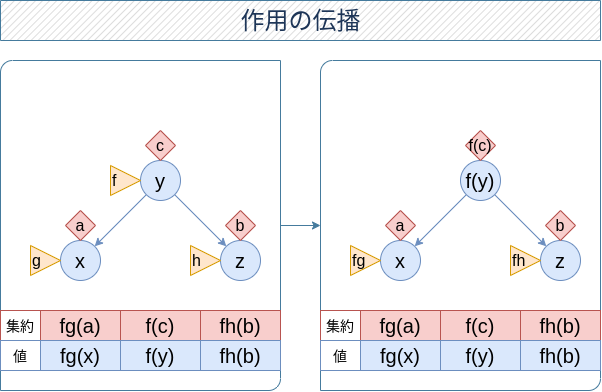
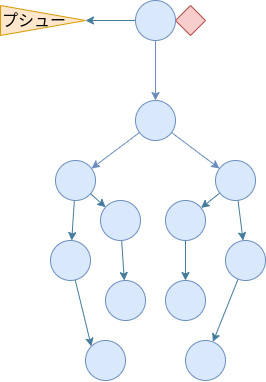
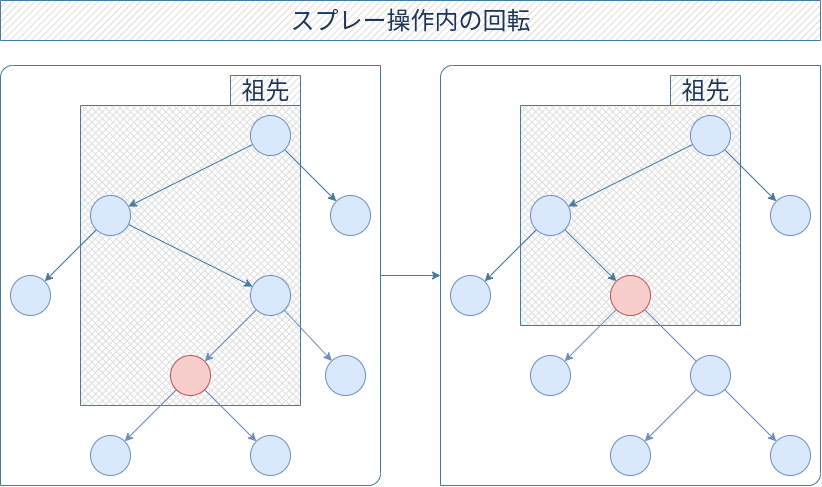
さて push の事前条件について考えたいのですが、実はこれは操作頂点とその部分木の頂点が全て不変条件を満たしていればよいです。このことは次の図からわかるわけですね。(真祖先頂点の作用値は、単純化のために省略しています。)
というわけで、update したい状況(ある頂点の $\mathrm { acc }$ が不変条件を満たさず、その真部分木は不変条件を満たすとき)には子の push を呼んで大丈夫なことがわかりましたね。めでたしめでたし。これで遅延伝播機能付き平衡機能なし二分木が作れるわけです。(それほぼただの遅延セグ木では)
1.5 アルゴリズム進行上、update, push の必要なケース
そもそもなにもしなければ壊れないわけです。いつ治す必要があるのかをお話します。平衡アルゴリズムによってはそもそもやらなくて済む操作もありますが、任意の構造のまま諸操作をしないと行けない状況と思ってお話します。(特に、スプレー木はやや事情が異なる部分があります。)また煩雑なので、この節では update 前の2回の push への言及は省略することにします。
- 構造変更(回転) → 難しいのであとでお話します。
- 頂点の値の取得 → その頂点の祖先に上から順に push を呼びましょう。
- 頂点の値の更新 → その頂点の祖先に上から順に push を呼び、操作後にその頂点の祖先に下から順に update (と付属の push )を呼びましょう。
- 部分木の集約値の取得 → その頂点の祖先に上から順に push を呼びましょう。
- 部分木への作用 → その頂点の祖先に上から順に push を呼び、操作後にその頂点の祖先に下から順に update (と付属の push )を呼びましょう。
- 辺の削除 → 操作前に親側の頂点の祖先に上から順に push を呼び、操作後に親側の頂点の祖先に下から順に update (と付属の push )を呼びましょう。
- 辺の追加 → 操作前に親側の頂点の祖先に上から順に push を呼び、操作後に親側の頂点の祖先に下から順に update (と付属の push )を呼びましょう。
結局何をするにしても、上から push、頂点重みか作用値が変わる場合は加えて下から update という感じになるわけです。
さらになにかしたあとに回転しながらボトムアップしていくタイプの平衡アルゴリズム(赤黒木など)を併用している場合は、この update と回転によって必要になる update, push を適宜両方捌かないと行けずちょっと大変なわけですが、最悪ボトムアップフェーズを2回やって1周目で下から update、2周めで構造変更 + それに伴う update, push とすればできなくはないわけです。(おそらく効率は悪いですが。)
2 回転
多くの平衡アルゴリズムは、適宜二分木の回転を呼ぶことで構造を変更して平衡を保つわけですが、このときどうしたら不変条件を壊さないのか。またどうしたら update, push の回数をできるだけ少なくできるかが気になるお年ごろなわけです。
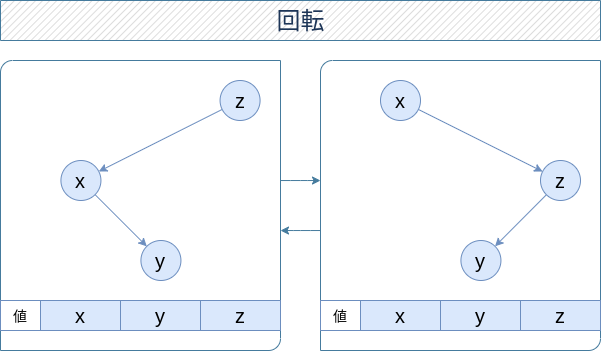
回転というのは、図のように親子関係にある 2 つの頂点の深さを入れ替え、同時に子を片方押し付け合う操作なわけです。今後特に断りがなければ、図の左の構造から右の構造に変える操作を考えるとします。
実際にどのようにポインタを張り替えると良いのかは、こちらの動画(回転の説明の始まる 9:13 に合わせてあります。)がとてもわかりやすいです。
2.1 集約値
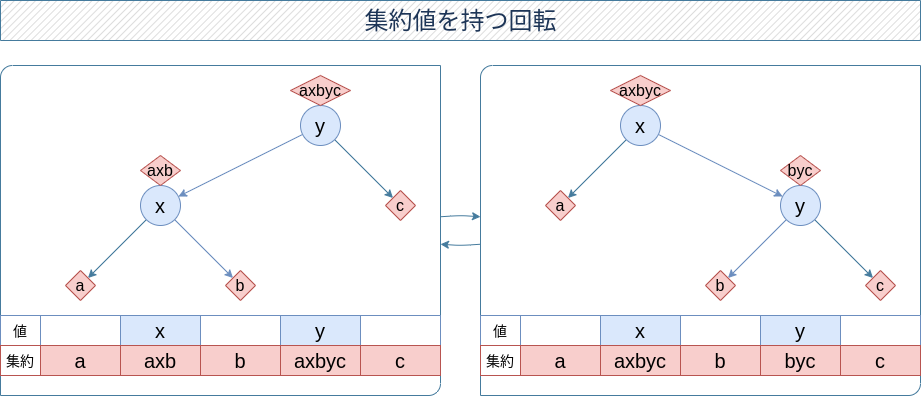
集約値は図のような結果を目指しましょう。そのためには上の動画のようにポインタを張り替えたあと、
- $y$ を $\mathrm { update }$
- $x$ を $\mathrm { update }$
をするとよいです。
いえいえしかし我々は「集約値更新、作用の伝播呼び出し回数絶対下げるマン」なわけです。左右どちらの図でも一番上の頂点の集約値が $axbyc$ で等しいことに着目しましょう。そこで
- $x$ の集約値に $y$ の集約値を代入(またはスワップ)
- $y$ を update
という方法が取れることに気づくわけですね。これで update の回数が2回から1回に減らすことができました。(なお集約演算が十分に速い場合はパフォーマンスはほぼ変わらないと思います。気持ちの問題ですね〜〜真心♡コーディングです。)
2.2 作用
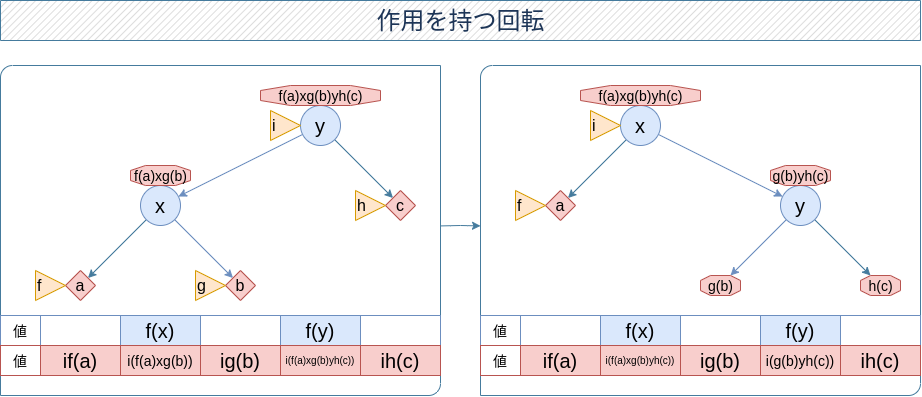
作用もある場合を考えましょう。ここいきなり考えると混乱しがちで、「とにかく関係ありそうな頂点を上から順に push していけばなんとかなるやろエーーーい 」になりがちです。しかし今までのお話を総動員していくと自然にアルゴリズムが降ってくるわけです。アーメンつけ麺僕イケメンです。
- $x$ を push (図ではすでにやった感じにして省略してあります。)
- ポインタの張替え
- $y$ の集約値、作用値を $x$ にコピー
- $y$ の両方の子を push
- $y$ を update
というわけで、update 1回、push3回でできるわけです。 また update サブルーチンの中に push 2回を入れている場合、その push も無駄にならない(今回呼びたいものの一部になっている)わけです。
3 スプレー木のスプレー
スプレー木の update, push タイミングは(先述の汎用的なものを使うこともできますが)少し特殊な戦略を取ることが多いです。
スプレー木といえばスプレーです。スプレーは操作頂点のもともとの深さ $d$ と等しい回数の回転の繰り返しです。スプレーが終わるまでは特に値にアクセスするわけではありませんから、トップダウンフェーズに push する必要はありません。する戦略もしない戦略もあります。諸々のやり方を比較検討していきましょう。
3.1 回転におまかせ
もともと全ての頂点について不変条件が成り立っているならば、1回の update と3回の push を併用することで、どんなに唐突な場所の回転でも必ず不変条件を保存できるマスター戦略がありましたね。それを使うと update $d$ 回、push $3 d$ 回です。
3.2 すべてトップダウンフェーズに push
左右の子を push するのを祖先全体について上から順に行います。これをしておくと実はボトムアップフェーズの push は一切不要になり、update $d$ 回、push $2 d$ 回を達成します。
それを証明していきましょう。まず初回の回転は例えば自分を回転する場合は関連頂点が(親が根だった場合、親以外)すべて $\mathrm { lazy }$ が恒等作用になっているので明らかに大丈夫ですね。また親を回転する場合も同様に大丈夫です。またスプレー操作内の回転はこの「操作頂点の各祖先の両方の子の $\mathrm { lazy }$ は恒等作用」という条件を保存しますから、2回目以降もよいです。
この戦略の嬉しいところは、単に push の呼び出し回数が少ないということだけでなく、トップダウンフェーズに push して $\mathrm { lazy }$ を恒等作用にした $2 d$ 子の頂点の $\mathrm { lazy }$ が全て、スプレー終了後にも恒等作用になっていることです。厳密な評価でなくて申し訳ないのですが、基本的に $\mathrm { lazy }$ が恒等作用である頂点が多ければ多いほど、push 内部の場合分けでスキップされる可能性が高くなって早くなりがちという直感があります。
3.3 すべてトップダウンフェーズに push するし、帰りにもなぜか push する
3.2、3.1 の両方を行うということです。update $d$ 回、push $4 d$ 回になるわけですが、帰りの push $2 d$ 回はすべて恒等作用になっていのでそこを場合分けでスキップしている場合は実質 $2 d$ 回です。
3.4 すべてボトムアップフェーズに push するけど回転におまかせしない
これが一番普及しているのではないかと思っています。他に比べて遜色ないとはいえ実装の単純さ・定数倍どちらにおいても圧倒的な優位性があるとまではいえなさそう(つまりニュートラル)ですし、偏るのが不思議です。
具体的には、
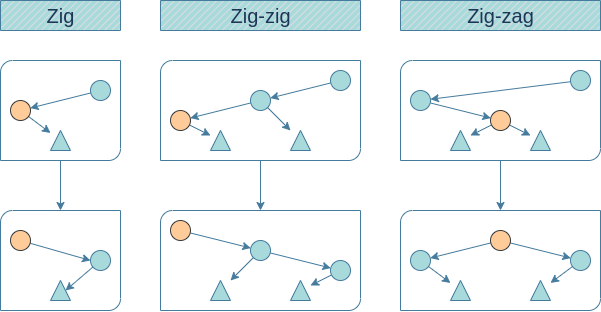
- zig case ならば 親と自分を順に push
- zig-zig case, zig-zag case ならば親の親と親と自分を順に push
- 回転したら2回 update
- update 内で push 2回呼び出し
という戦略です。有名所でいうと、(LC 木ですが)Link-Cut木(Link-Cut-Tree) | Luzhiled’s memo もこの戦略です。この戦略は update $2d$ 回、push $5 d$ から $6 d$ 回です。さらに回転で $\mathrm { acc }$ と $\mathrm { lazy }$ のコピーを使って update を1回にするテク(これなしで比較するのはちょっと不公平な感じがするので入れておきます。)を使うと update $d$ 回、push $3 d$ から $4 d$ 回以下です。操作後に $\mathrm { lazy }$ が残ってしまうというデメリットはあるものの、操作回数自体は遜色なしくらいです。
3.5 結局どれを使えばよいですか?
AOJ のコースで何通りか提出して比較してみたところ高々 1.5 倍程度でしたからこの中の戦略なら割とどれでも大丈夫だと思います。「これで正しい」という確信を持って書けるのが最重要です。他の平衡アルゴリズムでも使える汎用的な回転が案外そこそこ効率が良いですから、個人的にはそれが入門フレンドリかなと感じております。
ちなみになのですが、AOJ のコースはクエリがかなり軽い問題しかないですから、重いものだとひょっとすると差がでるかもしれませんね。(なかなかそこが重い問題って見かけませんが。