【Machine Learning】Vietnamese - Automated Hyperparameter Tuning (Updating)

1. Mở đầu.

Bài viết gốc tại đây: Introduction: Automated Hyperparameter Tuning

Trong bài viết này, chúng ta sẽ nói qua một ví dụ hoàn chỉnh về việc điều chỉnh Hyperparameter (siêu tham số) một cách tự động để tối ưu hóa các mô hình học máy. Cụ thể, chúng ta sẽ sử dụng Bayesian Optimization và thư viện Hyperopt để điều chỉnh Hyperparameter của mô hình máy học tăng cường độ dốc(gradient boosting machine).

Có 4 cách tiếp cận để điều chỉnh Hyperparameter của mô hình học máy:
1. Cách thủ công: Chọn các Hyperparameter dựa trên trực giác / kinh nghiệm / đoán, huấn luyện mô hình với Hyperparameter và đánh giá trên dữ liệu validation. Lặp lại quá trình cho đến khi bạn hết kiên nhẫn hoặc hài lòng với kết quả.
2. Grid Search(Tìm kiếm lưới): Thiết lập một "lưới" các giá trị Hyperparameter, và với mỗi bộ tham số được kết hợp ta huấn luyện một mô hình, sau đó đánh trên bộ dữ liệu validation. Trong phương pháp này, tất cả sự kết hợp đơn lẻ của các bộ Hyperparameter đều được thử, do đó có thể rất kém hiệu quả, tốn tài nguyên tính toán!
3. Random search (Tìm kiếm ngẫu nhiên): thiết lập một "lưới" các bộ giá trị Hyperparameter và chọn các kết hợp ngẫu nhiên để huấn luyện mô hình và đánh giá trên tập dữ liệu validation. Số lần lặp tìm kiếm được thiết lập dựa trên thời gian / tài nguyên.
4. Automated Hyperparameter Tuning(Điều chỉnh siêu tham số tự động): sử dụng các phương pháp như giảm độ dốc, tối ưu hóa Bayes hoặc thuật toán tiến hóa để tiến hành tìm kiếm Hyperparameters tốt nhất.

Ở đây chúng ta sẽ chỉ tập trung vào tối ưu hóa Bayes (Bayesian Optimization), sử dụng Esimator Tree Parzen (đừng lo lắng, bạn không cần phải hiểu chi tiết điều này) trong thư viện mã nguồn mở Hyperopt của Python.

Để có thêm một chút nền tảng (chúng tôi sẽ đề cập đến mọi thứ bạn cần bên dưới), đây là một bài viết giới thiệu về tối ưu hóa Bayes link, và đây là một bài viết về điều chỉnh siêu tham số tự động bằng cách sử dụng tối ưu hóa Bayes Link. Ở đây chúng ta sẽ đi thẳng vào điều chỉnh siêu tham số tự động, vì vậy để có nền tảng cần thiết về điều chỉnh siêu tham số cho mô hình máy học, hãy tham khảo kernel này.

2. Tối ưu hóa Bayes (Bayesian Optimization)

Vấn đề với grid search và random search là chúng là các phương pháp không được xác định (uninformed methods) bởi vì chúng không sử dụng các kết quả trong quá khứ từ các giá trị khác nhau của hyperparameters trong hàm mục tiêu (hãy nhớ hàm mục tiêu sử dụng các hyperparameters và trả về the model cross validation score).

Chúng ta ghi lại kết quả của hàm mục tiêu cho từng bộ hyperparameter, nhưng các thuật toán này không chọn các giá trị hyperparameter tiếp theo dựa theo thông tin này.

Theo trực giác, nếu chúng ta có kết quả trong quá khứ, chúng ta nên sử dụng chúng để suy luận về giá trị hyperparameter nào hoạt động tốt nhất và chọn các giá trị tiếp theo một cách khôn ngoan để thử và dành nhiều lần lặp hơn để đánh giá các giá trị hứa hẹn.

Việc đánh giá các hyperparameter trong hàm mục tiêu rất tốn thời gian và khái niệm tối ưu hóa Bayes là để giới hạn việc gọi đến hàm đánh giá bằng cách chọn các giá trị hyperparameter tiếp theo dựa trên các kết quả trước đó. Điều này cho phép thuật toán dành nhiều thời gian hơn để đánh giá các giá trị hyperparameter hứa hẹn và tốn ít thời gian hơn trong các khu vực có điểm số thấp của không gian hyperparameter.
Ví dụ, hãy xem xét hình ảnh dưới đây:

Nếu bạn đang chọn số lượng cây tiếp theo để thử cho khu rừng ngẫu nhiên, bạn sẽ tập trung tìm kiếm ở đâu? Có lẽ khoảng 100 cây vì đó là nơi xảy ra lỗi thấp nhất (hãy tưởng tượng đây là vấn đề chúng ta muốn giảm thiểu lỗi).

Trong thực tế, bạn vừa thực hiện tối ưu hóa siêu tham số Bayes trong đầu của bạn! Bạn đã hình thành một mô hình xác suất của lỗi là một hàm của hyperparameter và sau đó chọn các giá trị hyperparameter tiếp theo bằng cách tối đa hóa xác suất xảy ra lỗi thấp(the probability of a low error).

Tối ưu hóa Bayes hoạt động bằng cách xây dựng hàm thay thế/đại diện (dưới dạng mô hình xác suất) của hàm mục tiêu P(score|hyperparameters. Phỏng đoán một hàm thay thế rẻ hơn nhiều so với mục tiêu, vì vậy thuật toán này chọn các giá trị tiếp theo để thử hàm mục tiêu dựa trên việc tối đa hóa một tiêu chuẩn của hàm thay thế (thường là sự cải thiện kỳ vọng), chính xác như những gì bạn sẽ làm đối với hình ảnh ở trên.

Hàm thay thế dựa trên các kết quả đánh giá trong quá khứ - các cặp bản ghi (score, hyperparameter) - và được cập nhật liên tục với mỗi đánh giá hàm mục tiêu.

Tối ưu hóa Bayes vì thế sử dụng lý luận Bayes: tạo thành một mô hình ban đầu (được gọi là trước) và sau đó cập nhật nó với nhiều bằng chứng hơn. Tạo thành một mô hình ban đầu (được gọi là prior) và sau đó cập nhật nó với nhiều bằng chứng hơn.

Ý tưởng là khi dữ liệu được tích lũy, hàm thay thế càng ngày càng gần với hàm mục tiêu và các giá trị hyperparameters tốt nhất trong hàm thay thế cũng sẽ làm tốt nhất trong hàm mục tiêu.

Các phương pháp tối ưu hóa Bayes khác nhau trong thuật toán được sử dụng để xây dựng hàm thay thế và chọn các giá trị siêu tham số tiếp theo để thử.

Một số lựa chọn phổ biến là Quy trình Gaussian (được implemented trong Spearmint), Hồi quy rừng ngẫu nhiên (trong SMAC) và Công cụ ước tính cây (TPE) trong Hyperopt (có thể tìm thấy chi tiết kỹ thuật trong bài viết này, mặc dù chúng không cần thiết sử dụng các phương pháp).

2.1. 4 phần của tối ưu hóa Bayes

Tối ưu hóa siêu tham số Bayes yêu cầu 4 phần giống như chúng ta đã thực hiện trong tìm kiếm ngẫu nhiên và grid search:
1. Hàm mục tiêu(Objective Function): lấy một đầu vào (hyperparameter) và trả về điểm số để giảm thiểu hoặc tối đa hóa (the cross validation score)

2. Không gian tên miền: phạm vi của các giá trị đầu vào (hyperparameters) để đánh giá

3. Thuật toán tối ưu hóa: phương pháp được sử dụng để xây dựng hàm thay thế và chọn các giá trị tiếp theo để đánh giá

4. Kết quả: score, cặp giá trị mà thuật toán sử dụng để xây dựng hàm thay thế
Sự khác biệt duy nhất là bây giờ hàm mục tiêu của chúng ta sẽ trả về score để giảm thiểu (đây chỉ là quy ước trong lĩnh vực tối ưu hóa), không gian miền của chúng tôi sẽ là phân phối xác suất thay vì "lưới" hyperparameters,
và thuật toán tối ưu hóa sẽ là một phương pháp informed sử dụng các kết quả trong quá khứ để chọn các giá trị hyperparameters tiếp theo để đánh giá.

2.2. Hyperopt

Hyperopt là một thư viện Python mã nguồn mở, thực hiện Tối ưu hóa Bayes bằng thuật toán Ước tính Tree Parzen để xây dựng hàm thay thế và chọn các giá trị hyperparameters tiếp theo để đánh giá trong hàm mục tiêu.
Có một số thư viện khác như Spearmint (hàm thay thế quy trình Guassian) và SMAC (hàm thay thế hồi quy random forest) có chung cấu trúc vấn đề.
Bốn phần của một vấn đề tối ưu hóa mà chúng ta phát triển ở đây sẽ áp dụng cho tất cả các thư viện chỉ với một vài thay đổi về cú pháp. Các phương thức tối ưu hóa được áp dụng cho Gradient Boosting Machine sẽ dịch sang các mô hình học máy khác hoặc bất kỳ vấn đề nào mà chúng ta phải giảm thiểu hàm mục tiêu.

2.3. Gradient Boosting Machine

Chúng ta sẽ sử dụng mô hình học máy Gradient Boosting (GBM) làm mô hình của chúng ta để điều chỉnh trong thư viện LightGBM. GBM là lựa chọn cho mô hình của chúng ta vì nó hoạt động rất tốt đối với các vấn đề kiểu này (như được hiển thị trên leaderboard) và bởi vì hiệu suất của nó phụ thuộc rất nhiều vào việc lựa chọn các giá trị hyperparameter.

2.4. Cross Validation với Early Stopping

Giống như grid search và random search, chúng ta sẽ đánh giá từng bộ hyperparameters bằng cách sử dụng xác thực chéo 5 lần (5 fold cross validation) trên dữ liệu train.
Mô hình GBM sẽ được train với việc sử dụng Early Stopping, trong đó các công cụ ước tính được thêm vào ensemble cho đến khi validation score không giảm trong 100 lần lặp (công cụ ước tính được thêm vào-estimators added).

2.4. Bộ dữ liệu và phương pháp tiếp cận

Như trước đây, chúng ta sẽ làm việc với một phần giới hạn của dữ liệu - 10000 quan sát để train và 6000 quan sát để thử nghiệm.
Điều này sẽ cho phép quá trình tối ưu hóa hoàn thành trong một khoảng thời gian hợp lý.

Sau đó trong notebook, tôi sẽ trình bày kết quả từ 1000 lần lặp tối ưu hóa siêu tham số Bayes trên tập dữ liệu rút gọn và sau đó chúng ta sẽ xem các kết quả sẽ thế nào nếu chuyển thành tập dữ liệu đầy đủ.

Các hàm được phát triển ở đây có thể được lấy và chạy trên bất kỳ tập dữ liệu nào, hoặc được sử dụng với bất kỳ mô hình học máy nào (chỉ với những thay đổi nhỏ trong chi tiết) và làm việc với một tập dữ liệu nhỏ hơn sẽ cho phép chúng ta tìm hiểu tất cả các khái niệm.

Với các khái niệm nền tảng ở trên, hãy bắt đầu với tối ưu hóa Bayes được áp dụng để điều chỉnh hyperparameter tự động!

# Data manipulation
import pandas as pd
import numpy as np

# Modeling
import lightgbm as lgb

# Evaluation of the model
from sklearn.model_selection import KFold, train_test_split
from sklearn.metrics import roc_auc_score

# Visualization
import matplotlib.pyplot as plt
import seaborn as sns

plt.rcParams['font.size'] = 18
%matplotlib inline

# Governing choices for search
N_FOLDS = 5
MAX_EVALS = 5

Đoạn code dưới đây đọc dữ liệu và tạo một phiên bản nhỏ hơn để training và một bộ để testing. Chúng ta có thể chỉ sử dụng dữ liệu train một lần duy nhất khi chúng ta đánh giá mô hình cuối cùng. Điều chỉnh Hyperparameter phải được thực hiện trên dữ liệu training bằng cách sử dụng xác nhận chéo(cross validation)!

features = pd.read_csv('../input/home-credit-default-risk/application_train.csv')

# Sample 16000 rows (10000 for training, 6000 for testing)
features = features.sample(n = 16000, random_state = 42)

# Only numeric features
features = features.select_dtypes('number')

# Extract the labels
labels = np.array(features['TARGET'].astype(np.int32)).reshape((-1, ))
features = features.drop(columns = ['TARGET', 'SK_ID_CURR'])

# Split into training and testing data
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size = 6000, random_state = 42)

print('Train shape: ', train_features.shape)
print('Test shape: ', test_features.shape)
# Train shape:  (10000, 104)
# Test shape:  (6000, 104)
train_features.head()

2.5. Baseline Model

Đầu tiên chúng ta có thể tạo một mô hình với giá trị mặc định của hyperparameters và score it bằng cách sử dụng cross validation với early stopping. Sử dụng hàm cv LightGBM yêu cầu tạo Bộ dữ liệu.

model = lgb.LGBMClassifier(random_state=50)

# Training set
train_set = lgb.Dataset(train_features, label = train_labels)
test_set = lgb.Dataset(test_features, label = test_labels)

# Default hyperparamters
hyperparameters = model.get_params()

# Using early stopping to determine number of estimators.
del hyperparameters['n_estimators']

# Perform cross validation with early stopping
cv_results = lgb.cv(hyperparameters, train_set, num_boost_round = 10000, nfold = N_FOLDS, metrics = 'auc', 
           early_stopping_rounds = 100, verbose_eval = False, seed = 42)

# Highest score
best = cv_results['auc-mean'][-1]

# Standard deviation of best score
best_std = cv_results['auc-stdv'][-1]

print('The maximium ROC AUC in cross validation was {:.5f} with std of {:.5f}.'.format(best, best_std))
print('The ideal number of iterations was {}.'.format(len(cv_results['auc-mean'])))

# The maximium ROC AUC in cross validation was 0.70867 with std of 0.02098.
# The ideal number of iterations was 33.

Bây giờ chúng ta có thể đánh giá mô hình cơ sở trên dữ liệu thử nghiệm.

# Optimal number of esimators found in cv
model.n_estimators = len(cv_results['auc-mean'])

# Train and make predicions with model
model.fit(train_features, train_labels)
preds = model.predict_proba(test_features)[:, 1]
baseline_auc = roc_auc_score(test_labels, preds)

print('The baseline model scores {:.5f} ROC AUC on the test set.'.format(baseline_auc))
# The baseline model scores 0.71466 ROC AUC on the test set.

2.6. Objective Function (hàm mục tiêu)

Phần đầu tiên để viết là hàm mục tiêu nhận một tập hợp các giá trị hyperparameter và trả về cross validation score trên dữ liệu huấn luyện.

Hàm mục tiêu trong Hyperopt phải trả về một giá trị thực duy nhất để giảm thiểu hoặc một từ điển với khóa key "loss" với score để giảm thiểu (và khóa key "status" cho biết liệu lần chạy có thành công hay không).

Tối ưu hóa thường là tối thiểu hóa một giá trị và bởi vì metric của chúng ta là Receiver Operating Characteristic Area Under the Curve (ROC AUC) ,nơi cao hơn sẽ là tốt hơn, hàm mục tiêu sẽ trả về 1−ROC AUC Cross Validation.

Thuật toán sẽ cố gắng điều khiển giá trị này càng thấp càng tốt (tăng ROC AUC) bằng cách chọn các hyperparameters kế tiếp theo dựa trên các kết quả trong quá khứ.

Hàm mục tiêu hoàn chỉnh được hiển thị dưới đây. Cũng như tìm kiếm ngẫu nhiên và tìm kiếm lưới, chúng ta sẽ ghi vào tệp csv trên mỗi lệnh gọi của hàm để theo dõi kết quả theo tiến trình tìm kiếm và do đó chúng ta có bản ghi lưu của quá trình tìm kiếm. (Logic của mẫu phụ và boosting_type sẽ được giải thích khi chúng ta get to the domain).

import csv
from hyperopt import STATUS_OK
from timeit import default_timer as timer

def objective(hyperparameters):
    """Objective function for Gradient Boosting Machine Hyperparameter Optimization.
       Writes a new line to `outfile` on every iteration"""
    
    # Keep track of evals
    global ITERATION
    
    ITERATION += 1
    
    # Using early stopping to find number of trees trained
    if 'n_estimators' in hyperparameters:
        del hyperparameters['n_estimators']
    
    # Retrieve the subsample
    subsample = hyperparameters['boosting_type'].get('subsample', 1.0)
    
    # Extract the boosting type and subsample to top level keys
    hyperparameters['boosting_type'] = hyperparameters['boosting_type']['boosting_type']
    hyperparameters['subsample'] = subsample
    
    # Make sure parameters that need to be integers are integers
    for parameter_name in ['num_leaves', 'subsample_for_bin', 'min_child_samples']:
        hyperparameters[parameter_name] = int(hyperparameters[parameter_name])

    start = timer()
    
    # Perform n_folds cross validation
    cv_results = lgb.cv(hyperparameters, train_set, num_boost_round = 10000, nfold = N_FOLDS, 
                        early_stopping_rounds = 100, metrics = 'auc', seed = 50)

    run_time = timer() - start
    
    # Extract the best score
    best_score = cv_results['auc-mean'][-1]
    
    # Loss must be minimized
    loss = 1 - best_score
    
    # Boosting rounds that returned the highest cv score
    n_estimators = len(cv_results['auc-mean'])
    
    # Add the number of estimators to the hyperparameters
    hyperparameters['n_estimators'] = n_estimators

    # Write to the csv file ('a' means append)
    of_connection = open(OUT_FILE, 'a')
    writer = csv.writer(of_connection)
    writer.writerow([loss, hyperparameters, ITERATION, run_time, best_score])
    of_connection.close()

    # Dictionary with information for evaluation
    return {'loss': loss, 'hyperparameters': hyperparameters, 'iteration': ITERATION,
            'train_time': run_time, 'status': STATUS_OK}

2.7. Domain

Chỉ định tên miền (được gọi là không gian trong Hyperopt) khó hơn một chút so với grid search. Trong Hyperopt và các frameworks tối ưu hóa Bayes khác, miền không phải là một lưới riêng / không liền nhau mà thay vào đó có các phân phối xác suất cho mỗi hyperparameter.

Đối với mỗi hyperparameter, chúng ta sẽ sử dụng các giới hạn giống như với lưới, nhưng thay vì được xác định tại mỗi điểm, the domain đại diện cho xác suất cho mỗi hyperparameter.

Điều này có thể sẽ trở nên rõ ràng hơn trong code và hình ảnh!

from hyperopt import hp
from hyperopt.pyll.stochastic import sample

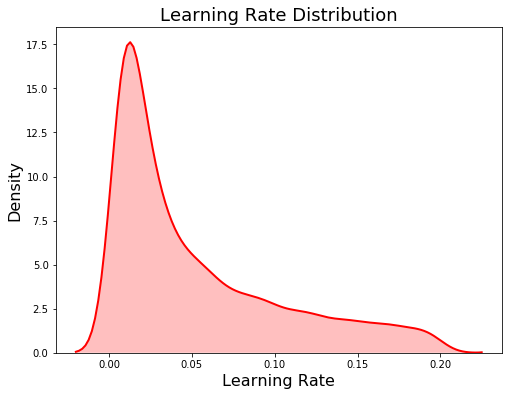
Đầu tiên chúng ta sẽ đi qua một ví dụ về learning rate.
Chúng tôi đang sử dụng một log-uniform space cho learning rate được xác định từ 0,005 đến 0,5. Phân phối log - uniform có các giá trị được đặt đồng đều trong không gian logarit hơn là không gian tuyến tính.
This is useful for variables that differ over several orders of magnitude such as the learning rate.

Ví dụ: với phân phối log-uniform, sẽ có cơ hội bằng nhau để rút ra một giá trị từ 0,005 đến 0,05 và từ 0,05 đến 0,5 (trong không gian tuyến tính, nhiều giá trị sẽ được rút ra từ sau vì khoảng cách tuyến tính lớn hơn nhiều. Không gian logarit hoàn toàn giống nhau - hệ số 10). (in linear space far more values would be drawn from the later since the linear distance is much larger. The logarithmic space is exactly the same - a factor of 10).

# Create the learning rate
learning_rate = {'learning_rate': hp.loguniform('learning_rate', np.log(0.005), np.log(0.2))}
learning_rate_dist = []

# Draw 10000 samples from the learning rate domain
for _ in range(10000):
    learning_rate_dist.append(sample(learning_rate)['learning_rate'])
    
plt.figure(figsize = (8, 6))
sns.kdeplot(learning_rate_dist, color = 'red', linewidth = 2, shade = True);
plt.title('Learning Rate Distribution', size = 18); plt.xlabel('Learning Rate', size = 16); plt.ylabel('Density', size = 16);

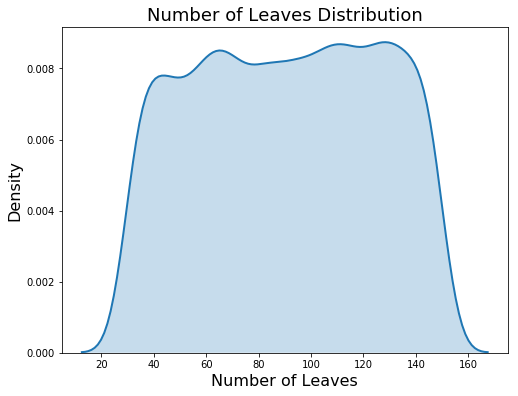
The number of leaves on the other hand is a discrete uniform distribution.

# Discrete uniform distribution
num_leaves = {'num_leaves': hp.quniform('num_leaves', 30, 150, 1)}
num_leaves_dist = []

# Sample 10000 times from the number of leaves distribution
for _ in range(10000):
    num_leaves_dist.append(sample(num_leaves)['num_leaves'])
    
# kdeplot
plt.figure(figsize = (8, 6))
sns.kdeplot(num_leaves_dist, linewidth = 2, shade = True);
plt.title('Number of Leaves Distribution', size = 18); plt.xlabel('Number of Leaves', size = 16); plt.ylabel('Density', size = 16);