Aidemy 2020/11/10
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、異常検知入門の二つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・k近傍法による異常検知
・1クラスSVMによる異常検知
・方向データに対する異常検知
k近傍法
k近傍法とは
(k近傍法は以前にも学習したが、今回は異常検知に即して改めて学習していく)
・k近傍法__とは「判別したいデータとの距離が近い__k個のデータの中の異常データの割合から__異常度を計算する」と言うものである。異常かどうかの判定は、ホテリング法と同様に__閾値を超えているかどうか__で判断する。
・この時の__kが1__であるk近傍法のことを「最近傍法」という。k=1とは、つまり__一番近いデータのみを参照する__という意味である。
・前回のホテリング法には、前提条件として「データが単一の正規分布から発生している」「データ中に異常値をほとんど含まない」と言うことがあった。しかし、今回の__k近傍法ではこのような制約はない。
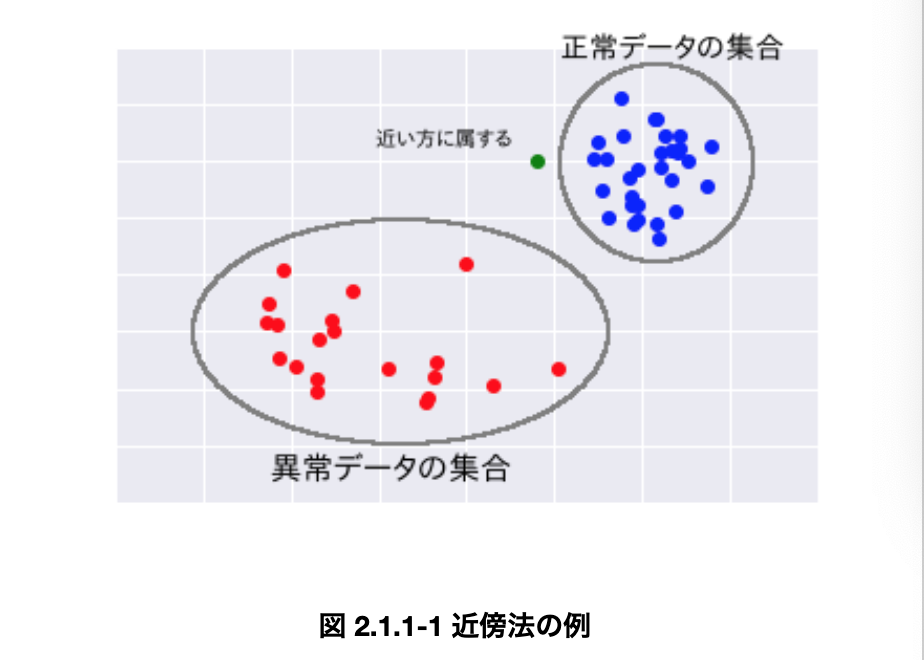
・k近傍法は図示すると非常にわかりやすい。以下の図の緑色の点が正常か異常かを判断する時、正常なデータの集合である青色の集合に近いので、このデータは__「正常」__ということになる。
・k近傍法のメリットとしては、__「データ分布の前提条件がいらない」「正常なデータが複数の集合からできていても使用できる」「異常度の式が簡単」というものが挙げられる。
・一方デメリットとしては、「データ分布の前提条件がないため、閾値が数式で求められない」「パラメータkの厳密なチューニングは複雑な数式が必要」「事前にモデルを作成しない怠惰学習のため、新規データに対する分類の手間が大きい」__というものが挙げられる。
k近傍法の異常度
・k近傍法の異常度は、以下の式で算出される。
$$
\ln \frac{\pi_0 N^1 (x)}{\pi_1 N^0(x)}
$$
・各変数について
・$\pi_0$ は__全標本中の正常なデータの割合__、 $\pi_1$ は__全標本中の異常なデータの割合__
・$N^0 (x)$ は $x$ の $k$ 近傍中の正常なデータの割合、 $N^1 (x)$ は $x$ の $k$ 近傍中の異常なデータの割合
・$\ln$ は自然対数 $e$ を底とする__対数__($\log_e$)
・このそれぞれの値について算出していく。データのラベルを「y」とすると、$\pi_0$は__「y[y == 0].size / y.size」で求められる。すなわち「正常なデータのラベル/全データのラベル」が$\pi_0$である。
・また、$N^0 (x)$は、まず以下のように近傍のラベル「neighbors」を求め、「neighbors[neighbors == 0].size / k」__で算出できる。
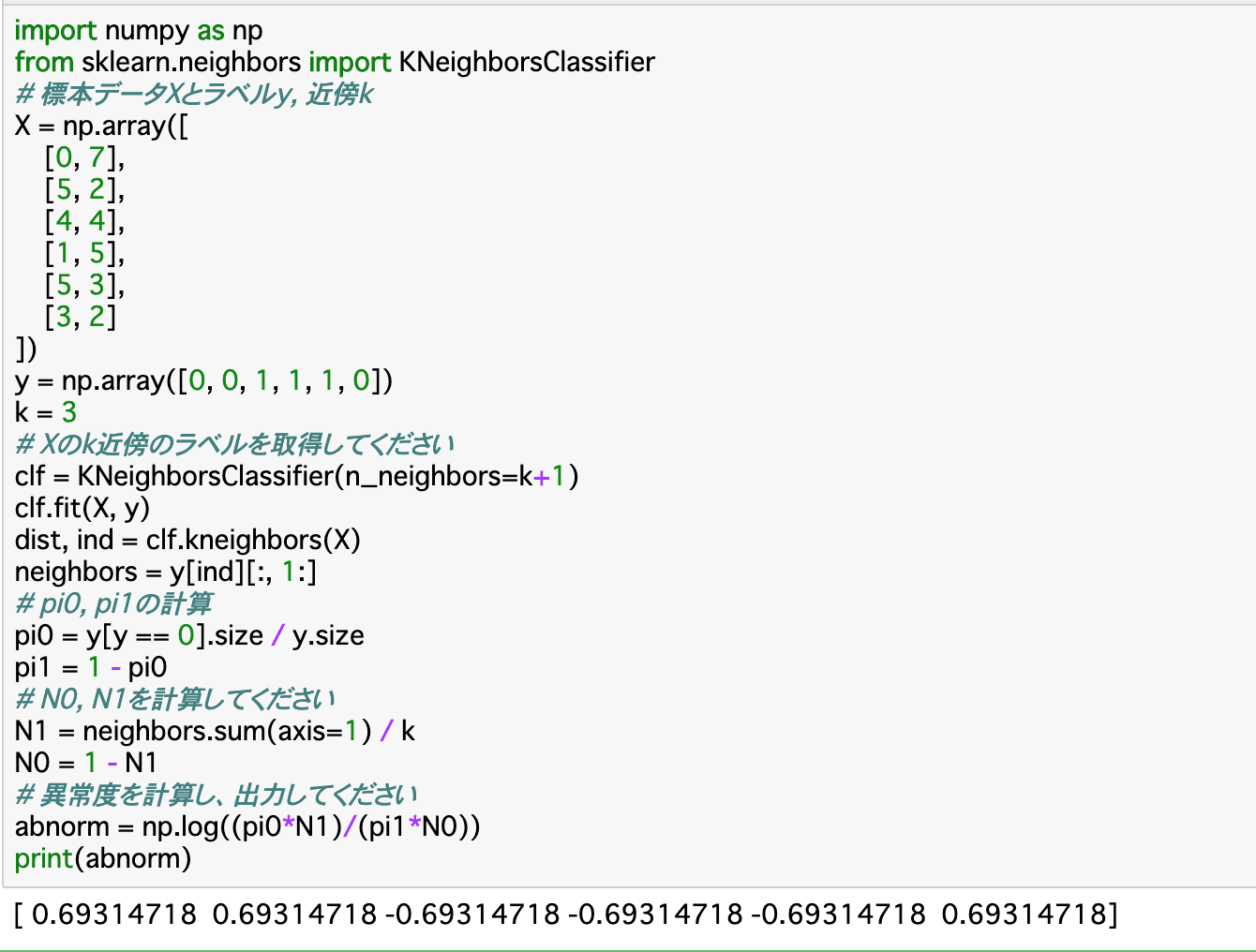
・ここまでで算出した変数を使って異常度を算出する。上記の式の通りにコードを記述するので、次のように表せる。
np.log((N1*pi0)/(N0*pi1))
精度の確認
・N個のデータのうちN-1個を学習させ、残り1個をテストデータとして使ってモデルの精度を確認する方法__を「一つ抜き交差確認法」という。今回はこれを使って精度評価を行う。
・一つ抜き交差確認法は__KNeighborsClassifier__で実装できる。
・コード的には、前項のようにデータを学習させて「neighbors」を算出して異常度を計算する、というように行うが、「kを一つ増やす」「最近傍を除外する」という二つの処理が加わる。
・「kを一つ増やす」については、KNeighborsClassifier()に渡す「n_neighbors」を「k+1」とすれば良い。
・「最近傍を除外する」については、「neighbors」算出の際に、[:, 1:]で__配列の一列目を除外すれば良い。
閾値の設定
・先述の通り、閾値は計算では求められない__ので、自分で設定する必要がある。また、近傍点kも自分で設定しなくてはならない__ので、この2つの__最適値を探すメソッドを作成する。
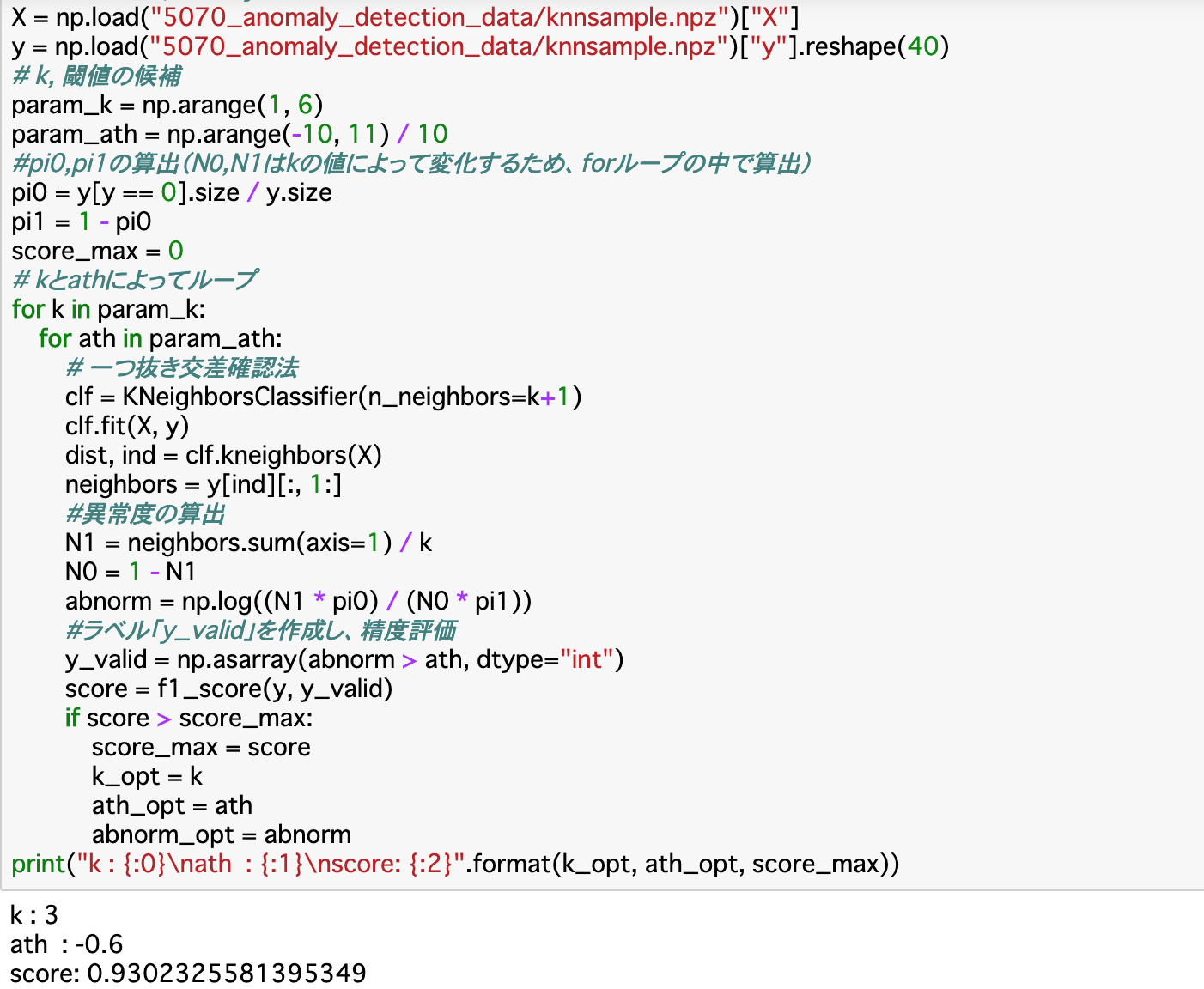
・最適値かどうかは、モデルの精度(F値)を見れば良い。あらかじめkの候補(param_k)と閾値の候補(param_ath)をリストで準備しておき、これらを__forループで取り出して__前項の異常値を算出して閾値と比較し、精度が最大だったら更新するという手法で行う。
・精度の算出については前項の「一つ抜き交差確認法」で行う。また、異常度と閾値の比較の結果、「異常」と判定されたものを「1」それ以外を「0」とする配列を作成する__。このような条件で0,1を分類する配列は__「np.asarray(条件式)」で作成できる。
・精度(score)は「f1_score(y, y_valid)」__でF値を算出することで行える。
・以下では、kの候補を「1〜5」、閾値の候補を「0を中央値として、0.1刻みに21個」として実装する。閾値の候補は__0を中央値とすれば良い__が、kの候補については先述の通り厳密に定めるのは困難である。よって、今回は候補を上記のように挙げる。
異常判定
・前項でも行ったが、K近傍法で異常かどうかを判定するときには__「np.asarray()」__の引数に、「異常値が閾値より大きい」という条件式を設定すると、「0」が正常、「1」が異常の配列が作成される。
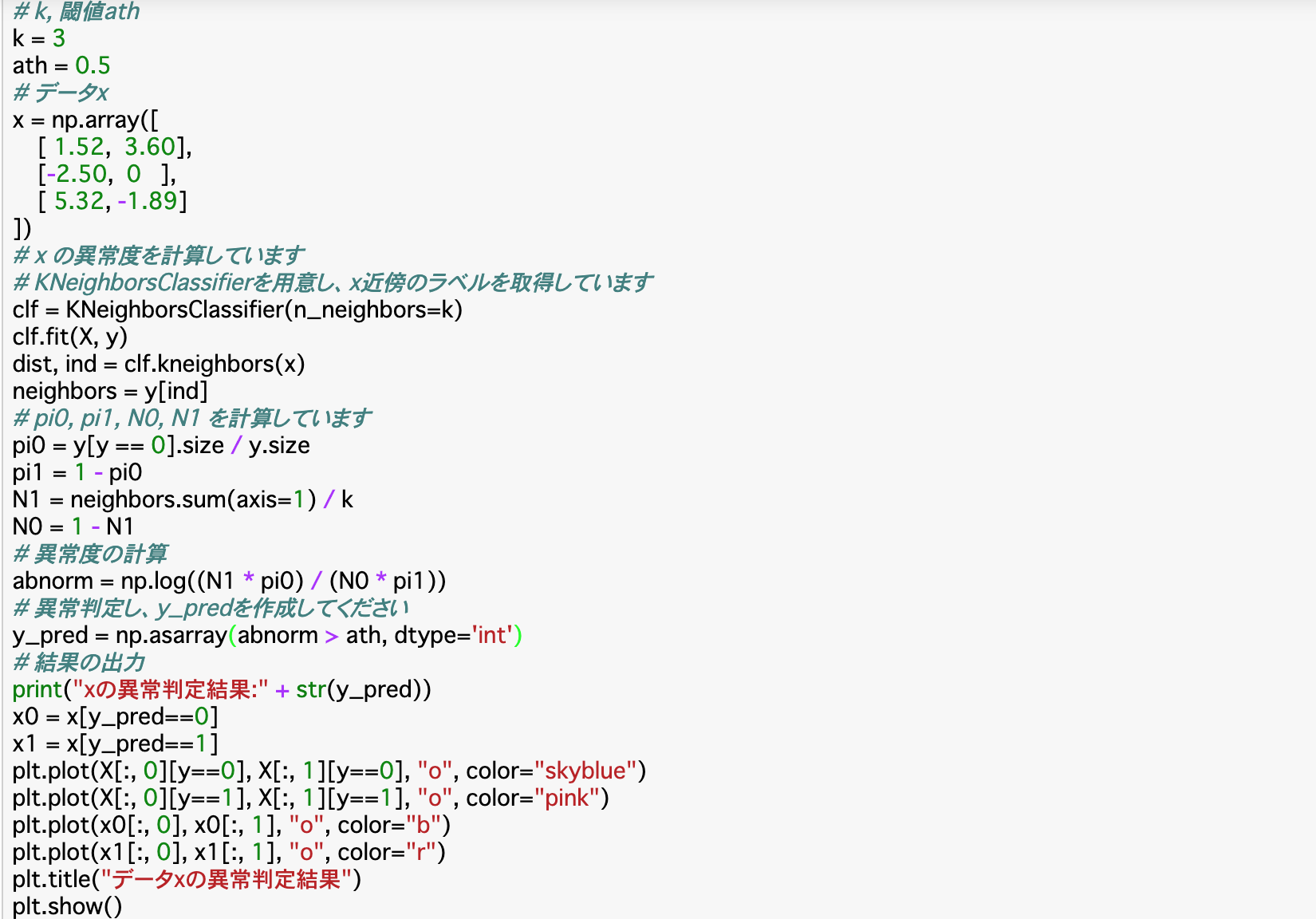
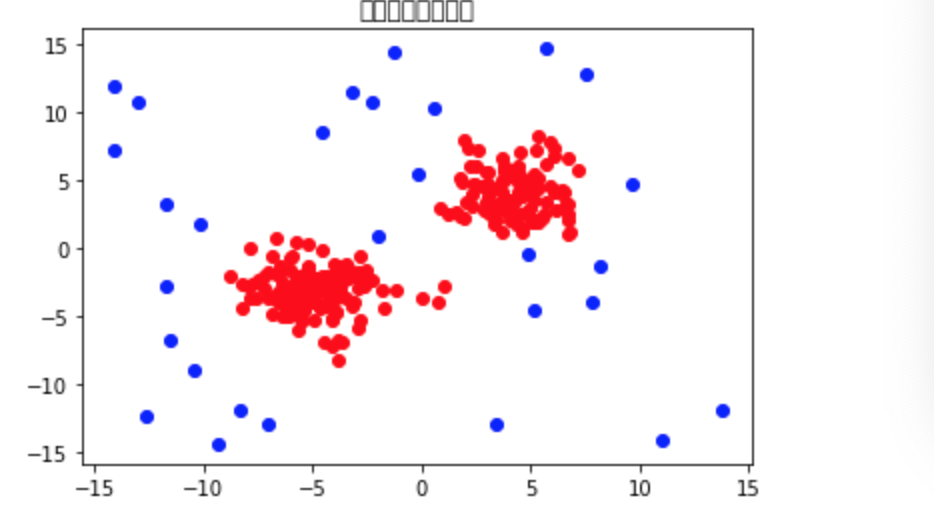
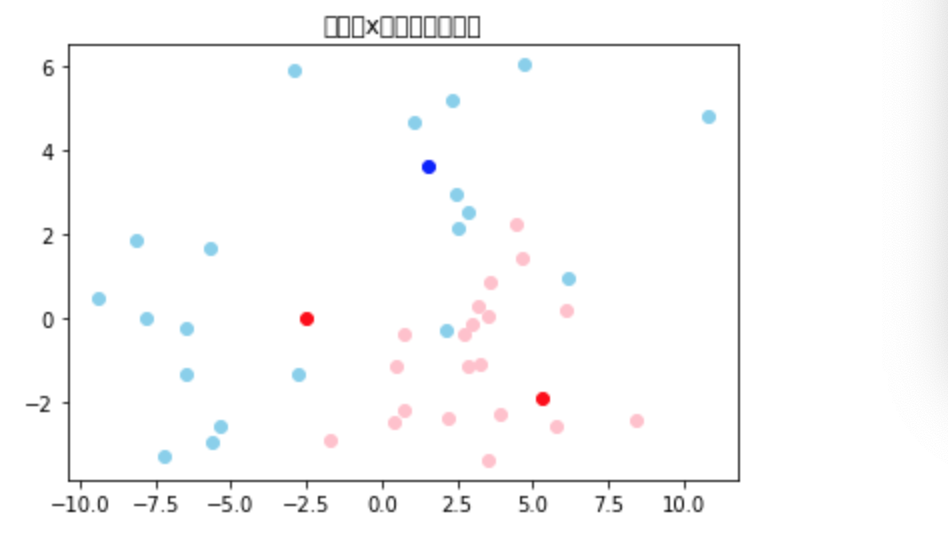
・以下のコードは、前項の処理によって最適なkと閾値を見つけた上で、それを使ってxの異常度を算出し、グラフに表したものである。
・グラフ(赤が異常、青が正常と判定されたもの、薄い色はそれぞれトレーニングデータの分類を表す)
1クラスSVM
1クラスSVMとは
・1クラスSVM__は「ラベルがないデータ」__において外れ値を検出する手法である。つまり、教師なし学習__である。
・ホテリング法をはじめとする外れ値検出の根本的な考え方は、「データのほぼ全てを囲めるような球を作成し、そこから外れたものを外れ値とする」__というものである。ホテリング法では、これを__マハラノビス距離__で行ったが、1クラスSVMでは、「データ空間を歪ませることで__全データを球のなかに入るようにする」ことを通して外れ値を検出する。
・この球を作成するとき、最も外側にあるデータは球面上に存在することになり、これをもとに球が作成される。このことから、この外側にあるデータのことを「サポートベクトルデータ」__と呼ぶ。1クラスSVMではこれを求めることで正常と異常を分ける。
・1クラスSVMの流れは以下のようになる。
①SVMの識別器を作成し、__異常度__を計算
②異常の割合を設定し、閾値__を決定
③閾値と異常値から__異常判定
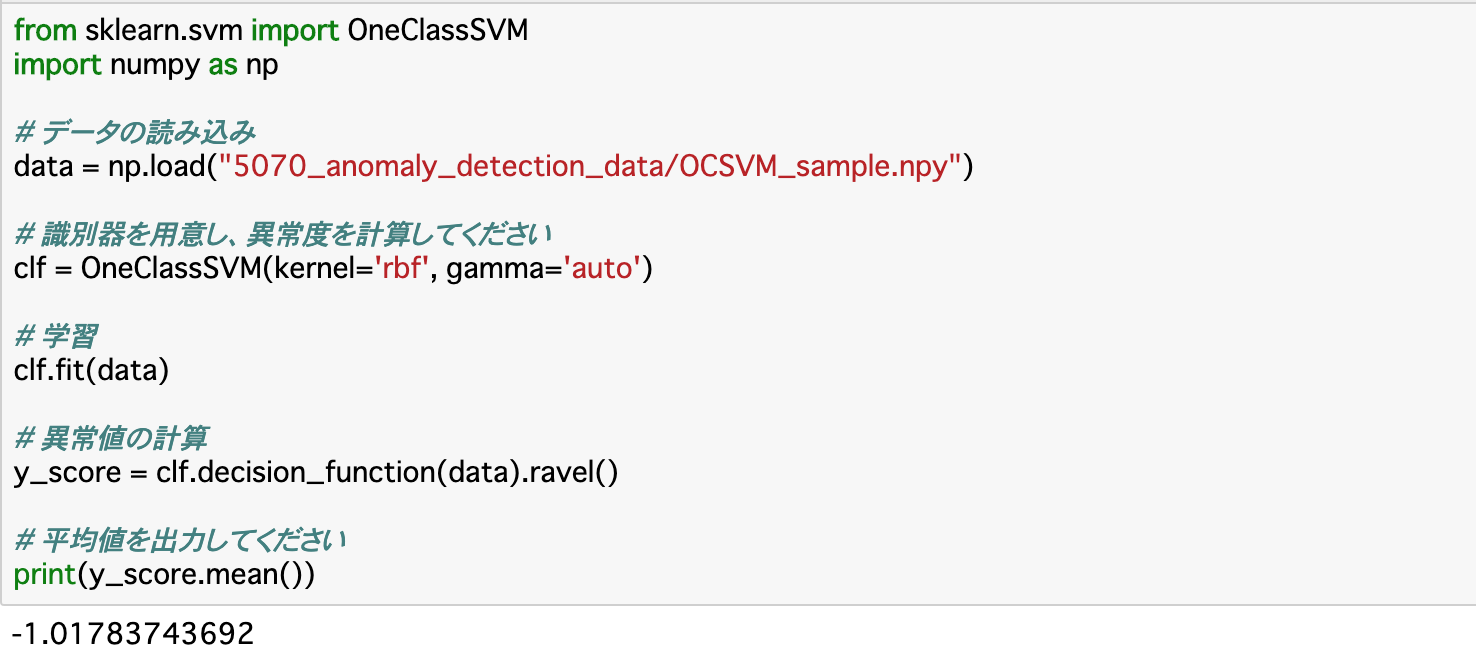
①SVMの識別器を作成し、異常度を計算
・まずはSVMの識別器を作成する。これは__「OneClassSVM()」で作成することが可能である。パラメータとして、「kernel」「gamma」を設定する必要がある。
・「kernel」は__どのように空間を歪めるか__を指定する。基本的には「'rbf'」と指定する。そして'rbf'と指定したときは「gamma」に「'auto'」と指定すれば良い。
・以下ではこのSVMの識別器で異常度を算出していく。算出は「clf.decision_function()」にデータを渡すことで行える。また、算出したもの(多次元データ)は「ravel()」を使って__一次元に変形する。
・1クラスSVMで算出した異常度は、__値が小さいほど異常である__ことを示す。
②異常の割合を設定し、閾値を決定
・次に、閾値__を設定する。ただし、1クラスSVMでは「データには一定の割合で異常データがある」と仮定して閾値を設定する必要がある。以下では、この割合を「a(%)」で表す。
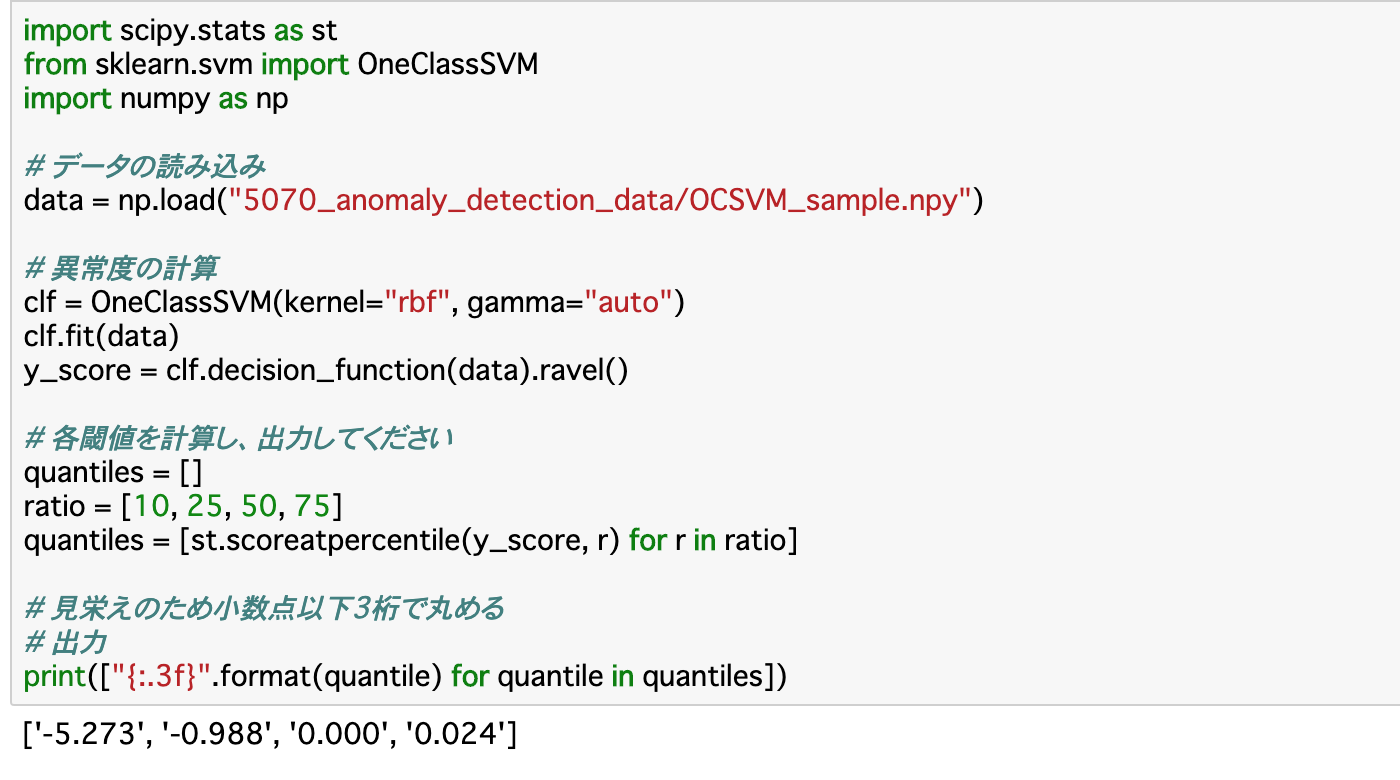
・閾値は「st.scoreatpercentile()」__で求められる。第一引数には、前項で作成した__異常度__を渡し、第二引数には__異常データの割合「a」__を渡す。これにより、異常データが全体のa%となるように閾値が設定される。
・以下のコードでは、異常の割合を「10,25,50,75(%)」として、それぞれの閾値を出力する。
③閾値と異常値から異常判定
・最後に、異常値と閾値を比較して異常判定を行えば良い。実行方法はK近傍法と同様に行えば良い。(今回は(0,1)ではなく__(True,False)__で判断している)
方向データについて異常検知を行う
方向データとは
・例えばある文書データについて、10単語のデータと100単語のデータでは、データのベクトルとしての大きさが異なるため、分類などがうまくできない時がある。このようなときに__データの大きさを1に統一する__ことでこの問題を解決する。このことを__「規格化」といい、規格化されたベクトルデータのことを「方向データ」という。
・今回は、この方向データに異常検知を行う。この場合も、1クラスSVMの時と同じで__ラベルなしのデータを扱い、「データが単一方向を中心に分布している」「異常な値をほとんど含まない」という制約がある。
・流れは以下のようになる。
①データの__規格化
②データの__異常度計算
③標本の分布から__閾値を設定__
④__異常判定__
①データの規格化
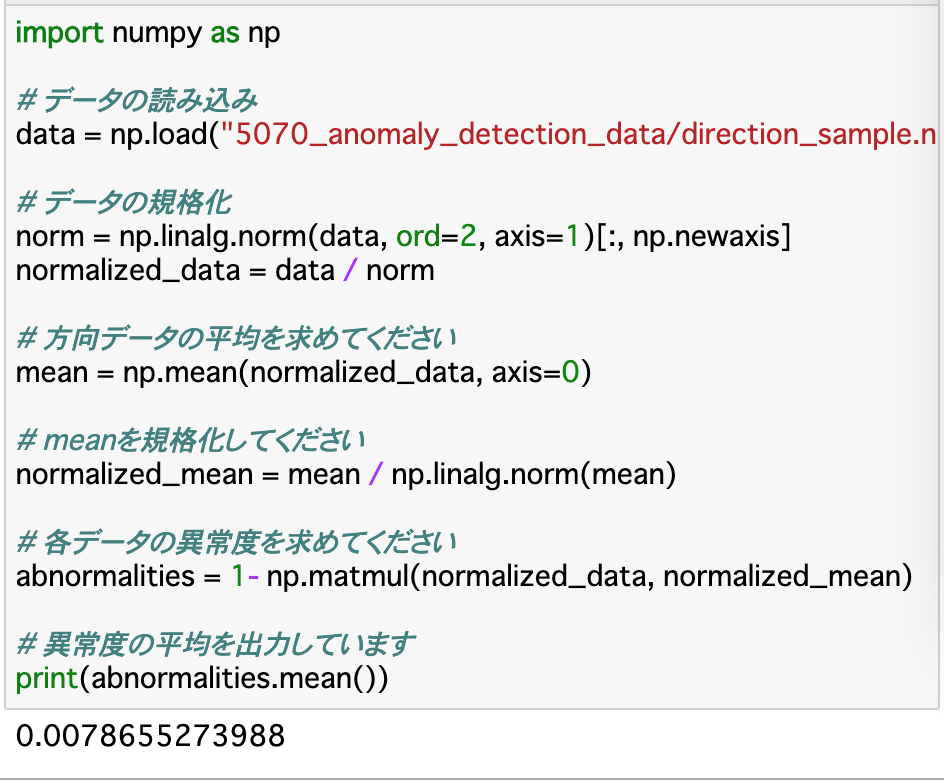
・データの大きさ(長さ)を1にするには、__「データをそのデータ自身の長さでわる」ことで求められる。よって、まずは__データの長さを求める__必要がある。
・データの長さは「np.linalg.norm(data,ord=2,axis=1)[:,np.newaxis]」で求められる。これは深層学習の正則化(過学習を防ぐ処理)でも行った。「ord」は__次元数__の指定(今回は二次元)、「axis」は1、つまり__行方向の長さを算出する__ことを指定している。[:,np.newaxis]__の部分は、規格化する際に、データとの軸を揃えるために調整している。
②データの異常度計算
・方向データは、単一の方向を中心に分布すると仮定しているので、__異常度は、この方向からどれほどずれているか__によって決定する。このズレを規定するには、方向の基準__を決める必要がある。今回は規格化した方向の__平均値__を使う。
・規格化したデータの平均は、そのまま「np.mean()」に、前項で規格化したデータを渡せば良い。この時、「axis=0」で指定する。ただし、この平均について__もう一度規格化を行う必要がある__ので注意する。
・異常度は、「1 - (データと平均したベクトルの内積)」で求めることができる。ベクトル同士の内積は「np.dot()」で求めることができるが、今回のデータはベクトルの集合、すなわち「行列」であるので、そのような時は「np.matmul()」__を使う。使い方はdotと同じ。
③標本の分布から閾値を設定
・異常度は__「χ二乗分布」に従うという定理がある。よって、前項で算出した異常度を使ってデータの分布を求め、そこから閾値を算出する。
・χ二乗分布の使い方についてはChapter1参照。復習にはなるが、実装は「st.chi2.ppf()」で行う。第一引数には「1-誤報率」を渡す。この誤報率は自分で設定する。
・また、今回は、第二引数には「df」、第三引数として「scale」を設定する。「df」には__自由度__を設定する。自由度は「2*異常度の二乗平均 / (異常度の二乗平均 - 異常度の平均の二乗)」で求められる。また、「scale」に設定するものはχ二乗分布のステータスであり、「異常度の二乗平均 / 自由度」__で求めることができる。
④異常判定
・最後に、データの異常判定を行う。ここでは、今までの標本データとは別に用意された__観測データ「X」いついて異常判定を行う__。
・異常判定には、前項で作成した閾値と、Xの異常度を比べる必要があるので、まずは__Xの異常度を算出する__。
・Xの異常度は__「np.matmul()」に「X」と「標本データの平均値」を渡して内積を求めれば良い。
・ここまで終わったら、「np.asarray(条件式)」__で異常か正常かを分類する。
まとめ
・k近傍法__を使った異常検知は「k個のデータの中の異常なデータの割合」が閾値を超えたときに異常と判定される。k近傍法ではホテリング法のような__制約がない__ので、いろいろなデータに対して使うことができる。
・精度評価の一手法として、「一つ抜き交差法」__というものがある。これは、データのうち一つ__を精度評価のためのテストデータにするというものである。
・また__ラベルがないデータ__を異常検知するときに使う手法が「1クラスSVM」__である。SVMを使って異常度の計算を行い、__異常が何割あるか__を事前に設定し、そこから閾値を求めるという手法で異常検知を行う。
・規格化を行ったベクトルデータ、すなわち__方向データ__に対して、ラベルなしの異常検知を行うことができる。異常度はデータと基準になる方向データとの__内積を取る__ことで算出でき、__χ二乗分布__を使うことで閾値を設定する。
今回は以上です。最後まで読んでいただき、ありがとうございました。