強化学習1 入門編

Aidemy　2020/11/15
#はじめに
　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、強化学習の一つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・強化学習とは
・エージェント、環境、報酬
・強化学習の方策

#強化学習とは
・機械学習は大別すると__「教師あり学習」「教師なし学習」「強化学習」に分けられる。
・そのうち、今回学んでいく__強化学習__は、「与えられた条件下で最適な行動を発見すること」__を目的とした手法である。例えばゲームであれば、強化学習によって勝ち方を発見することができる。

##強化学習についての詳細
・強化学習は__「エージェント（player）」と「環境（stage）」__が相互作用するという前提のもとで進められる。
・ある__エージェント__が__状態s__にあるとして、__環境__に対して__行動a__を取るとすると、これによって環境はその行動の評価として__報酬R__を返し、エージェントは__次の状態s'__に移行するということを繰り返しながらタスクを進めていく。
・例えばスーパーマリオの例で言えば、エージェントである「マリオ」が、「先に進んでゴールを目指すが、敵に当たると終了」という環境で、「敵を（ジャンプで）避ける」という行動を取ると、環境は「その先に進める権利（そこでゲームが終わらない）」という報酬を返す。これを繰り返して、マリオはゴールというタスクに向かって進んでいく。

・強化学習においては、その場の報酬__「即時報酬」を最大化するだけでなく、その後に得られる報酬「遅延報酬」も含めた「収益」__を最大化することが必要になる。
・先のマリオの例では、コインを取ることはその場では価値のない行動であるが、100枚集めて「残機を増やす」ことに価値を見出す場合、報酬を最大化するためにはできる限りコインを取るように行動したほうが良いと言える。

##N腕バンディット問題
・N腕バンディット問題__は強化学習の一例で、「N台のスロットマシーンがあり、あたりなら1外れなら0という報酬が支払われるとする。あたりの確率は台ごとに異なるが、ユーザーからは見えない」とするとき、「ユーザーは1回の試行でどれか一つのスロットを引けるとするとき、試行回数当たりの平均報酬量を最大化するにはどうすれば良いか」を考える問題である。
・考え方としては「最も確率の高い台で引く」__ということが理にかなっているが、その台を見つける（推測する）ためにも試行が必要である。というのがこの問題のミソである。
・以降では、この例を使って強化学習について学んでいく。

##エージェントの作成
・エージェント__とは、より詳しくいうと「環境の中で行動を決定し、環境に対して影響を与えるもの」__を指す。
・N腕バンディット問題では、どの台を使うかを判断し、報酬を受け取り、次の判断をする__ユーザー__がエージェントである。
・エージェントが取得した報酬から、どのように次の判断を行うかという指標__のことを「方策」__という。例えば、この問題において方策が「常に1」というようにきまっているとき、エージェントは常に報酬が1となるような台を狙うことになる。
・このエージェントの最適な方策を決定するのが今回の目的である。

・以下のコードは、今回の手法__「どの台を選ぶか」をランダムで決定する関数「randomselect()」である。これによって、どの台を選ぶのかという「slot_num」__が返される。

##環境の作成
・__環境__とは、エージェントが行動を起こす対象__である。役割としては、行動を受けて状況を観測し、報酬をエージェントに送信し、時間を一つ進めるというものがある。
・今回の問題における環境は「エージェントがある台を引いた時、その台の確率によって当たりかはずれかを出すプロセス」__である。

・以下のコードは環境を定義した関数__「environment()」である。「coins_p」で各台の当たる確率をNumPy配列で格納し、「results」には「np.random.binomial(n, p)」で試行回数n、確率pの二項分布を求める関数を使用して、スロットを引いた結果を格納する。今回は試行回数1回で確率は「coins_p」であるので、(1, coins_p)__と指定すれば良い。environment関数としては、渡された「band_number」の結果を返せば良いので、これを「result」に格納して返す。

##報酬の定義
・__報酬（reward）__とは、__エージェントの一連の行動の望ましさを評価する指標__のことである。
・今回の問題で言えば、スロットを引いて得られた__返り値（0or1）__がそのまま報酬である。これは__即時報酬__に当たる。

・以下のコードは報酬を定義した関数__「reward()」である。先ほどのenvironment関数で得た結果を「result」に格納し、引数で渡された配列「record」の現在の試行回数を示す「time」番目にこれを格納する。
・また、[[(台の番号),(選択回数),(報酬合計),(報酬合計÷選択回数)],...]となっているリスト「results」__に、それぞれの結果を格納していく。

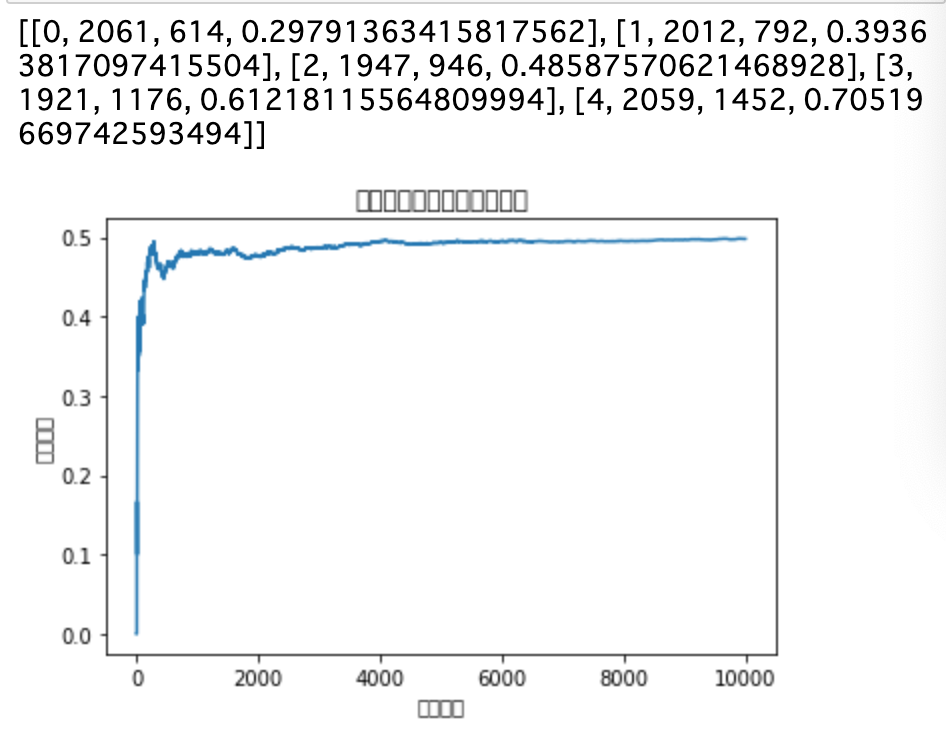
・さらに、これらの関数を使ったり、自分で値を渡したりして__「使う台」「あたりかハズレか」「何回試行するか」__などを決め、それぞれの台の試行回数と結果を出力し、__平均報酬の遷移を図示__したものが以下である。

・結果

・この結果を見ると、「どの台を選ぶか」は完全にランダム（1/5）にしているので、__台が選ばれる回数は均等__で、当たる確率もおよそ設定した値通りになっている。また、グラフから見てわかるように、平均報酬は0.5付近を維持している。

#N腕バンディッド問題の方策
##greedy手法
・ここまででエージェントや環境、報酬の型は定義できたので、次は実際に__「どうやれば平均報酬を上げられるか」__という__方策__を考えていく。
・基本的な方針としては、最初は情報が全くないので、ランダムに台を選ぶしかない。ある程度試行を重ね、台の当たる確率が推測できるようになったら、最も確率の高い台を探し、その台を選び続ける選択を取る__ことにする。
・この時の、ある程度試行を重ねて情報を収集することを「探索」といい、最終的に最適な台を選び続けることを「利用」__という。

・この方針を最も単純に行う手法が__「greedy手法」である。これは、「これまでの結果から最も期待値の大きいものを選択する」という単純明快なものになっている。
・まずは__探索__を行う。この時、一台につきn回試行する__ということをあらかじめ決めておき、それをすべての台について行っていく。これが終了したら、その時点での__報酬の期待値$u{i}$を計算__し、一番大きいものを選択する。
・期待値$u{i}$は「(マシンiの報酬の和)÷(マシンiの試行回数)」__で求められる。

・以下のコードでは、実際にこの手法を定義して、前項までで作成した環境などを定義した関数も使用して試行した例である。

・greedy手法の定義は、まず__「一台の試行回数上限に達するまでslot_numをその台のままにする」というものと、「すべての台が試行回数上限に達したら、slot_numをその時点で最も期待値の高いものにする」というものを定義すれば良い。
・後者について、コードで「np.array()」としているのは、最大値を取得するメソッド「argmax()」__を使うためである。

・値を与えてgreedy手法の実践

・結果

・この結果からわかることとして、与えられた探索のための試行回数の上限__「n=100」まではすべての台について試行を行なっており、そこからは最も期待値の高い「台4」__にすべての試行（残り9500回）を使っている。

##ε（イプシロン）-greedy手法
・前項のgreedy手法は、nが小さいほど、つまり探索に使う試行回数が減るほど、間違った台を選ぶ可能性が高くなってしまう。一方、nを大きくすれば最適な台を選ぶ可能性は高くなるが、探索の方に多くの試行回数を使ってしまい、無駄が大きくなってしまう。
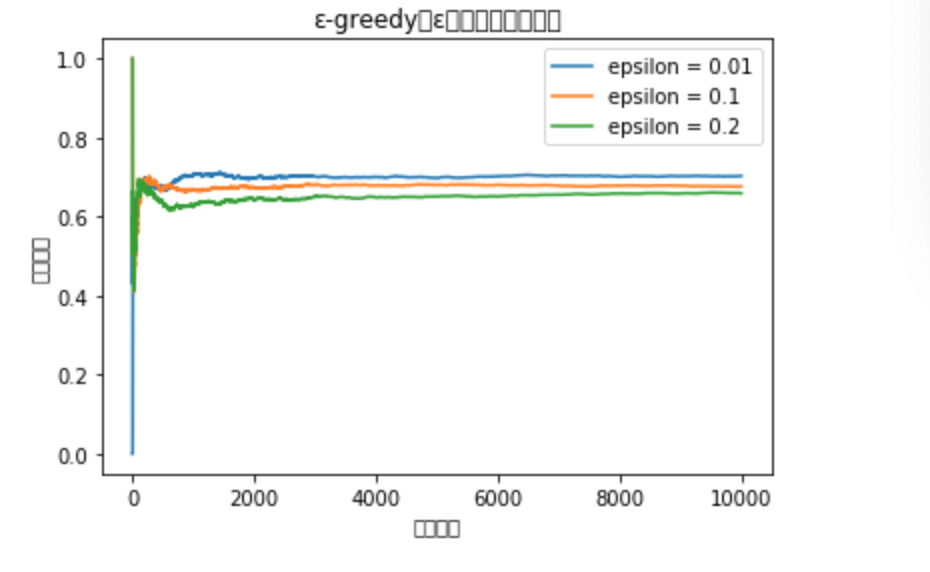
・今回の__「ε-greedy手法」はこの問題点を解消できる。この手法は__探索と利用を織り混ぜる__ことで、探索のコストを減らしつつ間違った台を選び続けるリスクを減らすことができるというものである。
・ε-greedy手法の流れは以下のようになる。
　①まだ選択したことのない台があればそれを選ぶ
　②__確率εで全台からランダムで選択する（探索）
　③__確率1-εでこれまでの報酬平均（期待値）が最大のマシンを選択する__（利用）

・つまり、各試行ごとに、__確率εで探索を行い、確率1-εで利用を行う__というのがこの手法である。

・ε-greedy手法の定義部分

・実行部分

・結果

##楽観的初期値法
・greedy手法では、例えば「0.4と0.6の確率で当たる台A,B」があるとして、「Aの台」の期待値を「0.8」のように多めに予測した場合は、初めはAの台を選び続けるが、試行によって実はAの台は期待値が低そうだ（0.4に収束する）ということを認識し、Bの台に移行していくことができる。
・一方で、「Bの台」の期待値を「0.2」のように__少なめに予測してしまうと__、「Bの台は試行しない」つまり「Aの台しか選ばない」という状況に陥ってしまい、間違いに気づくことができない__という問題点がある。
・このようなリスクを減らす手法として、「不確かな時は期待値を高めに（楽観的に）見積もる」という「楽観的初期値法」__が使われる。
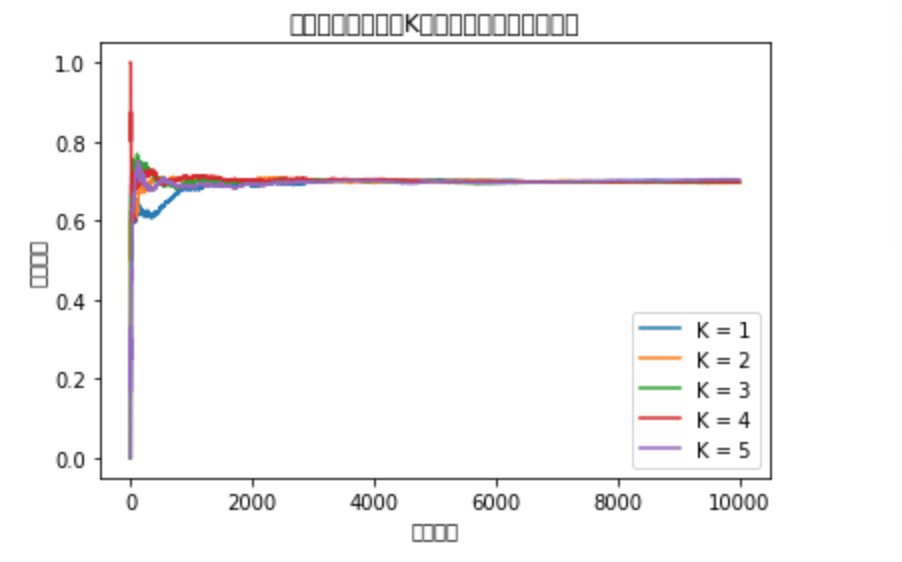
・具体的な考え方としては、学習の前に、各台から報酬の最大値をK回得ていることにしてから期待値を計算する__ということを行う。
・よって、この手法を使う際には「報酬の最大値(rsup)」と「最大値を得たと仮定する回数(K)」_を指定する必要がある。
・この二つを使った各台の期待値は$\frac{R(N)+Kr{sup}}{N + K}$で求められる。__R(N)__は実際に測定した回数（resultsの3列目に格納）、__N__は実際に測定した回数（resultsの2列目に格納）である。よって、コードは以下のようになる。

・実行部分

・結果

##soft-max法
・ε-greedy法では、探索の際に、明らかに最悪と考えられる台であっても、決められた回数は必ず試行してしまう__ことが欠点に挙げられる。例えば当たる確率が20％で、あたりだと「1」ハズレだと「-100」となる台があったとすると、この台を引くことは極めて悪い行動になることが予測されるが、ε-greedy法では、これを避けて探索することはできない。
・これを解消できるのが、「soft-max法」である。これは、「価値の高そうな行動を選ばれやすく、低そうな行動を選ばれにくくする」というものである。つまり、「各行動に重み付け」を行う。
・重みは$\frac{\exp{Q{i}/ \tau}}{\sum^i \exp{Q{i}/ \tau}}$という式を使って算出する。 $Q_i$は報酬の期待値、$\tau$(タウ)はパラメータであり、$\tau$が小さいほど上記重み付けの傾向が強くなる。
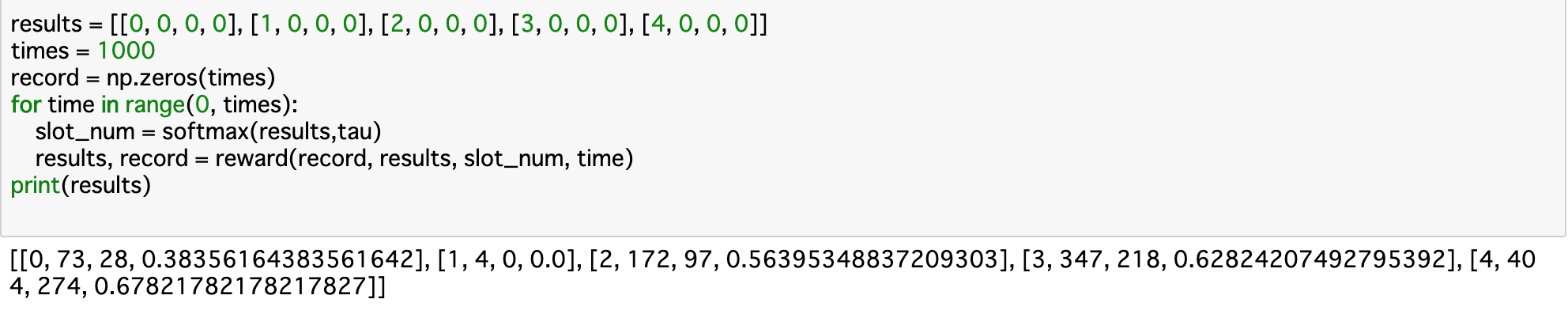
・soft-max法の流れとしては、__データがない場合はすべての報酬を「1」と仮定__し、各台の選択確率を上記の式で算出し、これに基づいて選択を行い、報酬を得ることで報酬関数を更新する、というように行われる。具体的なコードは以下の通り。

・上記コードについて、まずは報酬の予測期待値__「q」を算出する。これはresultsの4列目を参照すれば良い。次に、データがない場合は報酬期待値「q」はすべて「1」とする、すなわちすべての値が1の配列を「np.ones()」で作成する。
・「q」と渡された「tau」を使った上記の式で選択確率「probability」を算出する。そして、確率がprobabilityで、選択される対象は台の番号であるとして、「np.random.choice(配列,p=確率)」__で何が選ばれるかを定義する。

・実行部分

・上記の結果を見てみると、基本的には台の当たる確率通りに選ばれることが多くなっている。ただし、今回の試行では1番の台が全く当たらず、「確率が0の台」とみなされ、それ以降は選ばれていない。

##UCB1アルゴリズム
・__UCB1アルゴリズム__は、楽観的初期値法__を改善した手法である。具体的には、「そのマシンがどれだけ当たってきたか（成功率）」と「そのマシンについてどれだけ知っているか(偶然によるデータのばらつきの大きさ)」を合わせて判断することで、あまり探索されていない台は積極的に探索__し、データが集まってきたら__最も当選確率の高い台を選択する__ということを同時に行うことができる。
・流れとしては、まず__報酬の最大値と最小値の差「R」を算出する。そして、まだ選んだことのない台があればそれを選択し、得られた結果から各台の__報酬の期待値（成功率）「$u{i}$」を計算する。
・また、これらを使った$R\sqrt{\frac{2logT}{N}}$で、各台の偶然によるデータのばらつきの大きさ「$x{i}$」を計算する。この時の「T」は総プレイ回数、「N」はマシンiのプレイ回数を表す。
・この「$u{i}$」と「$x{i}$」の__和__が最大となる台が最適であると考えて、それを選択する。
・以上をコードで表すと以下のようになる。（N腕バンディッドではR=1である）

・上記コードについて、「まだ選んだことのないマシン」は、resultsの1列目（試行回数）が0であるものと言い換えることができる。また、「これまでの総試行回数（times）」はこの部分をすべて「sum()」で足し合わせれば良い。
・各台の偶然によるデータのばらつきの大きさ「xi」は上記の公式通りに記述すれば良いが__「math.sqrt()」でルート、「math.log()」__でlogがそれぞれ表現できる。

・実行部分

・この結果について、どの台も最低限の回数は試行されているが、確率の低そうな台はあまり試行されておらず、無駄が少なくなっている。

##ここまでの手法について
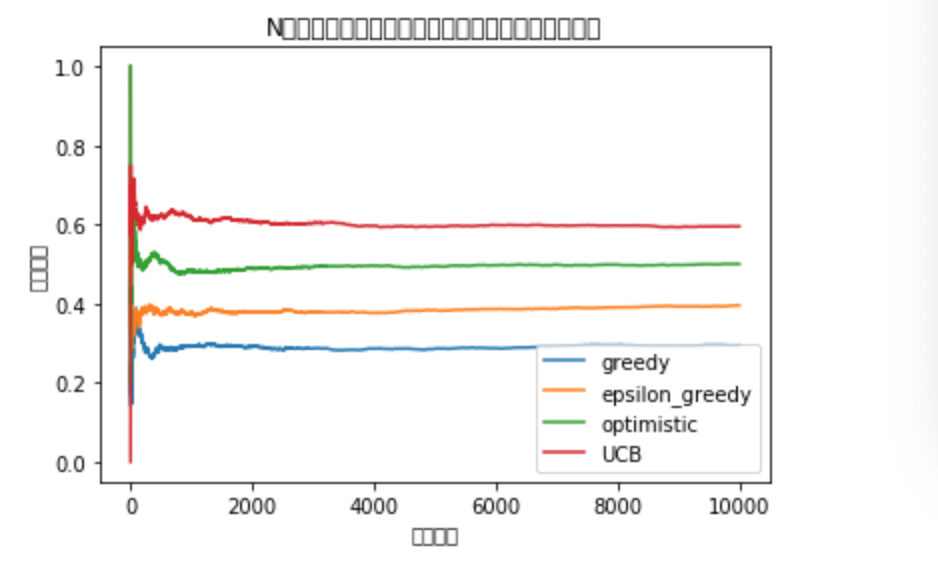
・ここまでで__「greedy手法」「ε-greedy手法」「soft-max手法」「楽観的初期値法」「UCB1アルゴリズム」の五つを見てきたが、明確な優劣はなく、大事なのは__問題によって使い分ける__ということである。
・強化学習の前提として「探索と利用はトレードオフの関係にある」ということが言える。すなわち、探索回数を多くすれば、最適な台以外の試行回数も増えてしまうため無駄が大きくなってしまい、利用回数を多くすれば、最善の台を選ばないリスクが大きくなってしまう。
・例えば全体の試行回数が少ない時は、探索の割合が大きい「ε-greedy法」などは最適な台を見つけやすいため、報酬率が高くなりやすい。一方で、試行回数が多い時は探索の無駄が大きくなってしまうこの手法よりもスマートに探索が行え、利用回数が増える「UCB1アルゴリズム」の方が報酬率が高くなりやすい。
・最初からすべての確率が公表されている時は、エージェントはその中から最適なもののみを試行すれば良い、すなわち探索が必要なくなるが、この時の報酬と、上の五つの手法を使った場合の報酬の差分を「リグレット」と呼ぶ。
・五つの手法の中で、最もリグレットを最小化できるのが「UCB1アルゴリズム」__である。

・各手法の結果を表した図（N腕バンディッド問題の場合）

#まとめ
・強化学習__とは、与えられた条件下で最適な行動を発見することを目的した手法である。
・強化学習では行動者の「エージェント」__が存在する。N腕バンディッド問題__では「台を選ぶ」という行動をとる。
・また、エージェントが行動を起こす対象である「環境」も存在する。この場合の環境は「台があたりかハズレかを返すプロセス」である。
・「報酬」は、エージェントの行動の望ましさを評価する指標のことである。この報酬の大きさを最大化することが強化学習の目的である。
・この報酬を最大化するための手法として「greedy手法」「ε-greedy手法」「soft-max手法」「楽観的初期値法」「UCB1アルゴリズム」が挙げられる。どの手法も、はじめにそれぞれの台の確率を推定するために「探索」を行い、その結果から最適な台を選ぶ「利用」__を行う。

今回は以上です。最後まで読んでいただき、ありがとうございました。