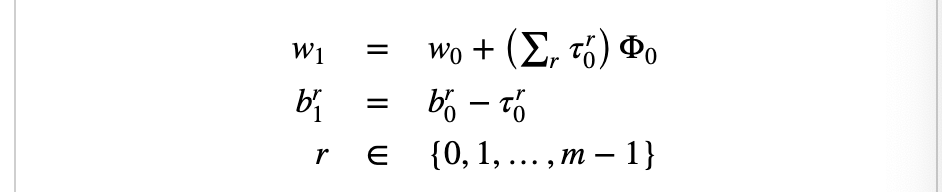Aidemy 2020/12/2
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、ランキング学習の一つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・ランキング学習とは
・特徴ベクトルの成分
・重みベクトルの学習
・ランキング学習の性能評価指標
ランキング学習について
ランキング学習とは
・__ランキング学習__とは、定義した重要度に基づいて__情報を並べる__ための機械学習の手法である。
・短な応用例としては、Google検索などの__検索エンジン__がある。あるキーワードを検索にかけた時、表示される__ページの並び順__はランキング学習によって決められている。さらに発展させると、Siriなどの自動応答システムでも使用されており、重要性が増している。
・このランキング学習を活用することで、重要な情報を素早く認識させることができる。
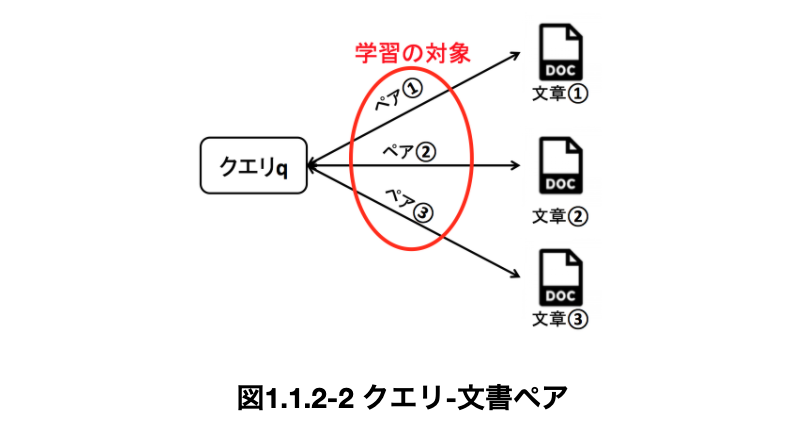
クエリ-文書ペア
・これより先は、__「文書d」を重要な順に並べ替えることを考える。そして、並べ替える時の指標となる、何についての情報が得たいかを指定する__キーワード__のようなものを「クエリq」__という。
・検索エンジンの例で言えば、__検索キーワードがクエリ__として、__ランキング関数__というものと照らし合わされ、__ホームページという文書__を並べ替える操作を行っている。
・クエリに従って文書を適切に並べるためには、クエリと文書がどれぐらい関連しているか__を計算することが必要であるため、機械学習によってこれを求める。この時の教師データは、この関連性を示す「クエリ-文書ペア」__である。
ランキング関数
・__ランキング関数__とは、与えられたクエリに基づいて__文書の重要度を決定するための関数__である。
・もっとも基本的には、__特徴ベクトルと重みベクトルの内積__によって定義されるものである。Chapter1とChapter2ではこれをランキング関数として進めていく。
・特徴ベクトル__について、これは__文書の特徴量を成分とするベクトル__であり、「クエリ依存型」と「クエリ非依存型」__がある。これらはそれぞれ成分として、__クエリと文書の結びつき__や、__文書自体の持つ重要性__を指す。
・クエリ依存型__は、クエリ(検索ワード)と文書(ホームページ)を比較して計算する要素であり、「TF,IDF,BM25」__といったものがある。
・__クエリ非依存型__は、クエリ取得前から、あらかじめ計算されている要素である。例で言うと、サイトやページに対して、集まっているリンクをもとに、人気順に求めておくことができる。具体的には__PageRank__などがある。
・重みベクトル__について、これは特徴ベクトルの成分に__重みをつけるベクトル__である。前述したように、ランキング関数は特徴ベクトルと重みベクトルの内積で表されるので、「クエリ-文書ペアが持つ特徴量の線型結合」__と言うことができる。
特徴ベクトルの成分
TF
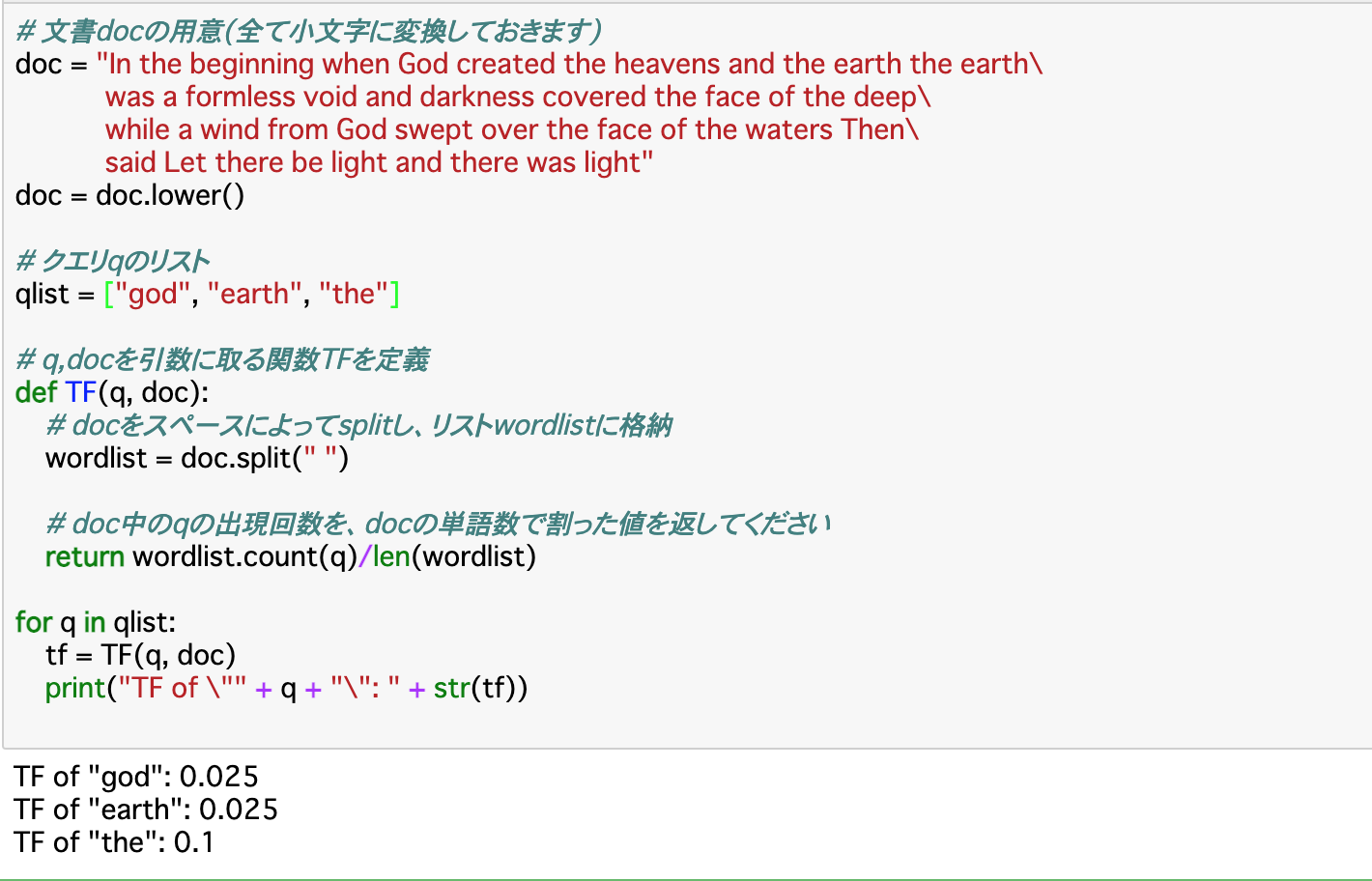
・前項で示した__特徴ベクトル__の成分の一つとして挙げられるのが、__「TF(Term Frequency)」__である。TFは__文書中の単語のうちクエリの割合__を示す。検索であれば、ホームページ内に検索したワードがたくさんあれば、TFの値は大きくなる。
・すなわち、クエリqと文書dに対する__TF(q,d)は「クエリ数÷全単語数」で求められる。以下では実際にTFを算出している。クエリ数は「wordlist.count(クエリ)」で、全単語数は「len(wordlist)」__で求められる。
IDF
・特徴ベクトルの成分の2つ目は__「IDF(Inverse Document Frequency)」__である。これは、__総文書数Dに対して、クエリqが含まれる文書dの数が少ないほど、値が大きくなる__と言うものである。すなわち、__あるクエリqがどれぐらい珍しいか__を示す指標であると言える。計算式は以下の通りである。
$$IDF(q)=log(\frac{D}{d})+1$$
・上記式について、$log(\frac{D}{d})$としているのは、特にdが小さい時、例えばd=1であるときとd=2であるとき、対数を取らないと値が2倍も変わってしまうから__である。文書の数は1つしか違わないのに、希少性が2倍も違うと言うのは極端なので、対数を取ることでこのような結果にならないようにしている。
・以下では、実際に文書D中の任意のクエリqを渡すことでIDFの値を計算してくれる関数「IDF()」__を作成し、「light」「a」「to」についてIDFの値を求めている。(文書は前項のような感じだが、長いので割愛)
BM25
・__BM25__は、__TFとIDFと、新しいNDL__の3つの指標を組み合わせた__合成指標__である。__NDL(Normalized Document Length)__は、__ある文書dが、全文書の平均の長さに比べてどれぐらいの長さか__を示す指標である。文書dが短いほどNDLの値は大きくなる。
・NDLは、ある文書を$d_k$とし、全文書の長さの平均を$\overline{DL}$とすると、以下のように表せる。
$$NDL(d_k)=\frac{DL(d_k)}{\overline{DL}}$$
・コードの説明として、前提として、複数の文書からなる全文書Dがあり、そのうちの一つ(d)をdocとしてこの関数に渡しているとする。__「term_list」はdocをスペースで区切ることで単語に分割しており、「doc_len」はこの単語の個数である。その他の文書についてもfor文で「term_n_list」に単語を格納し、「sum_doc_len」に全文書の長さを格納している。
・計算部分は、公式通りに行えば「(doc_len)/(sum_doc_len/len(D))」であるが、割り算が二箇所で出てきているので、「(doc_len*len(D))/(sum_doc_len)」__としている。
・以上のNDFも含め、計3つの合成指標であるBM25は、以下の特徴がある。
・文書d中にクエリqが頻出であるほど値は大きくなる(TF)
・全文書中でクエリqが頻出であるほど値は小さくなる(IDF)
・文書dが短いほど値は大きくなる。(NDL)
・BM25の具体的な定義は以下のようになる。
$$BM25(q,d)=IDF(q);\frac{(K_1+1);TF(q,d)}{K_1;(1+b;(NDL(d)-1);)+TF(q,d)}$$
・以上の定義について、「$k_1$」は単語の__出現頻度__による影響を、「$b$」は文書の__長さ__による影響を、それぞれ調整するハイパーパラメータである。一般的に、「$k_1$」は1.5、「$b$」は0.5に設定されることが多い。
PageRank
・__PageRank__は、__リンク関係__をもとに__Webページの重要度__を決定するアルゴリズムである。前項までの3つはクエリ依存型であったが、これは__クエリ非依存型__である。
・PageRankの概念は、簡単に言うと「__多くのWebページから__リンクが飛んでいるWebページは重要である」「重要なWebページから__飛んでいるWebページも重要である」となる。
・(発展)PageRankの求め方をにみていく。一つの求め方として「グラフ理論」__があり、各ページをノード、リンクをエッジとみなした行列(隣接行列)を考える。隣接行列Aについて、あるノードiから他のノードjにリンクが伸びているときに1、そうでない時に0をとるとする。また、このAを転置させた場合、逆にノードjからノードiにリンクが飛んでいる時1を取ることになる。この時列について正規化した行列をBとすると、このBは__推定確率行列__と呼ばれるものになる。この成分については、ノードjにいるユーザーがノードiにジャンプする確率を表し、この最大固有値の固有ベクトルの各要素の値が、PageRankとなる。
ランキング学習のアルゴリズム
重みベクトルの学習方法
・前項まで特徴ベクトルについて見てきたが、ランキング関数を求めるには__重みベクトル__も学習する必要がある。ここでは、その手法を紹介する。
・重みベクトルの学習方法としては、「一度に見る文書データの数」に応じて__「ポイントワイズ法」「ペアワイズ法」「リストワイズ法」の3つに分けられる。
・それぞれポイントワイズ法は__1つの文書、ペアワイズ法は__2つの文書__、リストワイズ法は__全ての文書__を直接ランキングにして学習を進める。
今回は、このうちポイントワイズ法である__「2値分類」「PRank」と、ペアワイズ法である「Pairwise」__を学んでいく。これらは全て__パーセプトロン__と言うアルゴリズムを使って重みベクトルを学習させる。これは、データ1つ1つに対して学習と予測を繰り返し、予測を間違えた場合に重みベクトルを更新する__と言うものである。
・パーセプトロンは__逐次学習、すなわちデータ更新の際に既存データを再計算する必要のない学習法であるので、他の手法との親和性が高い。
・__2値分類__は、特徴ベクトルとそのラベルを教師データとして、ラベル(適合or不適合)を予測できる重みベクトルを得る学習である。
・PRankは__m個の離散値(0,1,2...m-1)__で与えられたラベルを予測するもので、2値分類と同じ重みベクトルの計算に加え、m+1個の__閾値__により、ランキング関数の値をラベルの値ごとに分類し予測する作業も行う。
・__Pairwise__は2組の特徴ベクトルについて、そのリストと、そのラベルについて学習する手法である。このうち、ラベルの値が大きい方を予測する。
・上記3つの手法では、Pairwiseが最も精度が高くなる。
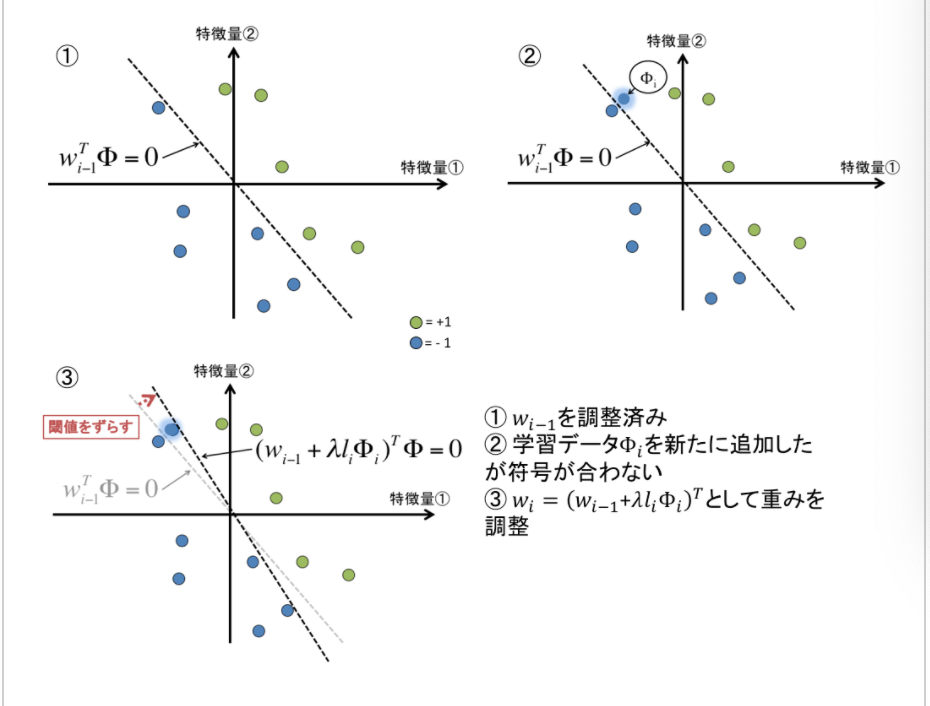
二値分類
・ランキング学習の__二値分類__とは、与えられたクエリ-文書ペアの特徴ベクトルから、__「適切(+1)」「不適切(-1)」__の二種類のラベルを予測する分類作業である。具体的には、パーセプトロンを使って重みベクトルの更新を行う。
・定義について、学習データは、n個のクエリ文書ペアに対してn個の特徴ベクトル(k次元)$\Phi_i$、正解ラベル$l_i$が与えられる。また、k次元の重みベクトルの初期値$w_0$は、0がk個のベクトルであるとする。
・流れについて、まず0個目の特徴ベクトル$\Phi_0$と重みベクトル$w^T_0$との内積を取り、予測ラベル$l'_0$を算出する。この$l'_0$が、正解ラベル$l_0$を予測できていたら、すなわち2つの符号が同じなら、重みベクトルはそのまま、次の次元に移行する。2つの符号が異なる場合は、重みベクトルに$\lambda l_0\Phi_0$を加えて更新する。この時の$\lambda$は__学習率__で、教師データのモデルに反映させる強さを表す。更新したら、同じように次の次元に移行する。イメージは以下の通り。
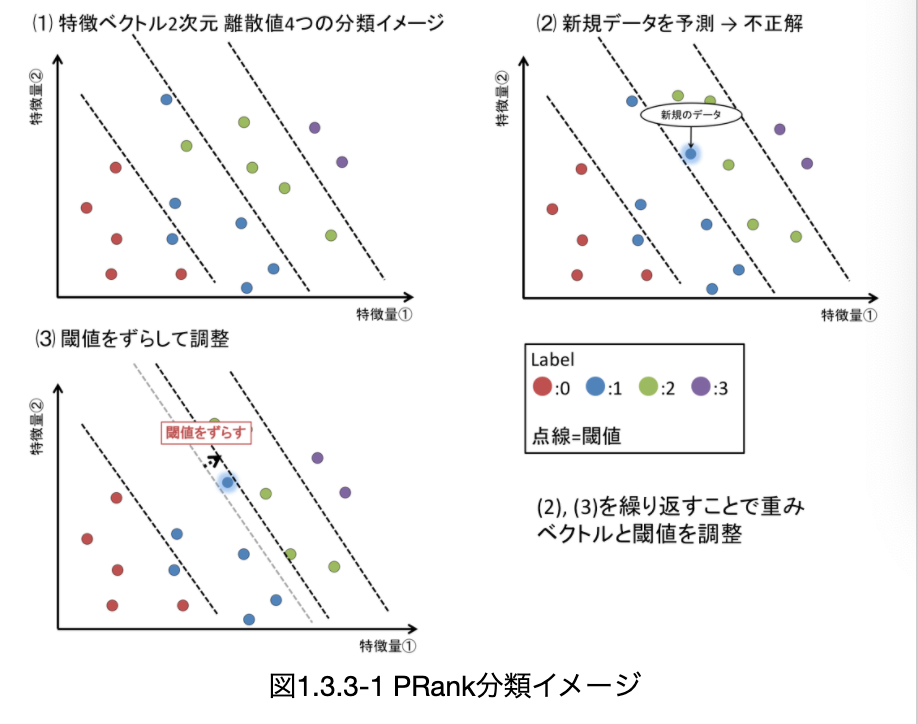
PRank
・__PRank__は、与えられたクエリ文書ペアのラベルを複数の閾値により分類するアルゴリズムである。この手法におけるラベルはm個の離散値(0,1,2...,m-1)となる。イメージは以下の通り。
・PRankの基本的な流れは二値分類と同じである。学習データは、n個のクエリ文書ペアに対してn個の特徴ベクトル(k次元)$\Phi_i$、正解ラベル$l_i$が与えられる。
・モデル内の変数として、k次元の重みベクトル$w_i$とm個の閾値$b_j$を用意する。
・まずは0個目の特徴ベクトル$\phi_0$と重みベクトル$w^T_0$との内積を取る。これを超える__最小__のラベル値$l'0$を予測ラベルとする。そして、予測ラベルと正解ラベルが一致していた場合は重みベクトルと閾値ベクトルは更新しない。
・一致しない場合は重みベクトルと閾値ベクトルを更新する。この時、変更のためのベクトル$\tau^r_0$を用意する。これはrの値が_「予測ラベル以上正解ラベル未満」の時__1、「正解ラベル以上予測ラベル未満」の時-1、それ以外で0とするベクトルである。これを使った更新式は以下の通り。
Pairwise
・__Pairwise__は、クエリが同じでラベルの異なる__クエリ文書ペア$A(q,d_a),B(q,d_b)$について、AとBのどちらの重要性の方が高いかを分類する手法である。
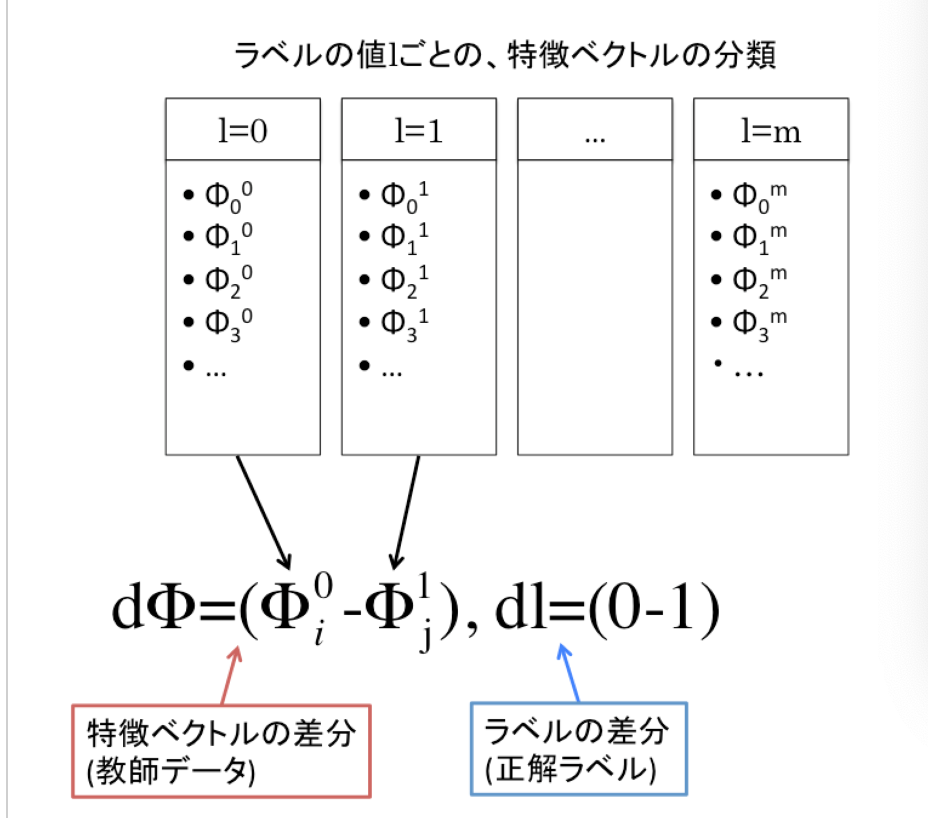
・基本的な流れは__二値分類と同じ。学習データはn個のクエリ文書ペアに対してn個の特徴ベクトル(k次元)$\Phi_i$、正解ラベル$l_i$が与えられる。ただし、このままではPairwiseでは学習できないため、__特徴ベクトルとラベルをそれぞれペアにして差分を取る__と言うことを行う。
・具体的には、正解ラベルlごとにまとめられたリストから、ラベルlが異なるモノ同士でペアを作り、特徴ベクトルの差分「$d\Phi=(\Phi_i^{m_1}-\Phi_j^{m_2})$」と、ラベルの差分「$dl=(l^{m_1}-l^{m_2})$」をそれぞれ訓練データ、正解ラベルとする。図は以下を参照。
・Pairwiseでは、この$d\Phi$が与えられた時の$dl$の符号が予測できる重みwを学習していく。学習方法は二値分類と全く同じ。
性能評価の指標
・ランキングの適切さを図るための指標としては、以下のようなものがある。
・Precision@K
・Average Precision
・Reciprocial Rank
・DCG, NDCG
・また、ランキング学習の性能評価では、__「ランキング上位の正確さ」__が重視される。
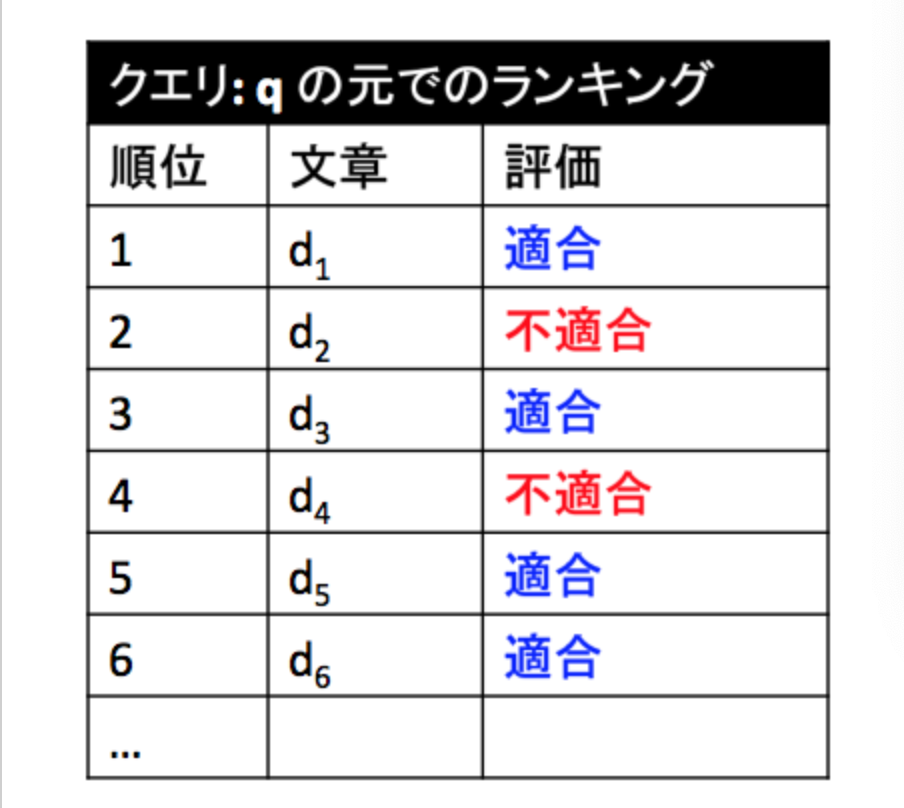
以降では、下図のように、文書に順位とラベルが与えられたものをランキングとして定義している。
Precision@K
・__Precision@K__は、ランキングの上位K番目までの文書のうち、__適合であるものの割合__をスコアとするものである。前項の図でK=6、すなわち上位6文書の適合率を見ると、4/6=「2/3」であることがわかる。
Average Precision
・__Average Precision(AP)__について、ランキングk位までを対象にしたAP(k)は、それより上位のランキングで適合である文書$d_i$について、__Presicion@iの平均をとったもの__である。例えば上図でAP(3)であれば、3位より上位で「適合」であるのは「1位」「3位」であるので、Precision@1とPrecision@3を算出し、その平均を取れば良い。計算すると、(1+2/3)/2=「5/6」がAP(3)である。
・このように算出されると、__ランキング上位の適合文書は重複して計算される__ことになるので、その分ランキング上位の適合度が重要視された手法であるといえる。
Reciprocial Rank
・__Reciprocial Rank(RR)__は、最初に適合文書が出てくる順位がK位__である場合、「1/K」__で算出される指標である。例えば、1位と2位が不適合で、3位が適合であった場合、K=3であるので、RR=「1/3」と言うことになる。
・ユーザーごとにRRの平均をとったものを__MeanReciprocialRank__という。実際にはこちらが使われる。
DCG, NDCG
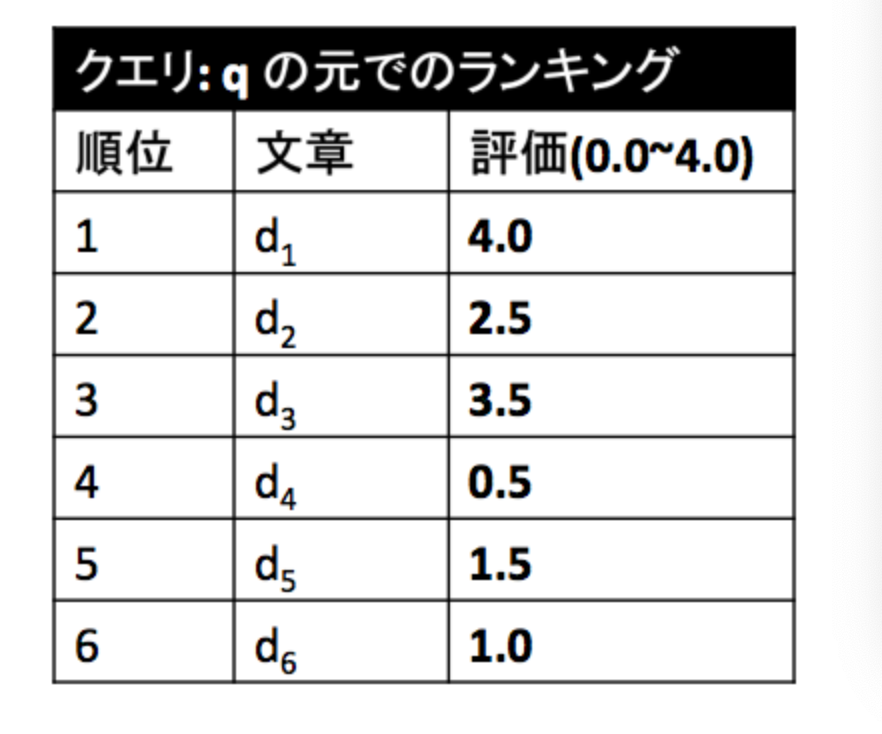
・__DCG__はDiscounted Cumulative Gainの略で、順位によって__割引されたスコア__の合計値を表す。DCGで扱うランキングは、評価が「適合」「不適合」ではなく、数値で与えられた、以下のようなものである。
・割引の仕方について、ランキング2位以下の評価$r_k$について、これを$log_2r_k$で割ることで行う。
・__NDCG__はDCGを__正規化(Normalized)した指標であり、上記手法で算出したDCGを「ランキング内の全ての評価が満点である場合」__のDCGで割ることで算出される。(上記図で言うと、満点は4.0)
まとめ
・ランキング学習__とは、定義した重要度に基づいて__情報を並べる__ための機械学習の手法である。この学習を行う際の指標となるのが__ランキング関数__で、一般的には「特徴ベクトルと重みベクトルの内積」で求められる。
・特徴ベクトルの成分には「TF」「IDF」「BM25」「PageRank」がある。
・重みベクトルの学習方法としては「二値分類」「PRank」「Pairwise」__がある。
・ランキング学習の性能評価指標としては、「Precision@K」「Average Precision」「Reciprocial Rank」「DCG,NDCG」がある。
今回は以上です。最後まで読んでいただき、ありがとうございました。