Aidemy 2020/12/8
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、ネットワーク分析の2つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・karate clubについて
・中心性について
・グラフの分割
ネットワーク分析の実践
karate club
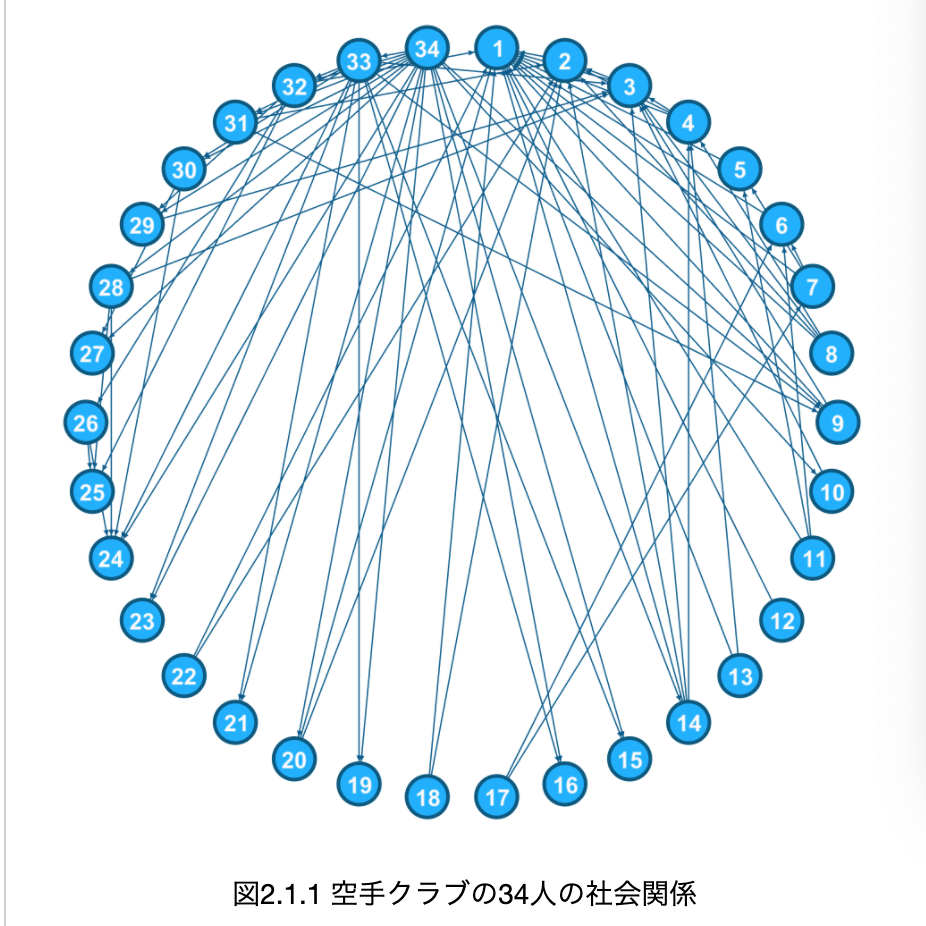
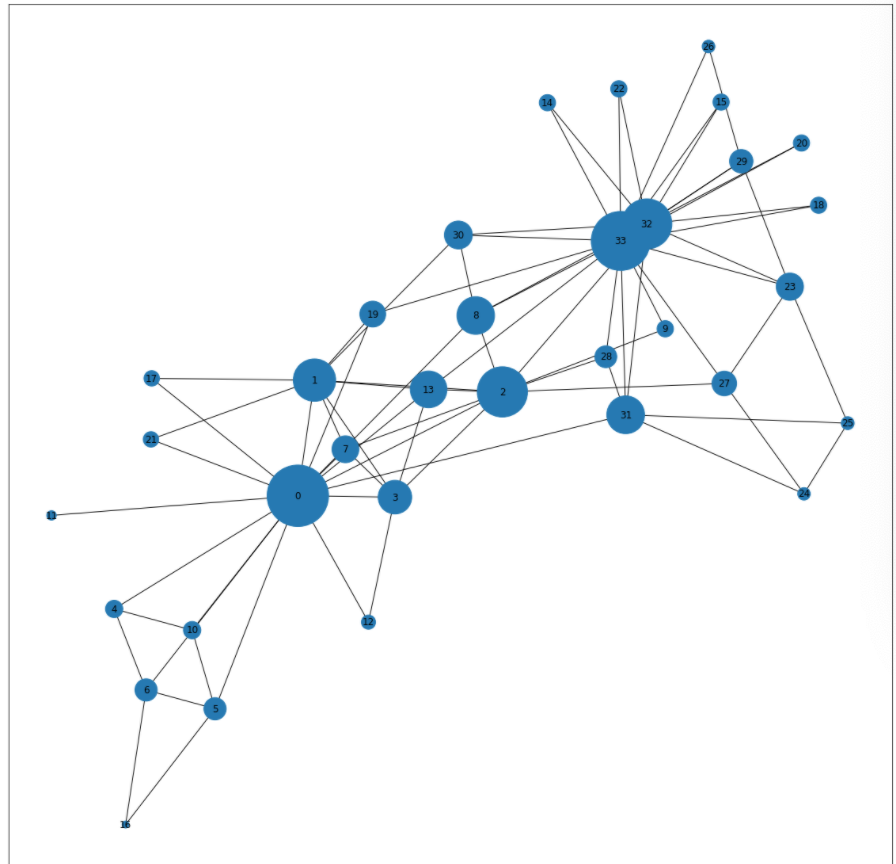
・このデータセットは、米国のある大学の__空手クラブの交友関係__を示したものである。これを使って、__中心人物の特定__や__コミュニティの抽出__などの様々なネットワーク分析が行える。
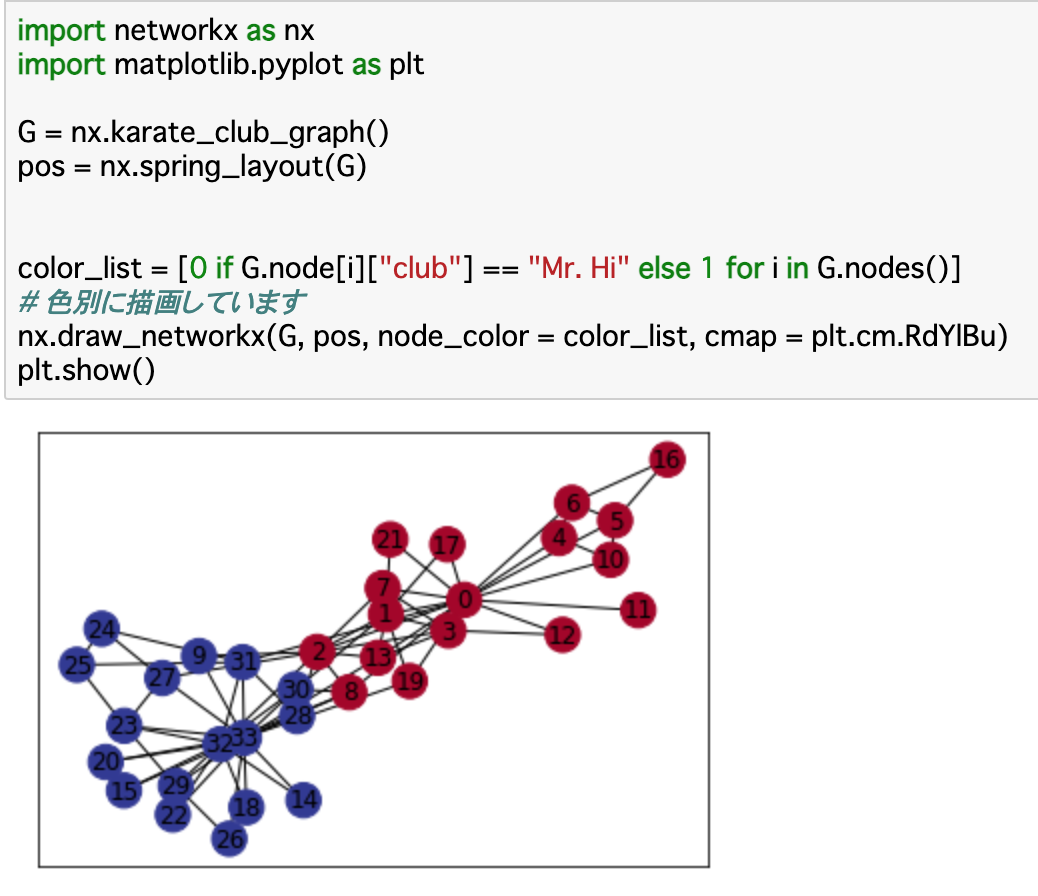
・Chapter1で扱った__networkx__では、__「nx_karate_club_graph()」とするだけで、このデータセットを呼び出すことができる。また、この描画も今までにやった方法で行える。
・また、この頂点は「属性」を有している。ここでいう属性は、大学の__2つのクラブ(club)を表している。例えば「G.node[18]['club']」とすると「Officer」と__出力され、他の頂点についてもみると「Mr. Hi」__と出力されるものもある。以下のコードでは、この2つの属性ごとに頂点を色分けしたものである。
中心人物を見つける
・直感的な理解の通り、グラフの辺は、頂点同士に繋がりがある__ことを示す。社会ネットワークの例で言えば、人間関係のグラフにおいて、各頂点がその組織を構成する人間であるとすると、頂点AとBを結ぶ辺は、AさんとBさんの間に何らかのつながりがあることを示す。
・各頂点がネットワークの__構造上どれぐらい有利な状態であると言えるか__という指標を数値化したものが「中心性」__である。人間関係の例で言えば、__より多くの人と繋がりを持った方が有利__であるといえ、また、多くのつながりを持った人と繋がることも有利__であると言える。
・中心性の一つとして、「固有ベクトル中心性」がある。グラフGにおける固有中心性は「nx.eigenvector_centrality_numpy(G)」__で取得できる。この値が大きいほど重要度が高いということになる。以下では、karate clubにおける固有ベクトル中心性を算出している。
媒介中心性
・ここでは、固有ベクトル中心性とは別の中心性を見ていく。また、ここでいう__「経路」__は全て最短経路を示すこととする。
・人間関係の例で、AさんとBさんは直接のつながりはないが、他の人物を経由することで__つながりが見出せる場合を考える。すなわち、頂点AからBへの経路が存在する場合である。この場合、経路上に存在する頂点は、AさんからBさんへの__情報伝達の役割を担っている__といえ、この「情報伝達の役割を持った頂点」を有利な状態と考えて定義された中心性が「媒介中心性」と呼ばれるものである。この値が高いほど、より多くの情報伝達の役割を担っていると言える。
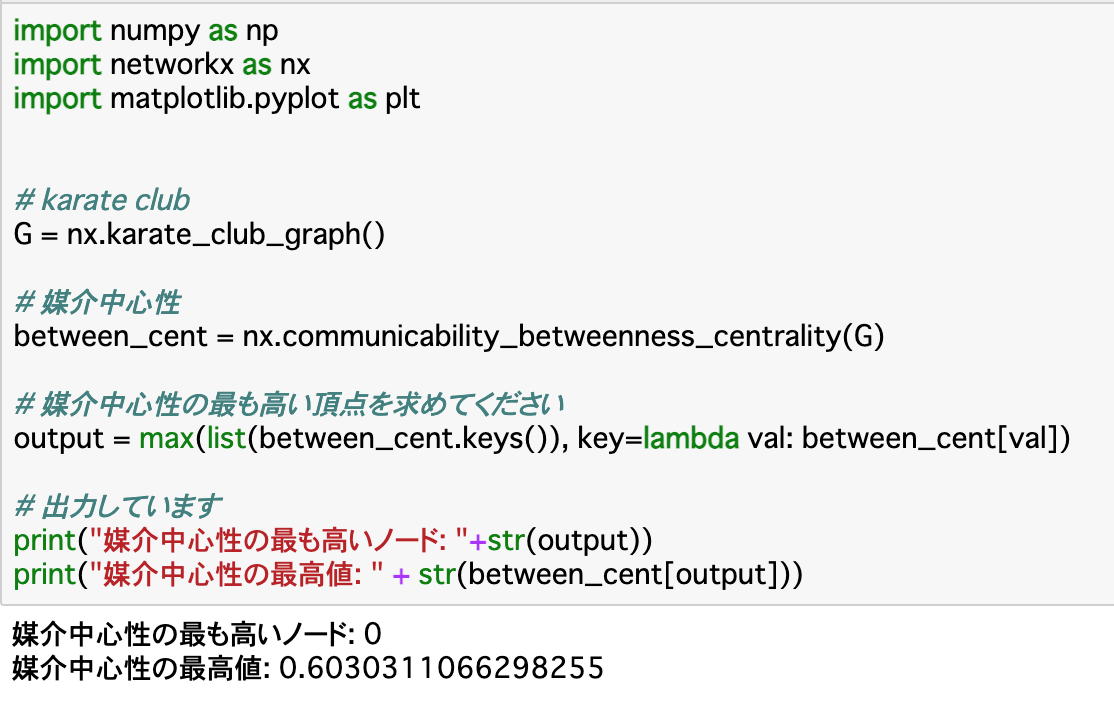
・グラフGにおける媒介中心性は「nx.communicability_betweenness_centrality(G)」__で求められる。
最も中心性が高い頂点を求める
・karate clubで__最も中心性の高い頂点を求める__。求め方は、固有ベクトル中心性、あるいは媒介中心性をリストと見て、その中の__最大値を取れば良い__。具体的には、以下の通り。
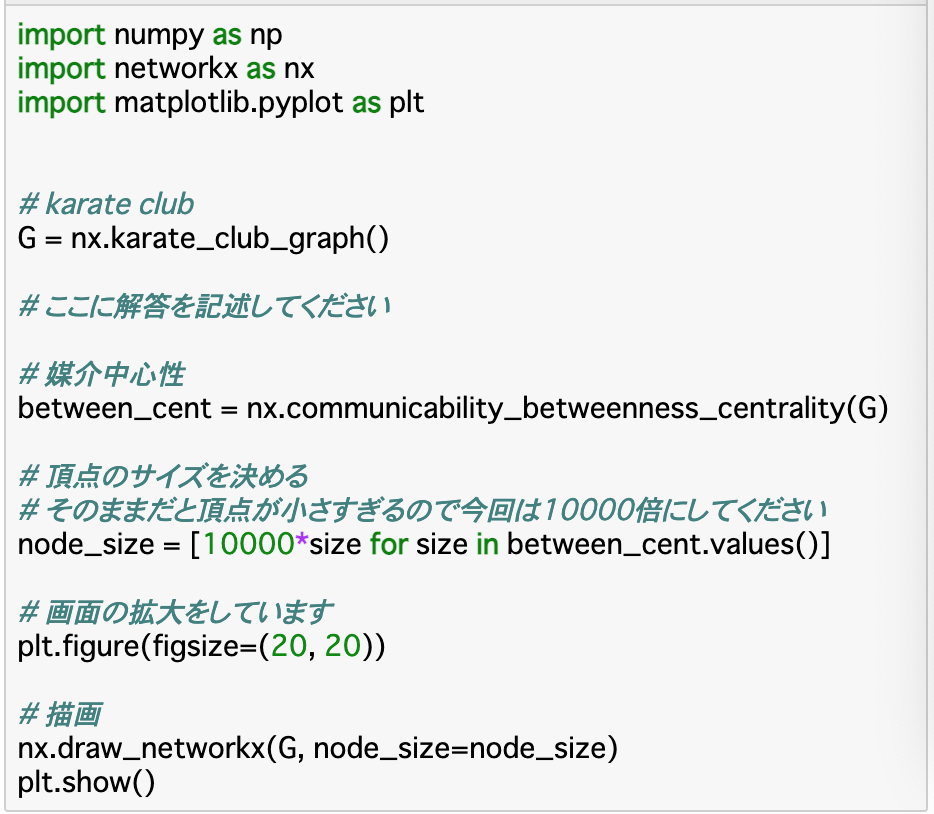
中心性の大きさに応じて頂点の大きさも変える
・頂点の大きさ__を、中心性の大きさに応じて大きくするということを行う。頂点の大きさは、「nx.draw_networkx()」の引数で「node_size」__を指定することで変更できる。以下では、それぞれの頂点の媒介中心性の値(size)に10000をかけることで、そのままnode_sizeとしている。
グラフの分割
連結成分
・グラフをいくつかのグループに分ける__ことを考える。この時のそれぞれのグループのことを「サブグループ」という。このようにグラフが分割される時、サブグループを__連結成分__ともいう。「nx.connected_component_subgraphs(G)」__とすることで、それぞれの連結成分が返される。
クリーク
・前項でおこなったグラフの分割は、連結成分があることが前提であったため、これがない場合、すなわち__全結合グラフ__である時は、グラフの__密度__に注目して分割していく。頂点の個数をn、辺の個数をmとすると、有向グラフの時は$\frac{m}{n(n-1)}$、無向グラフの時は$\frac{2m}{n(n-1)}$で算出することができる。
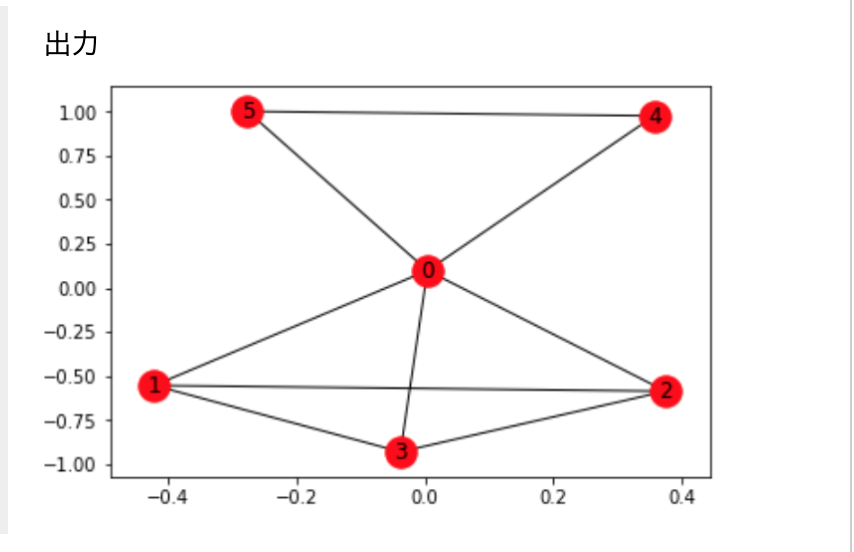
・__頂点が3つ以上__あり、かつ__密度が1(最大)であるサブグラフのことを「クリーク」__という。以下のグラフは、頂点が3つ以上あり、全ての頂点が、他の全ての頂点と辺で繋がっているので、クリークであると言える。
・また、以下では、グラフGと、そのグラフの任意の3つの頂点のリストを引数とし、その3つの点がクリークを形成するかを判定する関数__「is_clique()」である。
・まずは3つの頂点をそれぞれペアにして、リストに格納する。渡された3点のうち2つをiとjとし、それぞれ同じものでなければ(i,j)としてnode_pair_listに格納する。
・そらにこのそれぞれのペアについて、(頂点A,頂点B)あるいは(頂点B,頂点A)のどちらかのペアが、グラフの辺「G.edges()」の中にあれば、「AとBは繋がっている」__ということができ、全てのペアについて「繋がっている」判定がなされた時は、クリークが形成されるとしてTrueを返す。
n-クリーク
・前項でクリークについて学んだが、実際のグラフでクリークが形成されることはあまりない。クリークの条件は、言い換えれば__「サブグラフに含まれる全ての頂点間の距離」が「1」であるもの__を指すので、この条件を緩くして、__「距離の最大値がn以下である」ものを「n-クリーク」と呼ぶ。
・以下は、頂点のリストと「n」、最短距離が与えられた時、与えられた頂点がn-クリークを形成するかを判定する関数「is_n_clique()」__である。判定するには、__距離の最大値__を求めれば良いので、各頂点i,jについての距離__dist[i][j]の最大値がn以下__だったらTrueを返すようにすれば良い。
クラスタリング
・ネットワーク分析における__クラスタリング__は、グラフ理論を用いた分析手法を指す。具体的には、連結されたグラフを__いくつかのサブグラフに分割する操作のこと__を__クラスタリング__という。また、この時のサブグラフを__コミュニティ__という。
・ネットワークにおけるクラスタリングのメリットとして、大規模なネットワーク構造でも、__自動でノードの分類ができる__ことが挙げられる。また、具体的な活用例として、SNSの個々のアカウントをノード(頂点)としてクラスタリングを行うことで、個人に最も適した広告やレコメンドなどを行うことが可能になる。
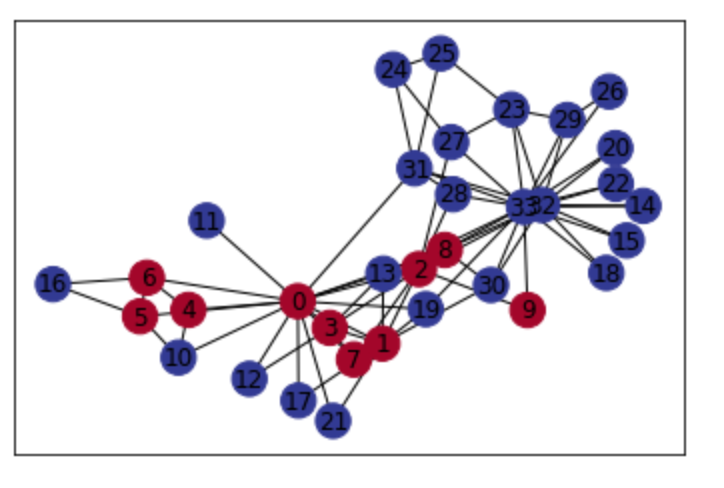
・networkxでは、__community__モジュールの__best_partition()__を利用することでクラスタリングが行える。以下ではそれを実行している。各ノードと、何番目のコミュニティに属するかが辞書型で渡されている。
コミュニティごとに色分けする
・前項で算出した__「partition」__の値は、属するコミュニティ__を示すので、partitionの値が同じもの同士で色分けすることで、属するコミュニティをわかりやすく可視化する。以下ではこれをおこなっているが、各色について、引数の「cmap」では「plt.cm.RdYlBu」__で指定している。これは、__ランダムに色を変化させるもの__で、振り分けられる色は__発散的__になっている。今回は頂点番号が1桁のものと2桁のもので色分けしている。その場合、__node_color__には__これを満たす条件式__を指定する。
モジュラリティ指標
・ここでは、__「良い分割」__を評価する手法を紹介する。「良い分割」とは、各コミュニティ内の結びつきが強く、コミュニティ同士の結びつきは弱い__ものとなるような分割である。この指標となるのが「モジュラリティ指標」である。これは「community.modularity(partition,G)」__で求められる。この値が高いほど良い分割であると言える。
・以下では、ここまでの分割手法「community.best_partitionによる分割」と「頂点番号による分割」のモジュラリティ指標を算出している。
まとめ
・データセット__「karateclub」を呼び出すには「nx.karate_club_graph()」とすれば良い。
・ネットワーク上で頂点がどれくらい有利であるかを示すのが__中心性__である。人間関係では、より多くのつながりを持っていたり、つながりを持った人とつながることで中心性が高いとみなされる。中心性は「固有ベクトル中心性」「媒介中心性」__がある。
・グラフをいくつかのグループに分けるとき、分けられたそれぞれのグループを__サブグループ(連結成分)という。また、全ての頂点がつながっているサブグラフを__クリーク__という。また、このサブグラフに分割することを__クラスタリング__ということもあり、この時のサブグラフを__コミュニティ__という。また、このコミュニティの分割を評価する指標となるのが「モジュラリティ指標」__である。