Aidemy 2020/10/29
#はじめに
こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
今回は、次系列分析の4つ目の投稿になります。どうぞよろしくお願いします。
＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・SARIMAモデルの構築
#SARIMAモデルについて
・__SARIMAモデル__とは、データを階差系列に変換するARIMA(p,d,q)を、更に__季節周期を持つ時系列にも対応できる__ようにしたモデルのことである。
・SARIMAモデルでは、__SARIMA(sp,sd,sq,s)__というパラメータを持つ。
##sp,sd,sq
・sp,sd,sq__はそれぞれ「季節性自己相関」「季節性導出」「季節性移動平均」といい、ARIMAのp,d,qと基本的には変わらない。
・sp,sd,sqのデータは過去の季節期間を経たデータに影響されるということが加わった。
・SARIMAのもう一つのパラメータである「s」__は__季節周期__を表す。12ヶ月周期なら、s=12とすれば良い。
・sqに関しては、影響される「過去の季節期間」が何周期前のものかを表す。
##パラメータの決定
・以上のようなパラメータについて、適切な値を調べる必要がある。
・このときに使われるのが、情報量基準__というものである。今回はその中でも「BIC」__というものを使う。ただし、今回は詳しくは扱わない。
・BICの値が低ければ低いほどパラメータの値は適切であると言える。
##自己相関係数/偏自己相関係数の可視化
・__偏自己相関__とは、自己相関を行う二つの値の__間のデータの影響を取り除いたもの__である。
・例えば、y1とy7の偏自己相関は、その間のy2〜y6の影響を除去したものになる。
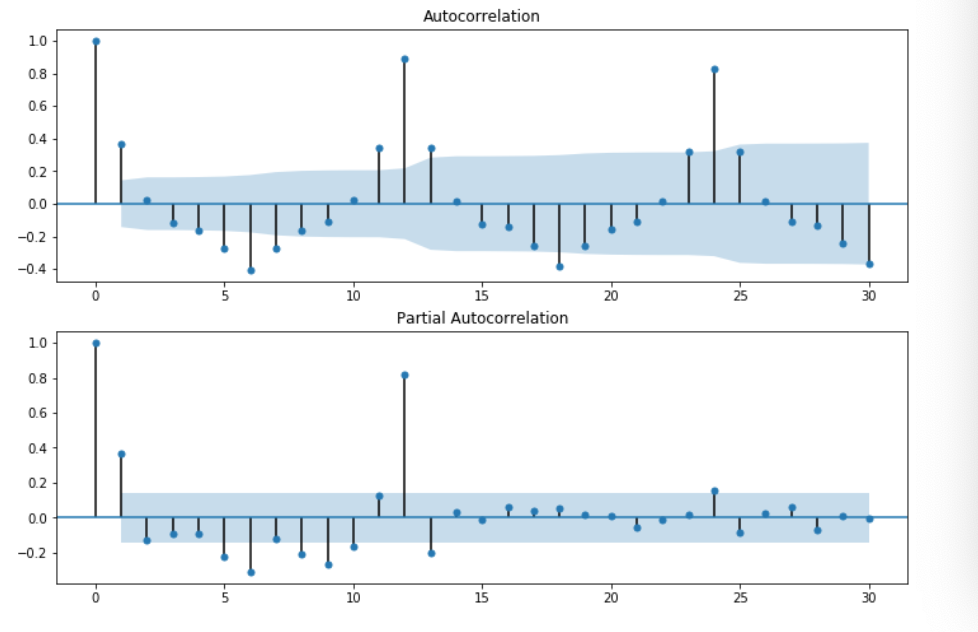
・この偏自己相関を可視化することによって、パラメータ「s」の最適な値を設定する。
・可視化したとき、__周期の部分で偏自己相関の値が高くなる__ので、ここをsの値にすれば良い。
・偏自己相関の可視化（グラフ化）は以下のように行う。
sm.graphics.tsa.plot_pacf(データ)
・コード（ワインの売り上げデータの相関の可視化）
・結果
#SARIMAモデルの構築
・構築の手順
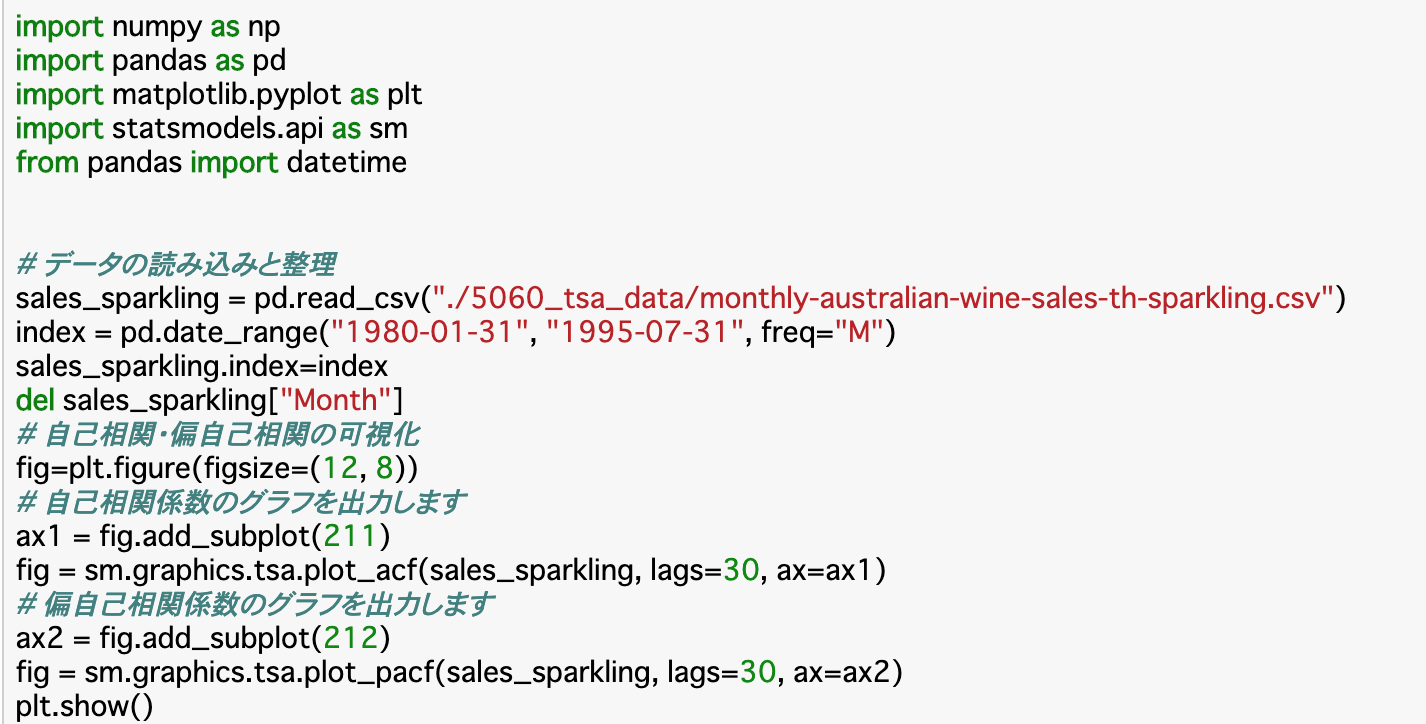
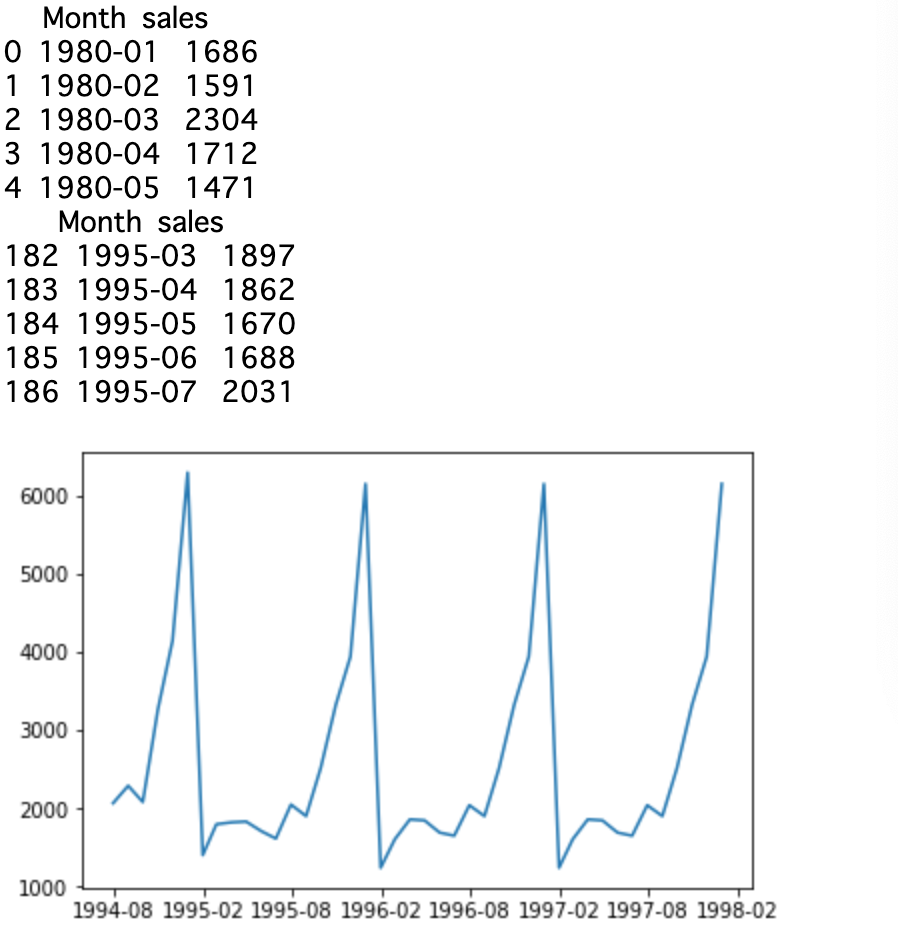
①__データ読み込み__:pd.read_csv()
②__データ整理__:pd.date_range()
③__データ可視化__:sm.graphics.tsa.plot_pacf()
④__データ周期（s）把握__:④から。
⑤__s以外のパラメータ設定__:BICで把握
--ここから新しい部分--
⑥__モデル構築__:sm.tsa.statespace.SARIMAX().fit()
⑦__データ予測/可視化__:predict() / plt.show()
・⑥モデル構築のSARIMAX()の引数については以下のようになる。
SARIMAX(データ,order=(p,d,q),seasonal_order=(sp,sd,sq,s))
・⑦データ予測のpredict()は以下のようになる。予測開始時だけは時系列データにある時間である必要がある。
モデル.predict("予測開始時","予測終了時")
・一連のコード実行（⑤は行っていない）
・結果
#まとめ
・SARIMAモデル__とは、データを階差系列に変換するARIMA(p,d,q)を、更に季節周期を持つ時系列にも対応できるようにしたモデルのことである。
・SARIMAモデルにはパラメータ(sp,sd,sq,s)__がある。
・sp,sd,sqは__BIC__という__情報量基準__を用いて適切な値を調べる。
・sは__偏自己相関__を図式化して調べる。
・これらのパラメータを__sm.tsa.statespace.SARIMAX().fit()__に渡してモデルを構築し、__predict()__で予測を行う。
今回は以上です。最後まで読んでいただき、ありがとうございました。