Aidemy　2020/10/

はじめに

　こんにちは、んがょぺです！バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます！
　今回は、次系列分析の1つ目の投稿になります。どうぞよろしくお願いします。

＊本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。

今回学ぶこと
・時系列分析について
・時系列データの種類
・時系列データの統計量

時系列分析について

時系列データとは

・時系列データとは、時間と共に値が変化するデータのことを指す。例えば、時間ごとの気温や売上高、株価などが当てはまる。
・特に、商品の売り上げ予測、来店者数の予測など、ビジネスにおいて重要な分析である。
・時系列分析は、pythonのStatsModelsを使って実装する。

（復習）時系列データの表示

・時系列分析には、時系列データをグラフで図式化することが不可欠である。図式化にはMatplotlibを使う。以下で、今回出てくるpltの復習をする。

・グラフの作成:plt.plot(x,y)
・グラフの表示:plt.show()
・x軸の表示範囲を設定:plt.xlim([,])　（y軸ならylim）
・グラフのタイトル:plt.title("")
・x軸のタイトル:plt.xlabel("")　（y軸ならylabel）

時系列データのパターン

・時系列データには以下の3パターンがある。時系列データは、これら3パターンが組み合わさってできている。
　・トレンド:長期的なデータの傾向。値が上昇していれば「正のトレンド」、減少していれば「負のトレンド」という。
　・周期変動:時間経過に伴ってデータの値が上昇と下降を繰り返すこと。特に1年間の周期変動を季節変動という。
　・不規則変動:時間経過にかかわらず、データの値が変動すること。

モデリング

・モデリングとは、時系列データを定式化（モデルを構築）することである。
・このモデルを使って予測を行ったりデータ同士の関連を分析したりすることが時系列分析にあたる。

時系列データの種類

・時系列データには、まず加工前のデータそのものである「原系列」がある。この原系列の性質を分析することが時系列分析の目的であるが、実際に分析するのは加工後のデータであることがほとんどである。
・加工後のデータには、「対数系列」「階差系列」「季節調整済み系列」などがある。以下ではそれぞれについて詳しく見ていく。

対数系列

・時系列データのうち値の変動が大きいデータについて、その変化を穏やかなものにすることを対数変換と言い、対数変換を行ったデータのことを対数系列という。

・対数変換を行うには、以下を実行すれば良い。
np.log(DataFrameのデータ)

階差系列

・時系列データのうち、一つ前の値との差をとって扱うことを階差系列という。
・階差系列に変換すると、トレンド（長期的な傾向）を取り除くことができる。
・トレンドを取り除くことで「時間経過にかかわらず全体を見ると時系列の値が変化しない」ということを示す定常過程にすることが可能になることがある。定常過程については後述する。

・階差系列を行うには、以下を実行すれば良い。
DataFrameのデータ.diff()

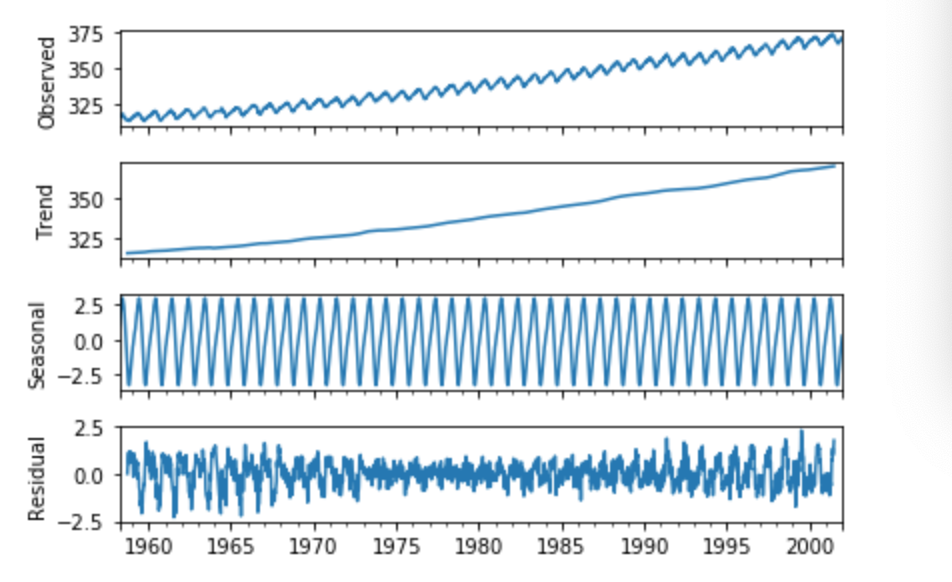
季節調整済み系列

・1年間の周期変動のことを季節変動といったが、季節変動のあるデータは、そのままでは「季節変動パターンではないデータの分析」が難しい。このような場合に対処するため、季節変動を取り除く処理をすることがあり、この加工を行なったデータのことを季節調整済み系列という。

・季節調整済み系列を行うには、以下を実行すれば良い。(smはstatsmodelsのこと)
sm.tsa.seasonal_decompose(データ)

・コード

・結果

時系列データの統計量

期待値（平均）

・各時系列データの平均値を期待値(Expectation)という。
・平均値はnp.mean()で求めることができる。

分散/標準偏差

・各時系列データが期待値からどのぐらいばらけているかを示した値が分散である。
・分散は(各データ - 期待値)^2で求められ、この平方根を標準偏差という。
・株、投資の世界では、標準時偏差がリスク計測の重要な指標になっている。

自己共分散/自己相関係数

・自己共分散とは、同じデータ同士の別の時系列での共分散をさす。
・時系列がkだけ離れている時、k次の自己共分散といい、以下のように求められる。
(各データ - 期待値)(kだけ離れたデータ - 期待値)
・上記の式をkについての関数として見たものを自己共分散関数という。

・この自己共分散を、異なる値との間でも比べられるように変換したものが自己相関係数である。
・自己相関係数は、過去の値とどれぐらい似ているかを表している。
・自己相関係数は以下のように求められる。
自己共分散 / (データの標準偏差)(kだけ離れたデータの標準偏差)_
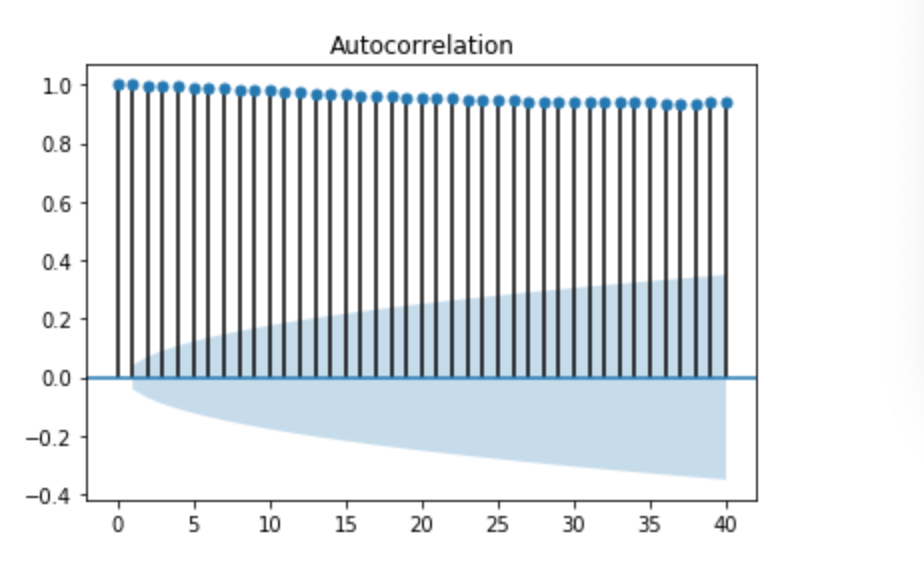
・上記の式をkについての関数として見たものを自己相関関数といい、これをグラフにしたものをコレログラムという。

自己相関関数の出力

・自己相関関数は
sm.tsa.stattools.acf(データ,nlags)で表される。
・グラフ（コレログラム）は
sm.graphics.tsa.plot_acf(データ,lags)で表される。

・引数である「lag」とは「ずらした時系列kの値」のことである。
・相関係数は1.0に近いほど正の相関が強く、-1.0に近いほど負の相関が強いと言える。