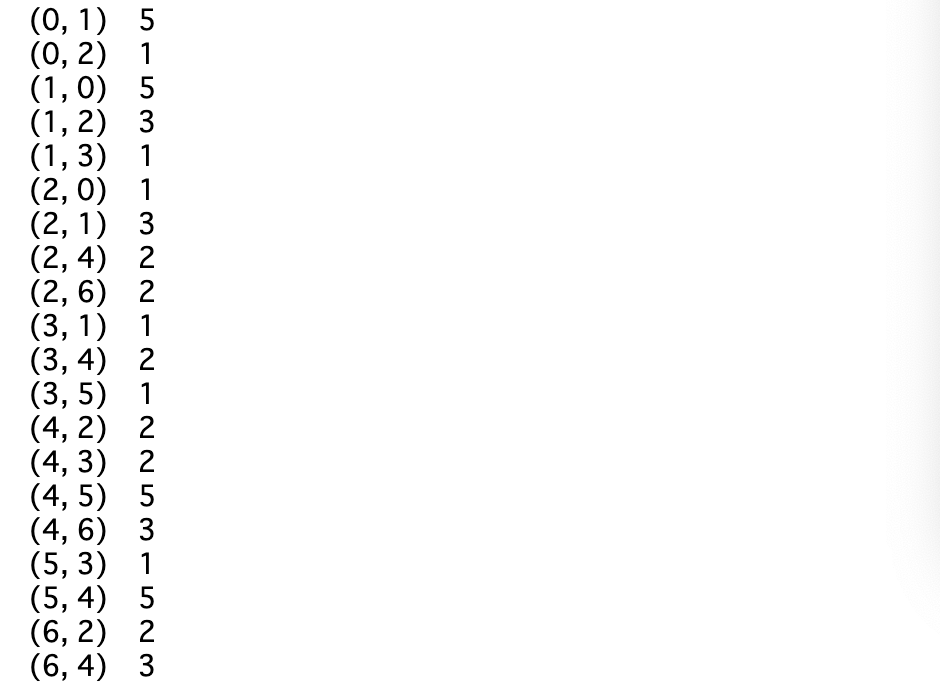Aidemy 2020/12/8
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、ネットワーク分析の一つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・ネットワーク分析について
・基本用語
・グラフの作成
ネットワーク分析について
ネットワーク分析とは
・ネットワーク分析__とは、グラフを用いてさまざまな事象と事象の関係について調べる__という分析手法である。ここでいう「ネットワーク」とは、いわゆるコンピューターネットワークに限らず、広く「複数の点がなんらかの関係で繋がっている(線になっている)」物を指す。例えば、人と人をそれぞれ点とすれば、それを繋げば「人間関係」となる。ちなみに、友人関係、血縁関係といった人間関係は「社会ネットワーク」と呼ばれる。このネットワークを可視化したものが「グラフ」となる。このグラフも、一般的な意味とは必ずしも一致しないため、注意する。
・ネットワーク分析の応用例として、ネットワークの中心性__を分析して影響力のある人物を特定する「ソーシャルネットワーク」、企業間の取引データから業種の分類などを行う「企業間ネットワーク」__などがある。
・今回は、networkx__というネットワーク分析用ライブラリを使い、ネットワークの「クラスタリング」や「中心的なノードの発見法」__を学んでいく。Chapter1では__このライブラリの関数の説明__を行う。Chapter2では__karateclub__というデータセットを使って、実際にデータ分析を行う。
グラフの描画例
・Chapter1では、networkx__ライブラリの使い方の中でも、特に__グラフの記述__についてを学んでいく。グラフは__点と線からなる関係構造を可視化したもの、ということができる。
・グラフの作成はこのnetworkxで行うが、表示については今までと同様に__「plt.show()」__で行う。以下は実際にグラフを作成し、表示したものである。(コードについては後述する。)
グラフ理論の基礎
基本用語
・前項のような、グラフを数学的に扱う分野__を「グラフ理論」という。
・基本用語について、グラフを構成する各点を「頂点(ノード)」という。そして、この頂点同士を結んだ線を「辺(エッジ)」という。
・ベクトルのように「矢印の向き」がある辺を含むグラフのことを「有向グラフ」といい、全ての辺に向きがないグラフを「無向グラフ」という。
・そして、この__点と辺を連続で辿ったもの__を、文字通り「道(path)」__という。有向グラフの場合は、辺の向きが進む方向と一致していなければ、道とはならない。また、一般的に「道」というときは、同じ頂点は二度と通らない物を指す。
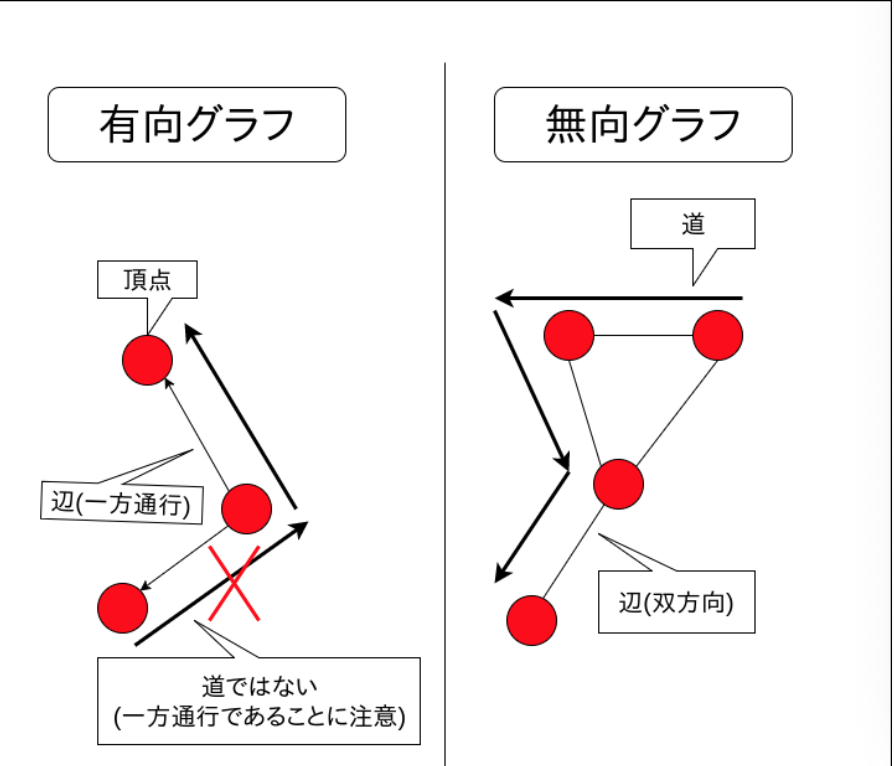
その他の用語(応用)
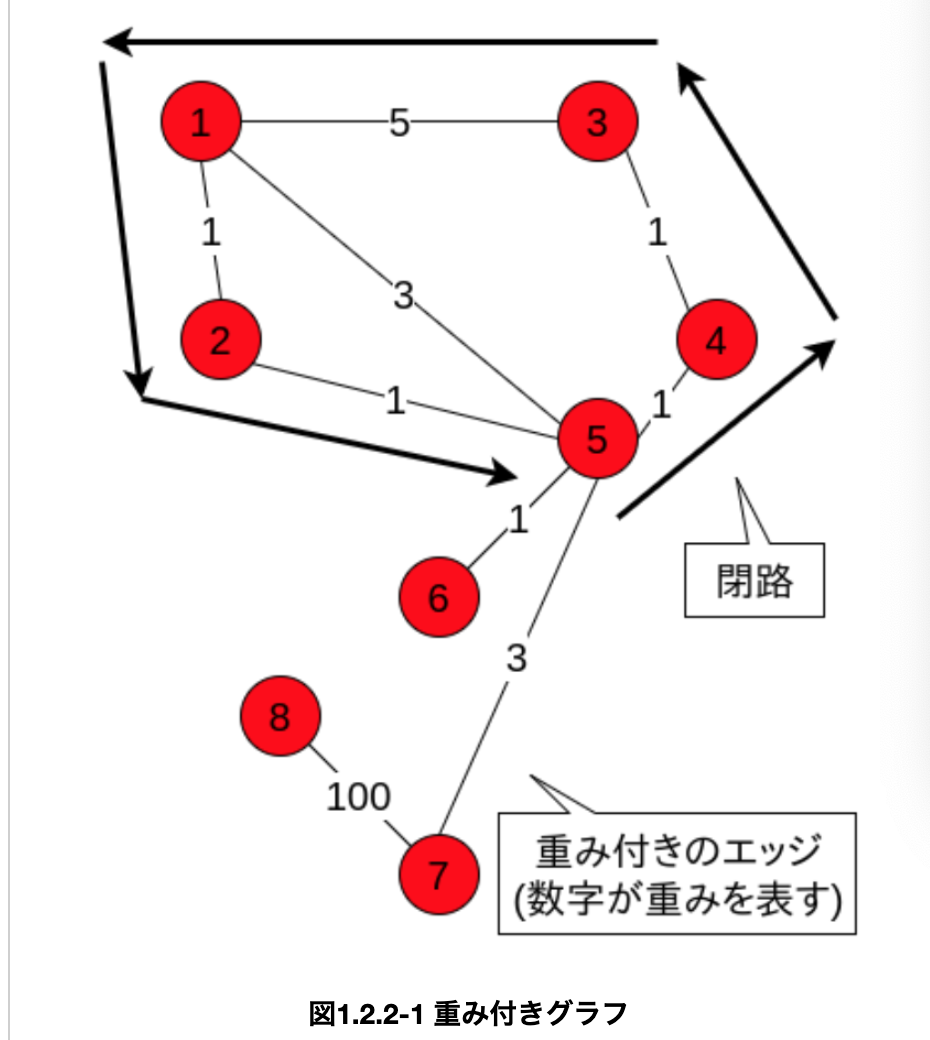
・「辺」に数字が書いてあるものを、__「重み付きグラフ」といい、その数字のことを「重み」という。ニューラルネットワークでよく見られる。また、ある頂点から頂点に移動する道を考えるとき、通過する__重みの合計が最小になるもの__を「最短経路」という。
・道のうち、循環になっている(一回りすると最初の頂点に戻る)物を「閉路」__という。
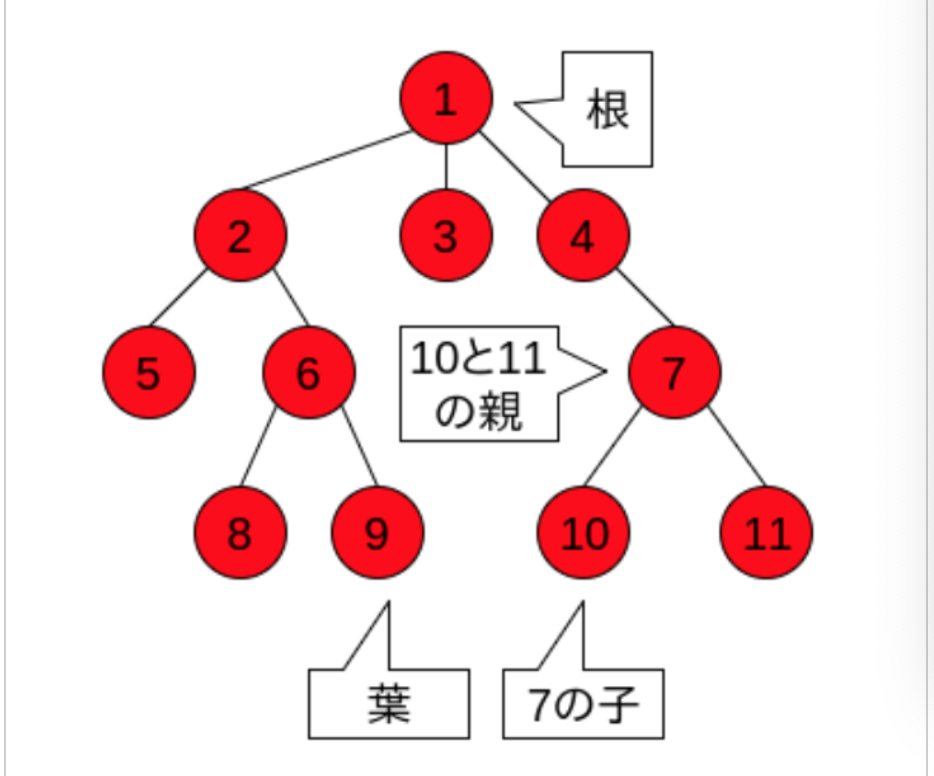
・また、閉路を持たないグラフのことを__「木」という。そして、木の一番上の頂点を「根」、一番下の頂点を「葉」という。自分より上位にある頂点を「親」、下位にある頂点を「子」という。
・木の特徴として、辺の数の合計が「頂点の数-1」__で求められることが挙げられる。
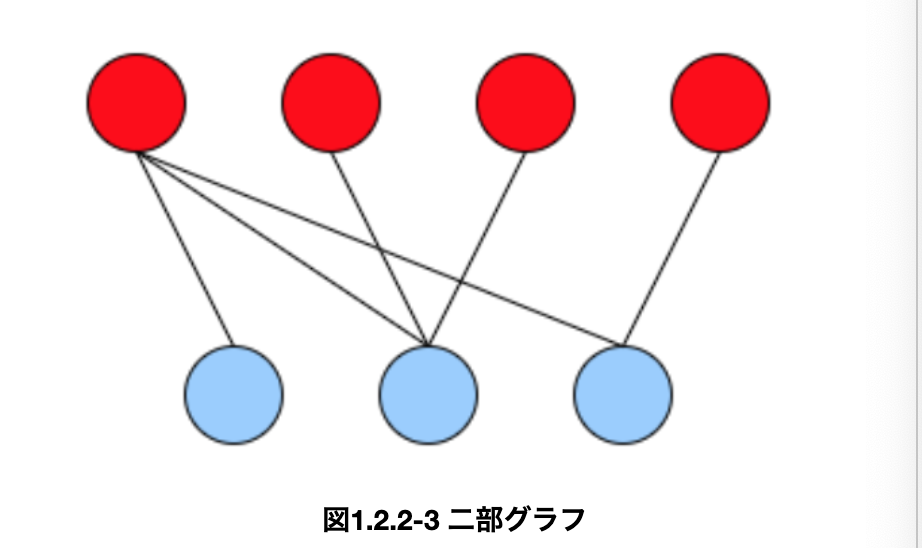
・他のグラフとしては、__「二部グラフ」__というものがある。これは、頂点を__2グループに分け__て、各グループ同士では辺をつくらず、違うグループ同士でのみ辺を作るものを指す。以下の図では、赤いグループと青いグループで分け、同じグループ内では辺が作られていないことがわかる。
用語(発展)
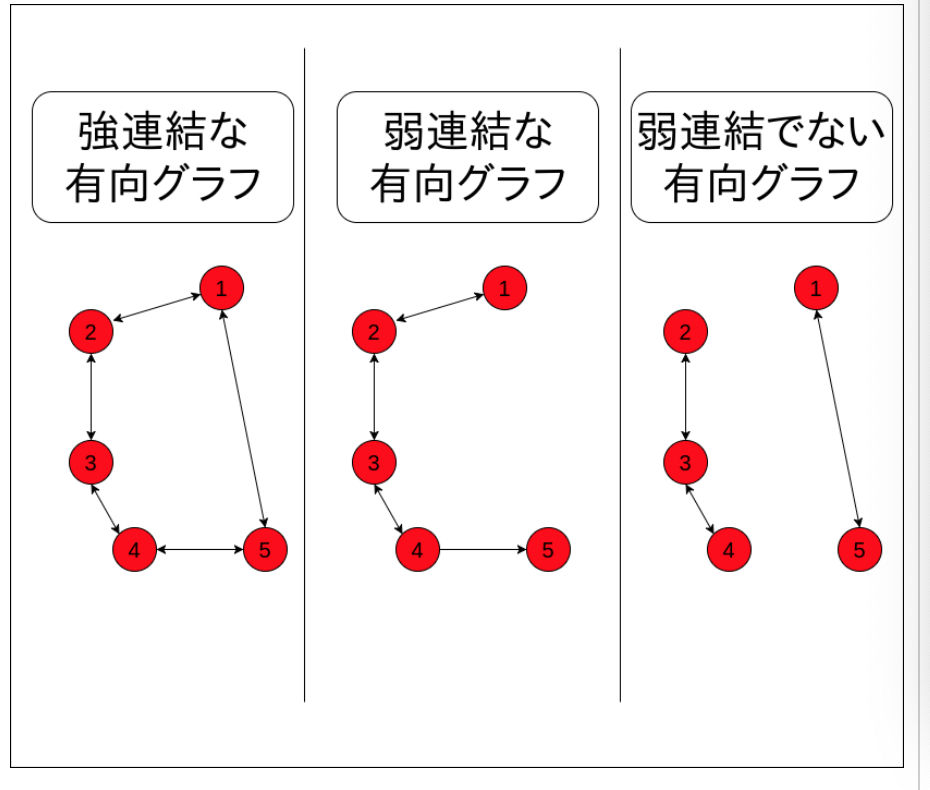
・有向グラフにおいて、方向を無視しないで__どの頂点との間にも道が存在するものを「強連結」という。一方で、方向を無視した場合(無効グラフとして見た場合)に任意の二点間に道が存在するものを「弱連結」__という。
・次に、__隣接行列__について見ていく。以下は、上記グラフのうちの一つ目(強連結の有向グラフ)の隣接行列である。
・それぞれの行についてみてみる。まず一行目については__2列目と5列目が「1」__となっている。これは、__頂点「1」から頂点「2」と「5」への辺が存在している__ことを表す。逆に「0」の部分は頂点1からの辺が存在していないことを表す。また、自分自身(頂点「1」)への辺は存在していないものとして扱う。それ以降の行についても同様に考えることができる。
・そして、以下がこのグラフの__隣接リスト__と呼ばれるものである。
・これは、i番目のリストには、頂点iから辺が出ている頂点が格納されている。基本的には隣接行列から得られる情報と変わりはないが、それぞれ以下のような特徴がある。
・隣接行列の方が計算で扱いやすい。
・隣接リストの方が消費メモリが少ない。
・頂点iからどの頂点への辺が出ているかを確認するとき、隣接リストの方が参照数は少ない。
・最後に、ある頂点につながっている辺の数を__「次数」という。特に有向グラフについて、その頂点に入ってくるような辺の数を「入次数」、出ていくような辺の数を「出次数」__という。
networkxについて
グラフの描画の実装
・以下は、最初に作成したグラフの描画のコード例である。このコードについて、詳しく説明していく。

・まず、「G=nx.path_graph(5)」について、これは「nx.path_graph()」によって「G」という__無向グラフ__を作成していることを示す。引数で、頂点の数を指定する。頂点は後から追加できるので、この値は厳密に決める必要はない。今回の例で言えば、5と指定しているので、それぞれラベルが「0~4」の5つの頂点が一繋ぎの辺となって作成されている。ちなみに、「nx.Graph()」とすることで、まっさらなグラフを作成できる。
・「G.add_edge()」で、指定した頂点を結ぶ__辺を追加__している。この段階で存在していない頂点が指定された場合は__自動的に追加される。
・「pos = nx.spring_layout(G)」__で、Fruchterman-Reingold force-directed algorithmという力学モデルの描画アルゴリズムで、頂点を描画する位置__を決めている。この部分はなくても構わない。
・「nx.draw_networkx(G)」で、作成した__グラフGを描画__する。これを「plt.show()」__とすることで、表示できる。
有向グラフの描画
・有向グラフ__については、グラフの作成時に「nx.DiGraph()」とすれば良い。あとは基本的には同じ。
・有向グラフに限らず、まとめて辺を作成したいときは「G.add_edges_from()」__に、辺のリスト__を渡せば良い。有向グラフの場合、辺の指定は(入力点,出力点)とする。例えば(0,1)なら頂点0から頂点1に向かう辺が作成され、(1,0)なら頂点1から頂点0に向かう辺が作成される。このように__指定順で意味が異なる__ので注意する。
また、頂点をまとめて追加したい時は「G.add_nodes_from()」__に、同じように頂点のリストをまとめれば良い。
頂点と辺の描画
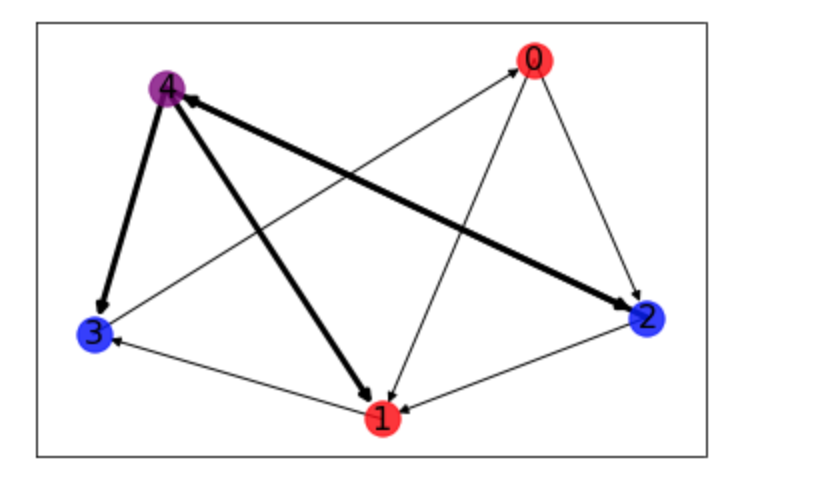
・__「draw_networkx_nodes()」で頂点を、「draw_networkx_edges()」で辺を、それぞれ__色や大きさを指定して__描画することができる。
・各引数について、「G」「pos」はこれまでと同様に指定する。ちなみに、ここでの__posは必須__となる。
・「nodelist」で、描画したい頂点をリストで渡して指定する。「node_color」で頂点の色を指定でき、「node_size」で大きさを指定できる。この3つについては「node」の部分を「edge」とすれば辺についても同じように指定できる。
・頂点について、「alpha」で透過度を指定できる。0〜1の値を取る。また、辺については「width」__で太さを指定できる。
グラフに重みを加える
・グラフGに、__「add_weighted_edges_from()」__というメソッドを使うと、重みを付け加える__ことができる。引数には「(頂点1,頂点2,重み)」__をまとめたリストを渡す。
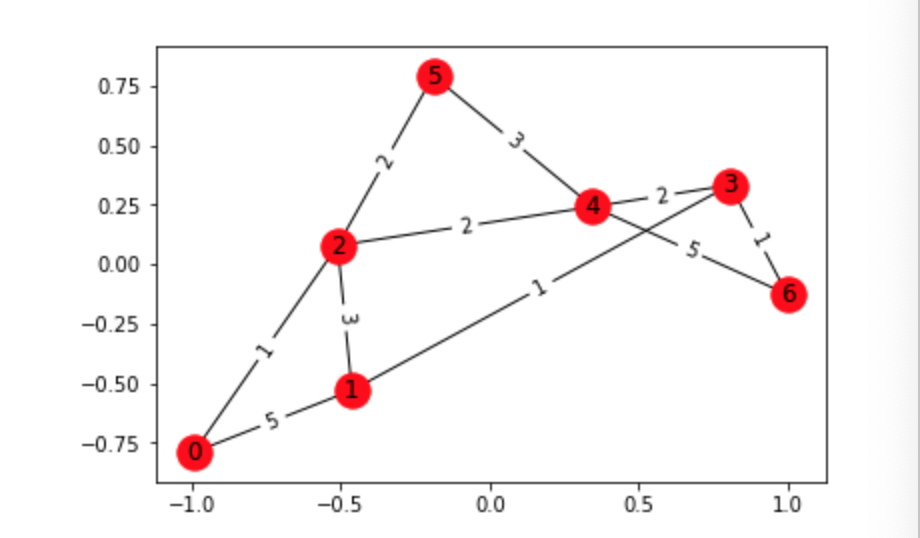
・これを使って作成した以上のグラフについて、networkxのメソッドを試していく。
・__「nx.info(G)」__とすると、グラフGの基本情報が出力される。

・__Type__はグラフの種類、__Number of nodes(edges)__は頂点(辺)の数、Average degree__は全ての頂点から出ている辺の平均数である。
・「G.nodes()」というようにすると、頂点をリスト型で取得できる。同様に、「G.edge()」とすると辺を構成する頂点をリスト型で取得できる。
・また、「G.degree()」とすると、すべての点における次数(隣接する点の数)が取得できる。
・「nx.adjacency_matrix(G)」__とすることで、Gの__隣接行列__が取得できる。ただし、返り値はリストではないので、そのままでは扱えない。以下では、重み付きグラフGについて、隣接行列を取得し、その各要素(頂点)について、__i行j列目(頂点iとj)の辺の重みが0でなければ道が存在する__ということになるので、その部分の辺について、重みを取得して、隣接リストadj_listに格納している。
・これを見ると、__「adj_matrix」には「頂点1,頂点2,重み」__というような隣接行列が作成されていることがわかる。
・__「adj_matrix[(i, j)]」で、頂点(i, j)間の辺の重みが取得できる。辺が存在しなければ0を返す、それ以外の値であれば、その値を重みとする辺が存在するということになる。よって、隣接リスト「adj_list」の「i」番目について、(j, adj_matrix[(i,j)])__として格納することで、例えばadj_list[0]の値が(1,5)であれば、「頂点0から頂点1の辺の重みは5である」という意味を持つリストが作成できる。
networkxのその他のメソッド(応用)
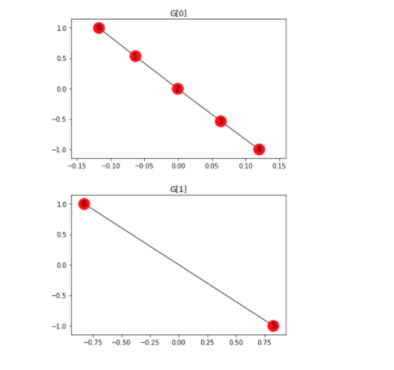
・他のメソッドとしては、グラフを__連結成分__で分割する__「nx.connected_component_subgraphs(G)」がある。「連結成分」については、次のChapterで説明する。以下では、「0~4の線」と「5~6の線」__を連結し、これで分割したものをリスト化して、前者はG[0]、後者はG[1]と、分けて描画している。

・次のメソッドは__「nx.all_pairs_dijksta_path(G)」で、これは、「ダイクストラ法」というもので、頂点間の__最短経路を求める__ことができる。最短経路は「重みが最も小さくなるような道」のことである。よって、前に行った方法で重み付きグラフを作成し、それをGとしてこのメソッドを使い、辞書型で取得すると、{i:{j:[最短経路の時に通る頂点のリスト]}}という辞書で、iからjまでの最短経路を取得できる。以下では、この最短経路の距離(重みの合計)も算出している。
・距離の求め方について、辺の重みは「edge_labels[i,j]」__で求められる。これを応用して、距離を足し合わせている。
まとめ
・__ネットワーク分析__とは、グラフ__を使ってさまざまな事象の関係について調べる分析手法である。この時のグラフ上でのそれぞれの事象を__頂点(node)、繋がりを__辺(edge)__という。
・ネットワーク分析では、__networkx__というライブラリを使用する。グラフもこれを使って作成する。無向グラフ__は「nx.path_graph()」__で作成できる。有向グラフ__は「nx.DiGraph()」で作成でき、「nx.Graph()」は条件のないグラフが作成される。
・このグラフに頂点や辺を追加していくことでグラフを作成していく。作成したグラフの描画は「nx.draw_networkx(G)」のように行う。
・グラフの辺に__重み__を付け加える時は「add_weighted_edges_from()」__を使うことで行える。また、この重みについて、__隣接行列__や__隣接リスト__に変換することで、計算などにも使えるようになる。
今回は以上です。最後まで読んでいただき、ありがとうございました。