Aidemy 2020/11/15
はじめに
こんにちは、んがょぺです!バリバリの文系ですが、AIの可能性に興味を持ったのがきっかけで、AI特化型スクール「Aidemy」に通い、勉強しています。ここで得られた知識を皆さんと共有したいと思い、Qiitaでまとめています。以前のまとめ記事も多くの方に読んでいただけてとても嬉しいです。ありがとうございます!
今回は、強化学習の二つ目の投稿になります。どうぞよろしくお願いします。
*本記事は「Aidemy」での学習内容を「自分の言葉で」まとめたものになります。表現の間違いや勘違いを含む可能性があります。ご了承ください。
今回学ぶこと
・強化学習の構成要素
・マルコフ決定過程について
・価値、収益、状態
・最適な方策について
・ベルマン方程式について
強化学習の構成要素
N腕バンディッド問題と次のステップ
・Chapter1で扱ったN腕バンディッド問題は、__「即時報酬である」点と、「エージェントの行動によって状態が変化しない」__という点で一般的な問題よりも単純化された問題であった。
・__状態__とは、環境が今現在どうなっているか__を表すものである。ボードゲームを考えるとわかりやすい。エージェントであるプレイヤーが、将棋という環境で、相手にある一手を使われた時、盤面は前の自分の番から変化しているため、次に取るべき行動も変化する。この時「盤面」という状態は変化していると言える。
・また、Chapter1でも軽く触れたが、強化学習では即時報酬ではなく、「ゲームに勝利すること」といった__遅延報酬__を最大化することが本来の目的である。
・今回は、これらの「状態」「時間」__の概念を取り込んだ強化学習を行っていく。
強化学習のモデルについて
・強化学習は、__「①エージェントが状態$s_{t}$を受け行動$a_{t}$を起こし環境に作用する」「②それを受け環境は状態$s_{t+1}$に遷移する」「③環境はエージェントに報酬$r_{t+1}$を与える」「④エージェントは②③の結果を受けて次の行動$a_{t+1}$を決定する」という流れで進められていく。
・「t」は何回目の動作かを表す「時間ステップ」__である。これが強化学習の時間の基本単位となる。
状態、行動、報酬の数式化
・環境がとりうる__状態を集合__化したものを__数式化__すると以下のようになる。
$S$={$s_{0},s_{1},s_{2},...$}
・同様に、エージェントがとりうる__行動の集合__は以下のように表す。
$A(s)$={$a_{0},a_{1},a_{2},...$}
・時間ステップ「t+1」の時における__報酬__「$R_{t+1}$」は次のように表す。
$R_{t+1}$=$r(S_{t},A_{t},S_{t+1})$
・上記のような式で報酬を求められる時、$R_{t+1}$を__報酬関数__と呼ぶ。この報酬関数から分かることでもあるが、未来の状態は現在(t,t+1)の状態・行動のみによって確率的に決定され、過去の挙動とは一切無関係である__という性質のことを「マルコフ性」__と呼ぶ。
マルコフ決定過程
マルコフ決定過程とは
・前項で見た通り、未来の状態は現在の状態や行動によってのみ決定する__ということを「マルコフ性」と呼ぶ。そして、これを満たす強化学習の過程を「マルコフ決定過程(MDP)」という。
・マルコフ過程は、状態の集合「状態空間$S$」、行動の集合「行動空間$A(s)$」、開始時点の状態を表す確率変数「初期状態分布$P_{0}$」、状態$s$で行動$a$を行った時、状態$s'$になる確率の変遷率を「状態遷移確率$P(s'|s,a)$」、「報酬関数$r(s,a,s')$」__の五つの要素を持つ。
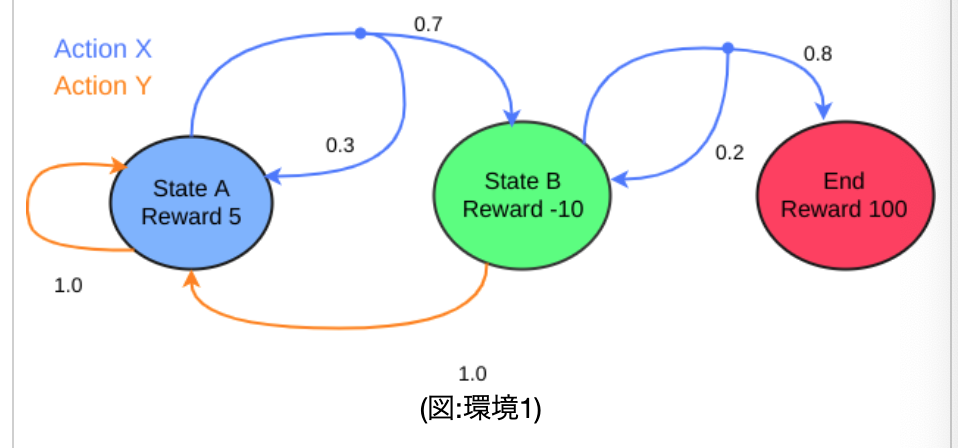
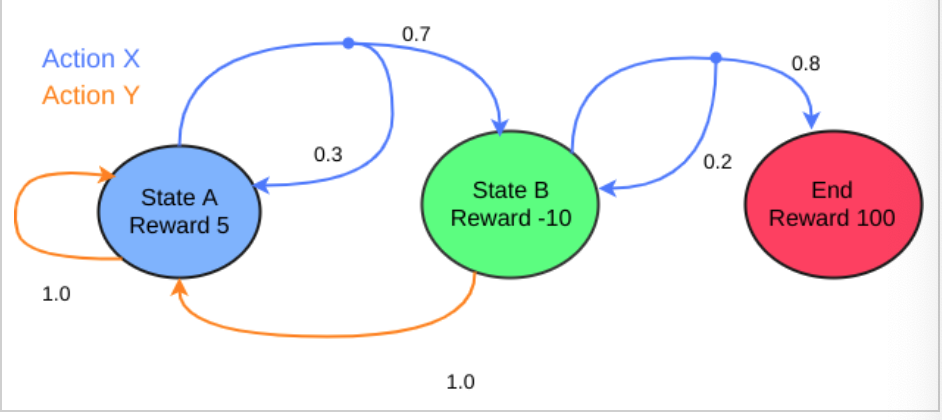
・以下の図は、今回使っていく環境__「環境1」__である。StateAからスタートし、actionXを取る場合「0.7」の確率でStateBに移動し、「0.3」の確率でStateAに戻るということが示されている。最終的に、StateBで、actionXの「0.8」を引ければゴール(End)となる。
・この各場合において、上記5要素を__[s,s',a,p(s'|a,s),r(s,a,s')]というように表したものを「状態遷移図」__という。(sは今どの状態か、s'は次にどの状態にいくか、aはactionXかYか、p(s'|a,s)は、その確率、r(s,a,s')はその報酬である)
・以下のコードは、この環境1のすべての状態遷移図を配列としてまとめたものである。配列にする際は、__StateA=0、StateB=1、End=2__のように数値で置き換える。
時間の概念を導入-状態と行動
・マルコフ決定過程の構成要素である前項の五つの変数には、まだ__時間の概念が導入されていない__ので、これらの時間の概念を導入し、数式化を行う。
・状態空間__S__について、時間tの概念を入れた「$S_{t}$」と、行動に時間の概念を導入した「$A_{t}$」を定義する。
・定義において使われるのは、前項の__「状態遷移図」の配列である。この配列の__0列目__は「state」つまり「今(t時点)の状態」であるので、これが「$S_{t}$」_となり、2列目__は「action」つまり「t時点の行動」であるので、これが「$A{t}$」_となる。
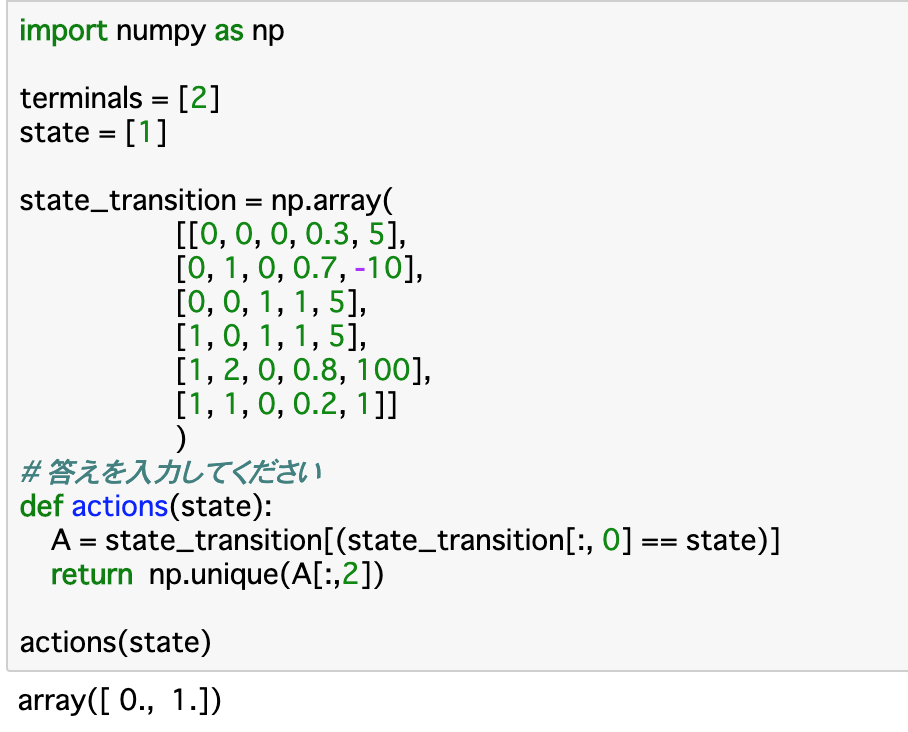
・以下は、$S{t}$が渡された時、_その状態でエージェントがとりうる行動__をまとめた$A{t}$を返す関数である。
・「actions()」関数に渡される「state」が状態「$S{t}$」であり、Aで参照される「state_transition」が__状態遷移図__である。この0列目が「$S{t}$」なので、この部分が渡されたstateと同じ状態のものを参照することを記述し、「A[:,2]」で2列目を参照することでその時にとりうる行動$A{t}$をリストにして返す。この時、返り値は可能な行動であるので、重複してはいけない、つまり__固有の要素__でなければならない。これを行うには_「np.unique()」__を使うと良い。
・実行部分について、今回の状態はStateBにいることを示す__「state=[1]」__となっている。state_transitionのs部分(現在の状態)、つまり0列目が[1]の行の2列目を見ると、0か1が格納されているので、関数の結果としては、これらが返される。
時間の概念を導入-その他
・ここでは初期状態分布と状態遷移確率、報酬関数を時間の概念を取り入れて再定義する。
・初期状態分布は簡単で、t=0__の時の状態$S{0}$を定義すれば良い。
・状態遷移確率は__マルコフ決定過程__により、時刻$t+1$における状態$S{t+1}$は$S_{t}$と$A_{t}$によってのみ決定するものなので、$P(s'|s_{t},a_{t})$というように表せる。
・状態$S_{t+1}$に遷移したときの__報酬__$R_{t+1}$について、$R_{t+1} = r(s_{t},a_{t},s_{t+1})$で表せる。
この報酬関数について定義したのが、以下のコードである。
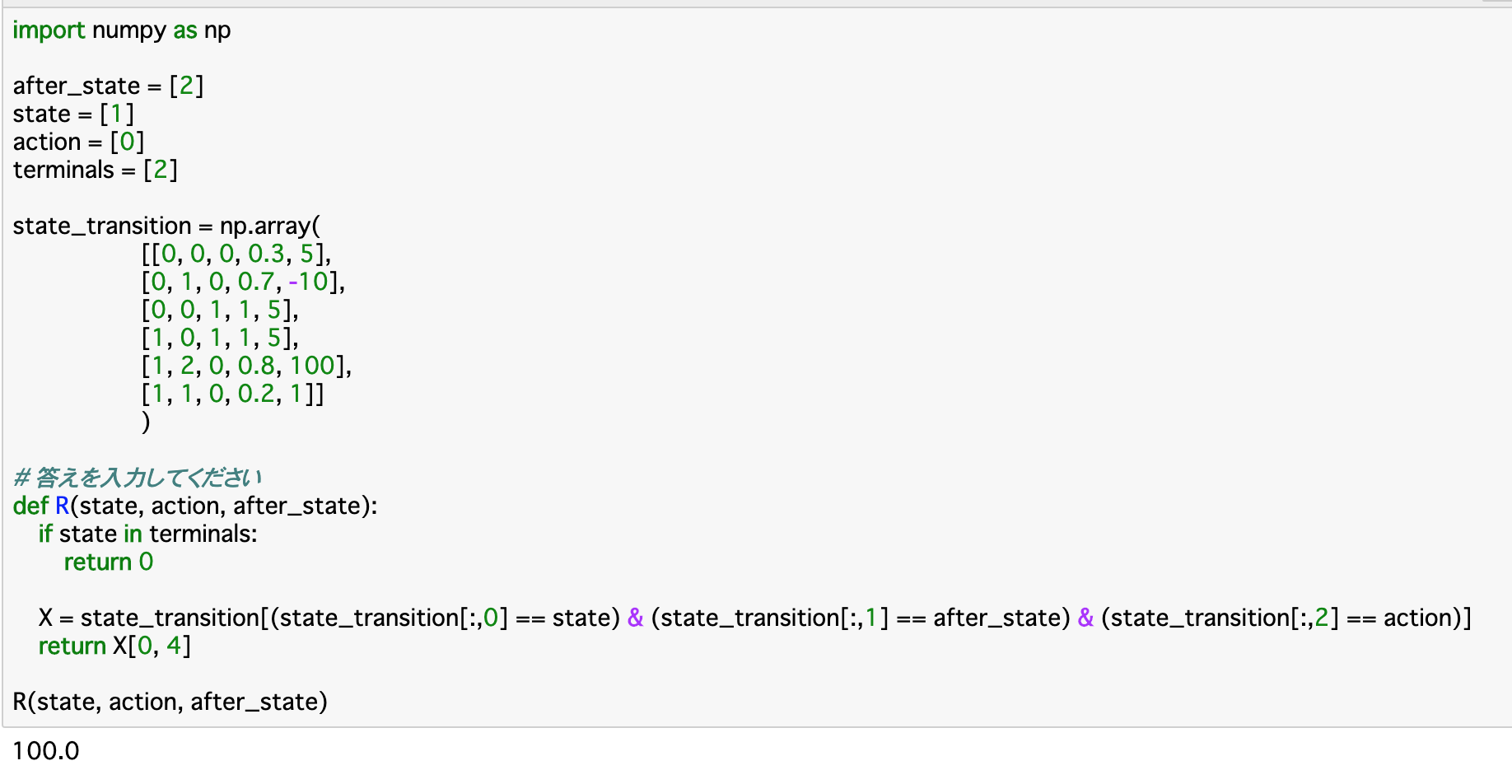
・この関数__「R」について、引数では先述した$s{t},a{t},s_{t+1}$の三つを渡す。前提として、__既に終点(terminal)にいる時__は報酬が存在しないので、__0__を返す。
・今回も「state_transition」を参照して報酬を返すのであるが、__報酬__はこの配列の__4列目にある__ので、条件にあった状態(行)を抽出して、その4列目を返すようにすれば良い。
・今回の条件とは、引数で渡された「state,after_state,action」について、それぞれが一致するものをstate_transitionの0,1,2列目から探し出せば良い。
・実行部分について、stateが[1]、after_stateが[2]、actionが[0]となっているので、__「現在StateBにいて、ActionXを行うことでEndについた」__時の状態遷移を参照すれば良い。今回のstate_transitionでいうと、それは__4行目__の [1, 2, 0, 0.8, 100]であるので、この4列目の報酬が出力されている。
エピソード
・タスク開始から終了までにかかる時間のことを__「エピソード」という。「行動→状態変化」というサイクルが何度も続くことによって時間ステップが進んでいき、一つのエピソードが構成されていく。
・強化学習のモデルでは、この一つのエピソードについて「環境を初期化し、エージェントに行動させ、受け取った報酬を元に行動モデルを最適化する」__ということを__複数回行う__ことで学習を進めていく。
・ターン性のカードゲームなどが例として非常にわかりやすい。ターンごとにプレイヤーの行動によって盤面は変化していき、「勝敗」という形でタスクが終了する。これを一つのエピソードとして、何度も対戦を行うことで、次第に最適な手を学習していくようになる。
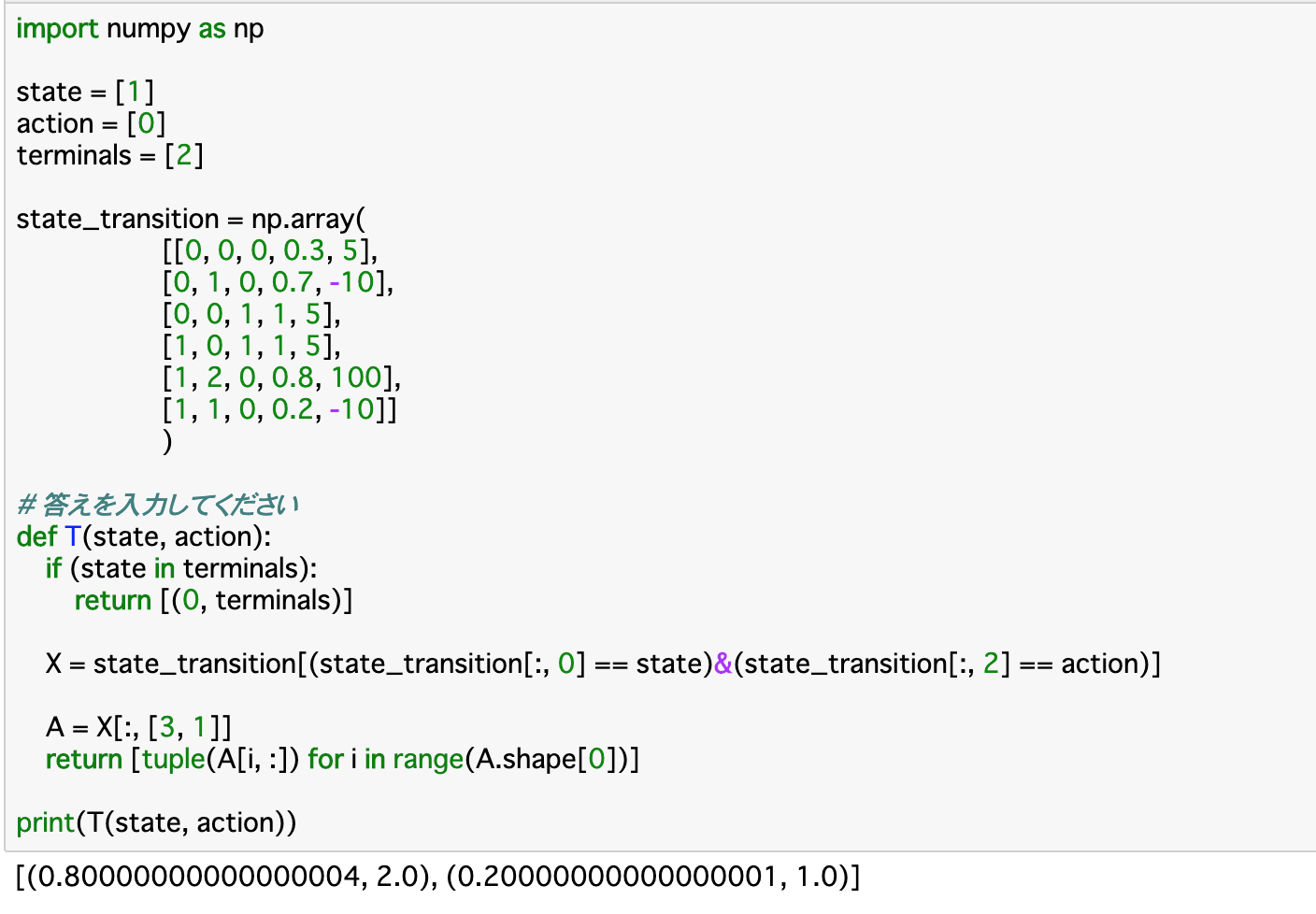
・以下はエピソードを定義した関数__「T()」である。この関数は「現在のstateとactionを渡し、state_transitionから対応するものを抽出し、状態遷移確率と遷移後のstateを返す」__というものである。
・Tの定義部分について、__既に終点(terminals)にいる時__は、状態が遷移することはないので __[(0, terminals)]__と返すようにする。
・X__については前項と同様に、渡された引数と一致する行を抽出している。この行の「3列目(状態遷移確率)」と「1列目(遷移後のstate)」をAに格納し、とりうる全ての場合について「tuple(A[i,:])」__でタプル化して返す。
価値・収益・状態
報酬と収益
・ここまでは強化学習のモデル化、定義を行ってきた。ここからは__「何を基準に最適な方策を探っていくか」ということを考える。
・報酬__を指標にして考えた場合、これは__直前の行動のみ__によって決まってしまうので、「その時点ではほとんど価値のない行動でも、その後非常に大きな価値を持つ行動」を見落としてしまう。
・これを解決するのが「収益」である。収益は__ある期間に得られた報酬の合計__で算出されるため、その状態より__後の報酬も考慮に入れることができる。
・t時点での行動$a{t}$によって得られる報酬を_「$R_{t}$」とすると、ある期間内の報酬の和である収益「$G_{t}$」は次の式で算出できる。
$$
G{t} =R{t+1} + \gamma R_{t+2}+ \gamma^2 R_{t+3}+....= \displaystyle\sum_{\tau=0}^{\infty} \gamma^{\tau} R_{t+1+\tau}
$$
・$\gamma$は__「割引率」と呼ばれ、(0〜1)の値をとる。これは、「将来もらえる報酬をどれぐらい現在の価値とするか」__を表すもので、0に近いほど将来の価値を見出さないようになり、1に近いほど将来の価値に重みをつけるようになる。
・また、報酬の合計の算出にはいくつか手法が存在するが、一般的には__「割引報酬和」__というものが使われる。これは__時刻tからある時刻Tまでの収益の平均__を算出し、__Tの極限を取る__ことで算出する、というものである。
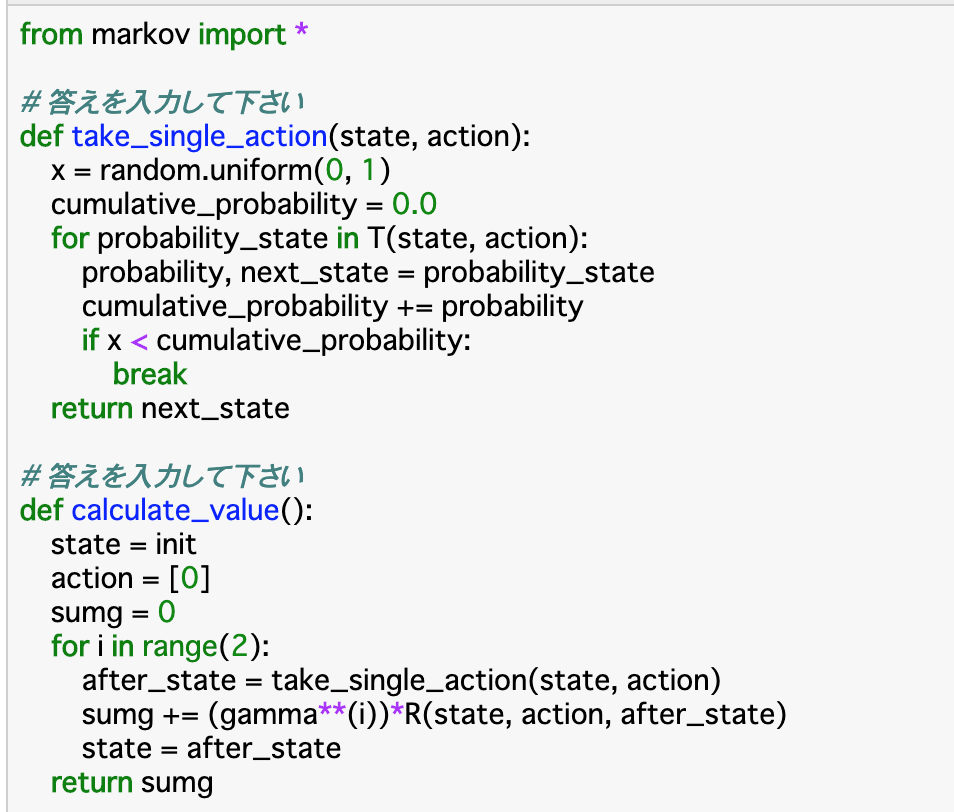
・割引報酬和は、以下のように二つの関数で定義することができる。
・__「take_single_action()」について、これは「遷移確率に基づいて次の状態を決定する」関数である。コードとしては、まず「random.uniform(0,1)」__で0〜1の乱数を生成する。また、__累積確率「cumlative_probability」を定義する。
・for文では渡されたstate,actionからエピソード「T」ごとに、考えうる確率「probability」と次の状態である「next_state」__を抽出し、累積確率「cumlative_probability」にエピソードごとの「probability」を足し、これが「x」より大きくなったらfor文を終了させ、その時点での「next_state」を返す。
・もう一つの関数__「calculate_value()」について、これが「割引報酬和」__を計算する関数になる。はじめに「state」「action」と、__割引報酬和「sumg」__を定義する。
・for文では、__エピソードの回数分の繰り返し__を行う。今回は2回としている。この中で、次のstate__を「take_single_action」で定義し、これと、その時の「state」「action」_を使って$R{t+1}$を計算し、これと$\gamma^i$をかけたものを__sumgに累積__していく。そして「state」を更新したら次のエピソードにいき、最終的な割引累積和「sumg」を返す。
価値関数・状態価値関数
・前項のやり方のように、__報酬を方策の評価基準とする__ようなやり方では、Rが確率に基づいて決定するため、__状態が分岐すればするほど複雑な計算式になってしまう__という欠点がある。
・__報酬の期待値__を取ることで、以上の欠点を解消できる。ある状態をスタートとして、それ以降の行動全てを考慮に入れた報酬の期待値__のことを、「価値」または「状態価値」__という。方策が良いものであればあるほど状態価値は大きくなる。
・この概念を導入することで、「ある方策において、どの状態が優れているか__を比較できる」「ある状態をスタート地点に置いた時の__方策ごと良し悪しを比較できる」という二つのことが可能になる。
最適な方策の探索
最適方策
・前項の__状態価値関数__の導入により、方策ごとの良し悪しを比較__できるようになった。
・二つの方策$\pi{1},\pi{2}$を比較する時
・状態空間Sの全ての状態sにおいて、状態価値$V^{\pi_{1}}(s)$が$V^{\pi_{2}}(s)$以上__である
・状態空間Sの少なくとも一つの状態sにおいて、状態価値$V^{\pi{1}}(s)$が$V^{\pi{2}}(s)$より大きい
の二つが成り立つ時、__「$\pi_{1}は\pi_{2}$よりも良い方策である」__ということができる。
・また、この時全ての方策の中には最も良い方策が存在するはずであり、これを__最適方策__と呼び、$\pi^*$と表す。
行動価値
・状態価値関数は__「ある状態をスタートとした時の報酬の期待値」__であるが、実際には「ある状態をスタートとし、__ある行動を起こした時の__報酬の期待値」というように、行動__まで考慮に入れた価値を考えた方が良い場合が多い。この時の価値を「行動価値」といい、ある方策下における行動価値を示す関数を「行動価値関数」__という。
・行動価値関数は、__各「行動」がどれだけ良いか__を判断する関数ということができる。
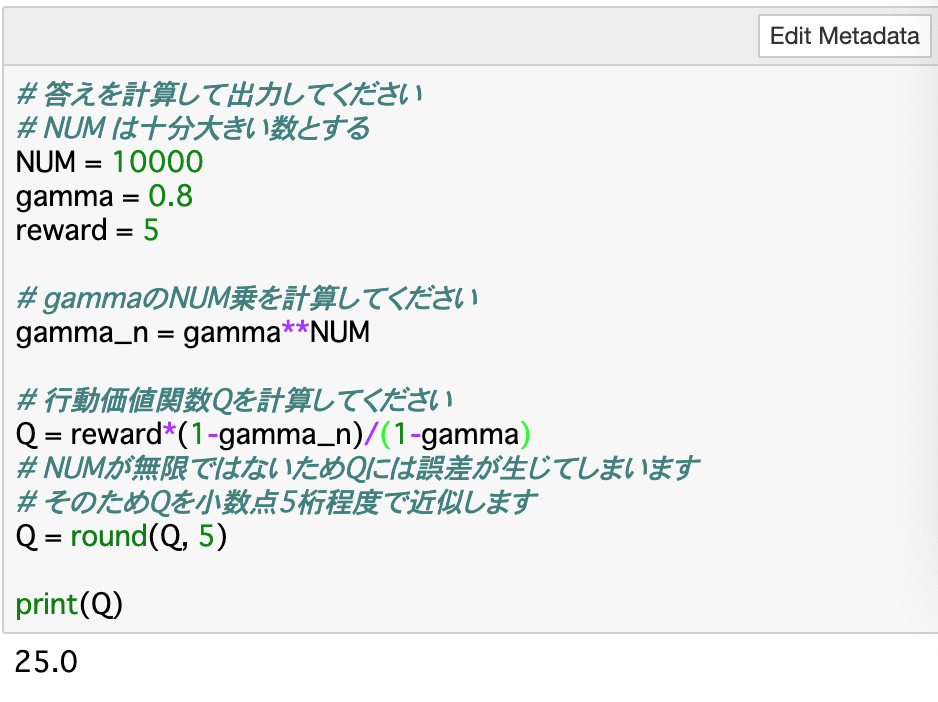
・数式としては、以下の__等比級数__の公式を使用する。
$$a+ar + ar^2 + \cdots + ar^n = \large\frac{a(1 - r^n)}{1 - r}$$
・この公式の「a」をreward(報酬)、「r」をgammaとして、行動価値関数を計算することができる。これについてのコードが以下のようになる。
最適状態価値関数・最適行動価値関数
・ここまでに見てきた「状態価値関数」と「行動価値関数」のうち、最適な方策に従った場合のそれぞれの関数を__「最適状態価値関数」「最適行動価値関数」という。それぞれ、「$V^*(s)$」「$Q^*(s)$」と表す。
・一度最適状態価値関数と最適行動価値関数が求められれば、どの行動が最も収益の大きくなる行動かがわかるということなので、常に最適な行動を選び続ける「greedy手法」__を選べば良い。
ベルマン方程式
最適な状態価値
・__最適状態価値関数を求める__には、__それぞれの状態価値関数を求め、比較__すれば良い。行動価値関数についても同様であるので、ここでは状態価値関数を対象に進めていく。
・それぞれの状態価値関数の求めるには、ベルマン方程式__を使う。これは「状態sと行動した結果移行する可能性のある状態s'との間に価値関数の関係式を成り立たせる」という発想から成り立つ。
・ベルマン方程式は以下のようにそれぞれの関数を__漸化式__のようにすることで使用できる。
$V^{\pi}(s) =\displaystyle\sum{\alpha \in A(s)}^{} \pi(a|s) \displaystyle\sum{s' \in S}^{} P(s'|s,a)(r(s,a,s') + \gamma V^{\pi}(s'))$
$Q^{\pi}(s,a) =\displaystyle\sum_{s' \in S}^{} (P(s'|s,a)
(r(s,a,s') + \displaystyle\sum_{a' \in A(s')}^{} \gamma \pi(a'|s') Q^{\pi}(s',a')))$
・ここでの$\pi(a|s)$ は、__行動の選ばれる確率__を表している。
・例えば「環境1」において、__「s=StateB」、「$\gamma$=0.8」、「ActionXのみを行う」とするとき、ベルマン方程式で価値関数を算出すると
$V^\pi(B)=0.2(-10+\gammaV^\pi(B))+0.8(100+\gamma0)$を$V^\pi(B)$についての方程式として解けば良い。
すなわち、より簡単にいうと、「(そのActionを起こす確率) × (行動によるReward + $\gamma$ × 移動後のState)」__を全ての場合について算出し、その__和__を使って方程式を解けば良い。
ベルマン最適方程式
・先述した最適状態関数、最適行動関数についても、当然にベルマン方程式が適用できる。よって、常に最適な方策をとった時のベルマン方程式__を「ベルマン最適方程式」という。
・例えば環境1で「常にActionXをとる方策$\pi{1}$」「常にActionYをとる方策$\pi{2}$」のどちらがいい方策であるかを比較するとき、__収益(割引報酬和)を算出する関数「caluclate_value()」__を使って、以下のように表せる。
・__Q_optimum__はその時の最大の収益を表し、__Q_pi__はその時の方策を表している。Q_piが[0 0]となっていることから、_常にActionXを取る__方策$\pi{1}$を取る方が良いことがわかる。
まとめ
・時間ステップ「t+1」の時における報酬「R_{t+1}」は $r(S_{t},A_{t},S_{t+1})$と表される。この時未来の状態(t+1)は現在の状態や行動(t)によってのみ決定されることを「マルコフ性」といい、これを満たす強化学習の過程をマルコフ決定過程という。
・マルコフ決定過程において、構成要素を[s,s',a,p(s'|a,s),r(s,a,s')]というように配列で表したものを「状態遷移図」という。時間の概念を導入した場合は$[S_{t},S_{t+1},A_{t},S_{0},R_{t+1}]$で表される。
・タスク開始から終了までの時間のことを「エピソード」という。強化学習ではこのエピソードについて「環境を初期化し、エージェントの行動による報酬をもとに最適化する」ことを繰り返して学習を行う。
・実際の強化学習では、即時報酬だけでなく、遅延報酬も含めた「収益」を基準に最適な方策を考える。収益は、各時間ステップにおける報酬に「割引率$\gamma$」をかけたものの和である「割引報酬和」で計算する。
・また、最適な方策を探索するにあたっては、収益についてこのまま計算すると計算量が多くなってしまうので、報酬の期待値である「状態価値関数」「行動価値関数」を計算すると良い。これらを求めるときに使われるのが「ベルマン方程式」である。状態価値関数についてベルマン方程式を使うとすると、「Actionを起こす確率」「報酬」「移動後のState」を使って算出される。
今回は以上です。ここまで読んでくださりありがとうございました。