p値と有意水準αの関係を視覚的に理解する

#マーケティングの実務で使えるデータサイエンス
※I'm quite welcome to get your feedback or MASAKARI..

#序論

　RやPythonのライブラリでは, Excelレベルの関数の記述によって, 手を煩わせずにt検定やカイ二乗検定などの統計的仮説検定を実行できる. ただ, p値や仮説検定における有意水準αを本質的に理解するためのコストは変わっていない. ここでも "There is no free lunch" は普遍的である.

　私は何かを理解する時, まずイメージ(視覚情報)をインプットすることでその外観を掴むようにしている. そこで今回は「p値とは何か?」を理解する道のりの途中で, イメージでp値の正体を把握することで, より解像度高いp値の理解につながるようなコンテンツを生産してみたかった.

　まずp値と有意水準αをグラフィカルに理解するためのキーワードは, 「累積確率」である. 結論から言うと, p値も有意水準αも本質的には各統計検定量が従う分布(確率密度関数)における, 累積確率(区間積分の概念)に他ならない.
　
　またp値は「危険率」と表現されることもあり, このニュアンスを押さえておくことも有意水準αとの関係を理解する上で助けになるだろう.

###対象読者

　統計の専門家ではなく初学者であり, WEB/アプリ系の企業で働いている...

• データアナリスト
• データサイエンティスト
• マーケター

###統計理論

• t検定(Welchのt検定)
• p値
• 有意水準α

###使用言語

• R

#本論

###構成

1. 検定統計量tとt分布
2. 有意水準αと第1種の過誤
3. p値と有意差

###前提: スコープについて

　本文は徹底して実務を想定して書いた. 企業における統計ユーザーがp値に触れる機会は主に, A.仮説検定とB.回帰分析の2つだとする. そこで今回はA.仮説検定におけるp値を主題として扱う.

　また, 2標本の平均値の有意差を統計的に検証するためのt検定の種類は複数ある. その中で今回は, 「対応の対応のない&等分散ではない」場合に多く用いられる「Welchのt検定」における「片側検定」を対象とする.

　なぜここで「Welchのt検定」を扱うかというと, 一重にWeb/アプリサービス関連企業で働くデータ分析者がt検定を行うシーンで最も実用的かつ必然的な選択肢だと考えるからだ.

　さらに, UIデザインのABテストなどではどちらのグループの平均値が大きいかは既知な上で, その差が統計的に有意か否かが知りたい状況が多いと考え, あえて「片側検定」を選択した.

　前提として, 仮説検定の手続きや帰無仮説とは何かなどを改めて説明することはしない.

　なので全体的な仮説検定のプロセスを時折飛ばしてp値や有意水準のみに話が飛躍/フォーカスする可能性がある点をご了承頂きたい.

##1. 検定統計量tとt分布

　まずはp値を理解するために必要な前提知識として最も重要な「検定統計量」と検定統計量が従う「分布(確率密度関数)」を抑える.

　具体的には, p値はt値の大小によって決まってしまうため上記の2つを抑えればp値そのものの理解(有意水準などは別)は難しくない.

　平均値を扱う具体例として, 今回はとある化粧品販売Webサイトの商品紹介ページを扱う.

　いま既存デザインAと新規デザインBの入れ替えを検討しており, ユーザーの平均滞在時間を基準にどちらを採用するか判断しようとしている.

　そこでA/Bテスト(RCT)によってサンプルから手に入れた, 2つの平均滞在時間の間に統計的に有意差があるかを確かめたい.

　ではまず, デザインA/Bにおける各ユニークユーザーの滞在時間のサンプル(リスト)を作成する. また同時に, 各デザインにおける平均滞在時間も計算する.

#ABテスト: ListページABにおける平均滞在時間データ
a <- c(34,56,65,43,43,65,66,43,19,21) #デザインAにおけるユーザーの滞在時間サンプル
b <- c(87,54,45,41,33,25,96,46,32,76,32,54) #デザインBにおけるユーザーの滞在時間サンプル

#平均値を算出
mu_a <- mean(a)
mu_b <- mean(b_new)

print(mu_a)
print(mu_b)

• デザインAの平均値: 45.5
• デザインBの平均値: 51.75

　いま2つの平均値が手に入った. 次は, 検定統計量t値の導出に移る.

　Welchのt検定における統計検定量tは以下の式で求められる. なお, t値の算出式は対応のある/なしなどに応じたt検定の種類によって異なる. 　　
　

t=\frac{\bar{X}_a-\bar{X}_b}{\sqrt{\frac{U^2_a}{n_a}+\frac{U^2_b}{n_b}}}

　　
　ここでt値を直感的に理解するために, まずは分子のみに注目するといい. 一旦シンプルに, 検定統計量t値は2群の平均値の差の大小を表す値だと考える.

　基本的に有意差がある場合は, 差の絶対値が極端に大きい→t値も極端に大きい/小さい→2群の平均値には有意な差があるといった論理の展開が期待される.

　厳密には, 分母は不偏分散とサンプルサイズによって構成される. 分母なので, 不偏分散(バラツキ)が小さいほど, またはサンプルサイズ(信頼性)が大きいほどt値が大きくなる構造になる.

　では実際にt値を算出してみる. 上記のt値の式を見ると, Welchのt検定におけるt値が以下の3つの要素で構成されていることがわかる.

• X¯: 平均値×2
• n: サンプルサイズ×2
• U^2: 不偏分散×2

　それでは各群ごとに, 今手元にないサンプルサイズと不偏分散を用意し, t値を算出する.　

#サンプルサイズ
n_a <- length(a)
n_b <- length(b)

#不偏分散
sigma_a<-0
for (i in a) {
    sa=(i-mu_a)**2 #偏差の平方
    sigma_a=sigma_a+sa
}
uv_a<-sigma_a/(n_a-1)

sigma_b<-0
for (i in b) {
    sb=(i-mu_b)**2 #偏差の平方
    sigma_b=sigma_b+sb
}
uv_b<-sigma_b/(n_b-1)

#t値を求める
t<-(mu_a-mu_b)/sqrt((uv_a/n_b)+(uv_b/n_b))
print(t)

• t値: 0.722948

　次に, このt値は帰無仮説と対立仮説においてそれぞれ「分布」を有する. 具体的にはt値は, 自由度dを唯一のパラメータとするt分布に従う. また, t分布の期待値E(X)と分散V(X)は以下となる.
　

E(X)=0　(d>1)

V(X)=\frac{d}{d-2}　(d>2)

　　
　それでは自由度dを算出する. 自由度dは, サンプル数nと不偏分散U^2から求められる. 今回は説明の便宜上, 下記から計算される自由度dの小数点を切り捨て, 整数として扱う.

d <- floor((uv_a/n_a)+(uv_b/n_b))**2/((uv_a**2/((n_a**2)*(n_a-1))) + (uv_b**2/((n_b**2)*(n_b-1))))
print(d)

• 自由度d: 19

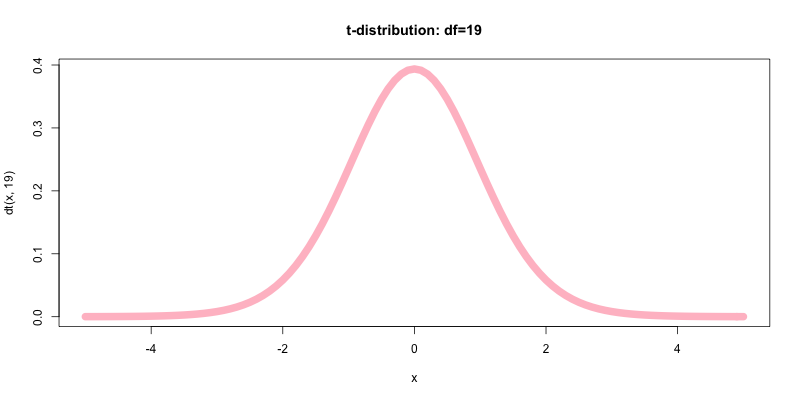
　 ようやくt分布のパラメータの値が定まったので, 自由度d=19のt分布を可視化する.

curve(dt(x, 19),-5,5,type="l", col="pink", lwd=10, main="t-distribution: df=19")

これでt値の算出とt分布のパラメータの特定が完了した. 後述するが, 最初に求めたt値(0.722948)は, この自由度d=19のt分布の確率密度関数(PDF)のx軸上にプロットすることができる.

　次に, 有意水準αの解説に移る.

##2. 有意水準αと第1種の過誤

　今回は, 帰無仮説の片側検定における棄却域の有意水準をα=0.05(5%)と設定する.

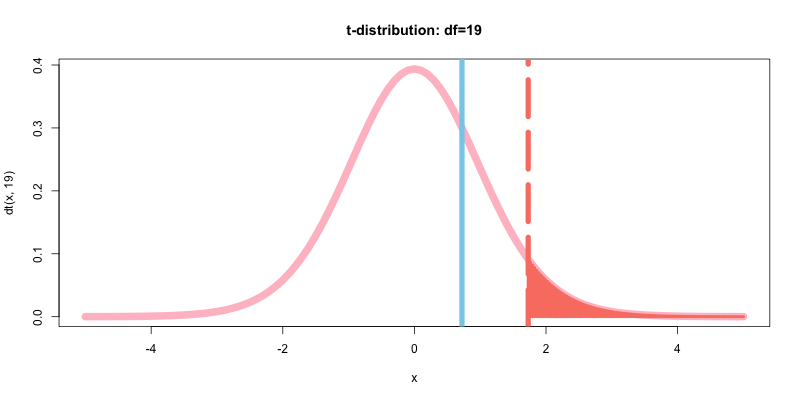
　まず自由度d=19のt分布において, 棄却域となる有意水準5%の確率(赤色塗りつぶし部分の面積)と有意水準の閾値(赤色の直線)を可視化して理解してみる.

　余談になるが, 面積と確率の関係はこちらでわかりやすく解説されている.

curve(dt(x, 19),-5,5,type="l", col="pink", lwd=10, main="t-distribution: df=19") 
abline(v=qt(p=0.95,df=19), col="salmon", lwd=7, lty=5)
curve(dt(x, 19),qt(p=0.95,df=19),5,type="h", col="salmon", lwd=4, add=T) 

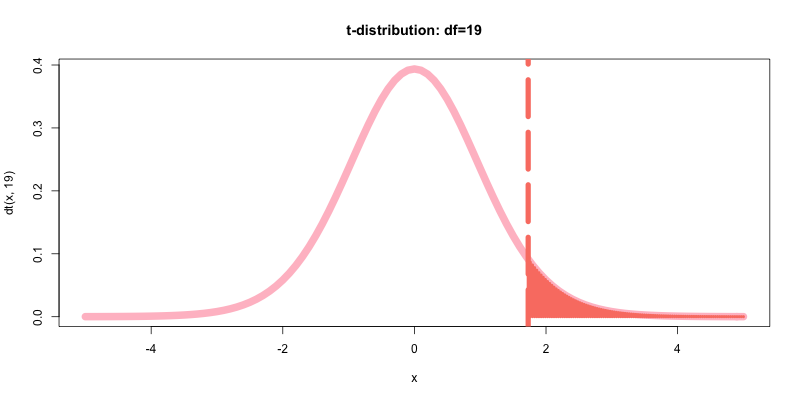
　今, 有意水準α=0.05(累積確率)を表すなお赤色の点線で表された棄却域の閾値はt=1.729であり, このことはt分布表を見れば確認できる.

　ここで本題ではないが, 検定に必要なサンプルサイズを求める際などに出会う「第1の過誤」という概念と有意水準の関係にもせっかくなので少し触れる.

　第1の過誤(Type1 error)の辞書的な説明はこちらに譲るが, 簡単に翻訳すると本検定において本当は2つの平均値に差がない(帰無仮説)のに, 誤って差がある(帰無仮説の棄却)としてしまう確率のことである.

　有意水準とはまさに「第1の過誤」を犯してしまう確率を指している. 有意水準αを0.10から0.05に下げる理由は, この第1の過誤(差がないのにあるとするリスク)を犯す確率を下げたいからに他ならない.

　なので, 有意水準を調整することはつまり, 検定の厳密さ(リスクの許容範囲)を調整しているということである.

　さいごに先ほど求めたt値をプロットし, 有意水準の閾値との関係を可視化してみる.

curve(dt(x, 19),-5,5,type="l", col="pink", lwd=10, main="t-distribution: df=19") 
abline(v=t, col="skyblue", lwd=7)
abline(v=qt(p=0.95,df=19), col="salmon", lwd=7, lty=5)
curve(dt(x, 19),qt(p=0.95,df=19),5,type="h", col="salmon", lwd=4, add=T) 

##3. p値と有意差

　次にp値を計算・可視化する. 最初に述べたが, p値は累積確率であることをここで確認したい.

　t値とp値には密接な関係がある. p値は, t値の大小によって決まる.

　具体的には, p値はt値(≒平均値の差分)の絶対値と反比例の関係にある(こと片側検定においては確実に). つまり差分が大きいほど, p値は下がる. それではp値を図示してみる.

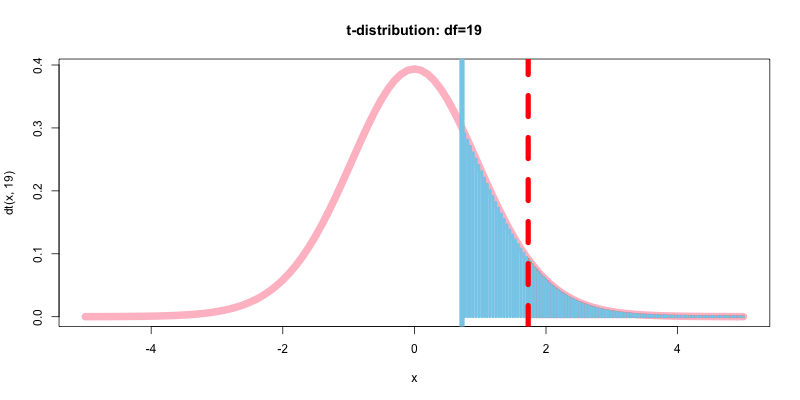
curve(dt(x, 19),-5,5,type="l", col="pink", lwd=10, main="t-distribution: df=19") 
curve(dt(x, 19),qt(p=0.95,df=19),5,type="h", col="salmon", lwd=4, add=T) 
abline(v=t, col="skyblue", lwd=7)
curve(dt(x, 19),t,5,type="h", col="skyblue", lwd=4, add=T) 
abline(v=qt(p=0.95,df=19), col="red", lwd=7, lty=2)

p_value<-1-pt(q=t,df=19)
print(p_value)
>>> 0.2392588 # p値 > 0.05(有意水準α=5%)

• p値: 0.2392588
  

　水色で塗りつぶされた部分がp値である. 厳密にはp値は, 「水色で塗りつぶされた面積(区間積分)」/「確率密度関数全体の面積」の割合で算出される値である.

　図から解るように, この例ではp値を示す水色の面積の方が, 有意水準αを示す赤色の面積よりも大きくなった. これこそがあの「p値>0.05なので帰無仮説を採択する」ということを可視化したものだ.

　言い換えるとt値が棄却域にない, あるいはp値が有意水準α(第1の過誤を犯す確率)を上回るため「2つの平均値の差に統計的な有意差はない」という帰無仮説を採択することを意味する.
　
　また上記から仮に不偏分散(U^2)とサンプルサイズ(n)が一定だった場合, 2つの平均値の差がより大きくなると, 今回の場合だとt値がより正の方向に大きくなり(右に移動), p値は小さくなることがわかる.

　そして, p値を表す面積が有意水準の面積(全体の5%)よりも小さくなれば, 帰無仮説を棄却し統計的な有意差が認められることになる.

　いかがだっただろうか? これでp値とは何か?, そしてp値と有意水準の関係は?という問いへの一時回答を終了する. 以降は, 帰無仮説が棄却される(差がないことの否定)ケースを見ていく.

###再検定: 有意差がある(t値が棄却域にある)場合

　ここで試しに先ほどのBのサンプルの値のいくつかをより大きな値に変え, 滞在時間の平均値をより大きくして再度検定することにする. *便宜上自由度については, 小数点以下を切り捨てた自由度d=19で統一した

　それでは, 先ほどのBの配列内の値をより大きな値で上書きしてみる.

b <- c(87,34,35,41,79,78,66,73,68,63,71,54)
mu_b <- mean(b)
... #前述と同様なので省略
t<-(mu_b-mu_a)/sqrt((uv_b/n_b)+(uv_a/n_a)) #Aとのt値を求める
print(t)
>>> 2.249326

• t値: 2.249326

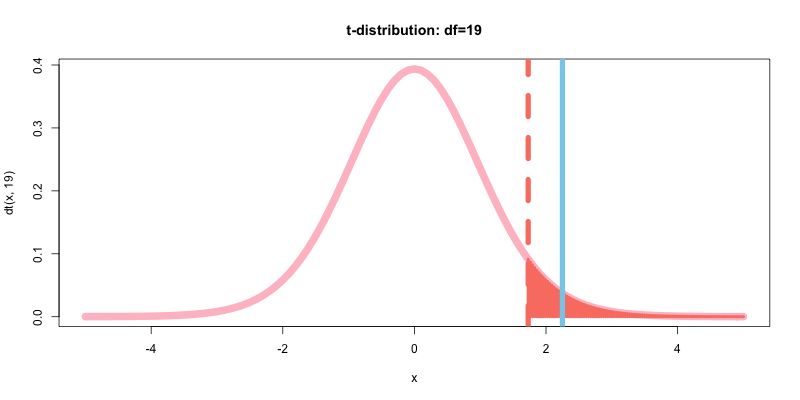
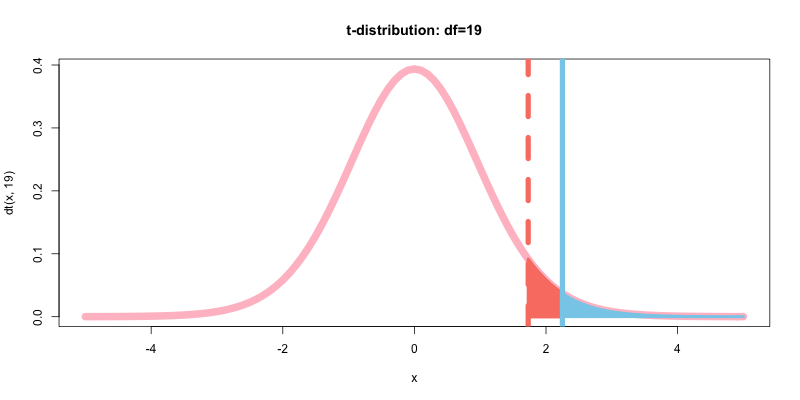
　改めて自由度d=19のt分布と先ほど求めたt値を可視化する(t値は水色の直線とx軸が交わる点).

curve(dt(x, 19),-5,5,type="l", col="pink", lwd=10, main="t-distribution: df=19") 
abline(v=qt(p=0.95,df=19), col="salmon", lwd=7, lty=2)
curve(dt(x, 19),qt(p=0.95,df=19),t,type="h", col="salmon", lwd=4, add=T) 
abline(v=t, col="skyblue", lwd=7)
curve(dt(x, 19),t,5,type="h", col="skyblue", lwd=4, add=T) 

　改めてp値を求め, その累積確率を可視化する. p値の計算における補足として, 今回の場合はp値は右側を始点とした累積確率, つまり「1-左側を始点とした累積確率」で求めている.

p_value<-1-pt(q=t,df=19)
print(p_value)
>>> 0.01827168 #p値 < 0.05(有意水準α=5%)

• p値: 0.01827168
  

　上記から, 今回のp値=0.01827168は検定初期に設定した有意水準α=0.05を下回る結果となった.

　よって, 今回のt値(p値)は, 第1の過誤を犯すリスクの基準値(有意水準)よりも小さな場所にありますよということを意味する. つまり許容できるリスクの範囲内にp値が収まったと言える.

　以上で, 仮説検定(Welchのt検定)において, 有意差が認められる場合の検定を終了する.

#結論

　最後に, タイトルにある「p値と有意水準αの関係」とは結局なんだったのかという点をまとめる.

• p値は, 統計検定量が従う分布における「累積確率」である
• p値は, 検定統計量の値の大小(極端さ)で決まる
• p値は, 有意水準α(第1の過誤を犯す確率)よりも小さな値となったとき帰無仮説は棄却される

　また, ソフトウェアのソースコードにアルゴリズムがあるように, 物事の理解にも適切なアルゴリズム(手順)が必要だろう. こと仮説検定におけるp値のより本質的な理解に向けては, 以下3つの周辺情報を先に抑えることをお勧めする.

• **統計検定量(t値やz値)**という値が存在すること
• 統計検定量はある**分布(t分布やカイ二乗分布)**に従うこと
• 有意水準αとは, **第1の過誤(Type1 error)**という概念と結びついていること

　今回はp値と有意水準αのグラフィカルな説明に挑戦した. 繰り返しになるが, 仮説検定の棄却(否定の度合い)や第1の過誤などの厳密な意味やニュアンスは理解し難いものがある. なのでまずは, 極端な理解でいいという割り切りのもと今回は書いている.

　次回は, 有意水準αと検出力(1-β)の関係について説明をしていきたい.
　
##参考文献

• What a p-value tells you about statistical significance
• StatQuest: P Values, clearly explained
• 仮説検定の概念