３層ニューラルネットワークを実装する

本記事は、ゼロから作るDeep Learningの学習メモです。　　

要点

• 活性化関数：
  入力信号の総和がどのように活性化するか（発火するか）を決定する役割を持つ。
  パーセプトロンでは閾値を境に出力が切り替わる「ステップ関数」が使用されるが、ニューラルネットワークでは滑らかな曲線を描く「シグモイド関数」や「ReLU関数」などが用いられる。
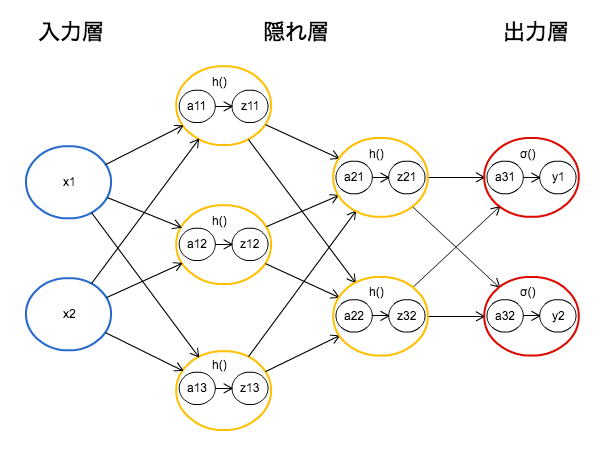
  隠れ層の活性化関数はh()で表し、出力層の活性化関数はσ()で表す。
• 行列の内積を用いることで、各ニューロンでの計算を１階層分ひとまとめに行う事ができる。

３層ニューロンネットワーク図

シグモイド関数

  h(x) = \frac{1}{1+ \mathrm{e}^{-x}}

各ニューロンの変換式

  a = w_1x_1+w_2x_2+b  

  z = h(a) 

※x:入力　w:重み　b:バイアス　a:入力信号の総和　h():活性化関数

３層ニューロンネットワークを実装する

3layered_neuralnetwork.py.py

import numpy as np
import matplotlib.pyplot as plt

# 重みとバイアスの初期化
def init_network():
    network = {}
    # 1層目
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    # 2層目
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    # 3層目
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

# 入力→出力
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # 1層目
    a1 = np.dot(x, W1) +b1  # A = XW +B
    z1 = sigmoid(a1)        # Z = h(A)
    # 2層目
    a2 = np.dot(z1, W2) +b2
    z2 = sigmoid(a2)
    # 3層目
    a3 = np.dot(z2, W3) +b3
    y = identity_function(a3)   # 最後の層のみ活性化関数が異なる

    return y

# シグモイド関数(活性化関数)
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 恒等関数(活性化関数)
def identity_function(x):
    return x

# 以下動作確認
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.31682708  0.69627909]