RubyとPythonで求めてみたのでRでもやってみる。
解き方
標本空間S={1, 2, 3, ..., 98, 99, 100}として、3の倍数であることを事象A、5の倍数であることを事象Bとすると、求める確率は：
\frac{n(A \cup B) - n(B)}{n(S)}
Rで書く
和集合はunion(x,y)で計算可能。積集合はintersect。
seq(a, b, l)でa〜bの公差lの等差数列が作成できる。
> a <- c(seq(3,100,3))
> a
[1] 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75
[26] 78 81 84 87 90 93 96 99
> b <- c(seq(5,100,5))
> b
[1] 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95
[20] 100
> e1 <- union(a,b)
> e1
[1] 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57
[20] 60 63 66 69 72 75 78 81 84 87 90 93 96 99 5 10 20 25 35
[39] 40 50 55 65 70 80 85 95 100
> (length(e1)-length(b))/100
[1] 0.27
ベン図
ついでにRでベン図も描いてみる。
VennDiagramというパッケージをインストール。
> install.packages("VennDiagram", repos="http://cran.ism.ac.jp/")
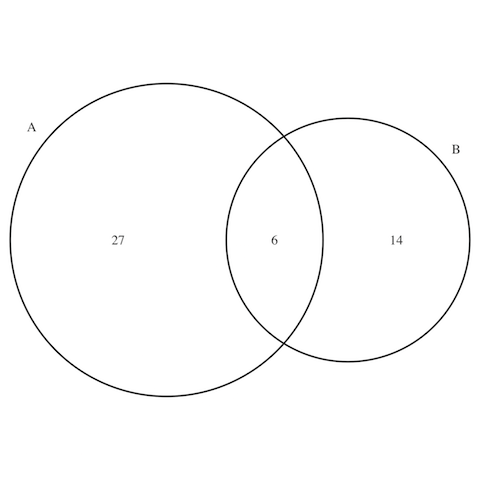
まずはシンプルにやってみる。trial.tiffというファイルに画像を保存。
> library(VennDiagram)
> venn.diagram(list(A=seq(3,100,3), B=seq(5,100,5)), filename="trial.tiff")
できた図はこんな感じ。数字は個数。
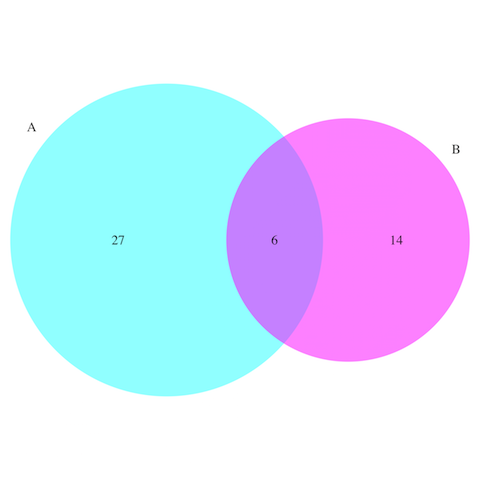
色をつけてみる。fillが塗りつぶし（5は水色、6はピンク）、ltyが縁取り線（0で線なし）、alphaは透過率です。
venn.diagram(list(A=seq(3,100,3), B=seq(5,100,5)), fill=c(5,6), lty=0, aplha=0.4, filename="trial2.tiff")
