はじめに
日本のプロ野球において、2022年の今年から「現役ドラフト」と呼ばれる選手トレードが行われます。
しかしながら、このトレードで用いられるアルゴリズムにはいくつか問題があり、現役ドラフトに参加したチームは必ずしも幸せな結果にならず、チームを強化するためには事前に他チームとトレードをする方がより良い戦略になる可能性があることに気づきました。
そこで本記事では、現役ドラフトアルゴリズムの問題点ならびに、これらの問題を解決した新たなアルゴリズムを提案します。さらに、そのアルゴリズムがある種のパレート最適、すなわちトレードに参加した全てのチームがwin-winかつ、これ以上のwin-winトレードが存在しないことを数学的に示します。
この新たなアルゴリズムによる現役ドラフトの参加には全く損がないことが保証され、さらにパレート最適なトレードによって各チームに最適に選手が割り振られるため、各チームはチームを強化するための戦略として最も最適な手法の1つになることが保証されます。
すなわち、現状各チームは現役ドラフトへの参加が義務付けられていますが、これを義務化する必要なく、むしろ自発的に参加したくなるようなアルゴリズムになります。
「現役ドラフト」とは
プロ野球に所属するチーム内での選手トレードを行うシステムで、各チームはそれぞれいくつかの条件を満たした自チームの選手を何人か選出し、アルゴリズムによってそれらの選手を入れ替えます。
2022年の場合は「2名以上選出し、1名以上獲得する」というルールがありますが、個人的にはこのルールの必要性には議論の余地があると思います。なぜならば、特に「1名以上獲得する」というルールは最初から全てにおいて最強チームである等、全くトレードしない方がチームにとって得である場合が存在するためです。
すなわち、このルールの存在自体が現役ドラフトで損をする可能性があるという問題点の一つであると考えられます。
また、「2名以上選出する」というのは現状のアルゴリズムを用いるために必要な条件であることが理由であると考えられ、一般的にはトレードに参加しないという選択肢を残す上で必要ないものであると考えられます。
実はこのルールがなかったとしても現役ドラフトに参加することでチームが損をする可能性があります。そこで、このルールは無視し全くトレードしないという選択肢を残したまま議論を進めていくことにします。
「現役ドラフト」のアルゴリズム
現役ドラフトのアルゴリズムは以下のようなものです。
(Qiitaの数式モードの仕様なのか、変なところに改行が入って読みづらい箇所がございますがご了承ください)
準備
- チームの有限集合$T$
- 選手の有限集合$M$
- 各選手の元々の所属チームを表す関数$f:M \to T$
入力
各チーム$t$は
欲しい選手の優先順位を表した全順序 $\leq_t : M \to M \to 2$1を用意し、これを入力とする。
この全順序ですが、チーム$t$にとって、選手xを選手yよりも優先して欲しい場合、`
x $\leq_t$ yと表現しているとします。
もっと単純に言うと、欲しい選手の優先順位を1位から順に割り振っていった時の順位の数字を比較するような順序になります。
ここで、本来ならば自チームの選手を選出してはいけないのですが「ある順位より下の選手を選択するくらいなら自チームの選手を残して撤退する」という選択肢を明確化するために、自チームの選手とも比較できるように定義しています。
また、実際には全順序関係を用意するのではなく、その場で適宜決めていくものだと思われますが、本記事では分かりやすさのため順序関係にしています。
出力
関数$M \to T$。すなわち選出された全ての選手の新たな所属チーム先を返す関数。
アルゴリズム
2022年における現役ドラフトのアルゴリズムは以下の通りです。
実は1人目の選出と2人目以降の選出ではアルゴリズムが異なります(これが「2名以上選出する」というルールの主な理由だと思われます)
本記事ではこの1人目の選出方法に着目して議論します。
1人目の選出方法
まず未選択のチーム$S$を全ての参加チームとし、獲得前の選手の集合$X$を全ての選手$M$として①を実行する。
①
入力
- チームの有限集合$S$
- 選手の有限集合$X$
$S$か$X$が空である場合、アルゴリズムを終了する。
どちらも空でない場合、$S$の各チーム$t \in S$の全順序$\leq_t$における最大値の選手が所属しているチームを集計し、最も指名された選手が所属する人数が多いチーム
t_0 \in \arg\max_{t \in S}\{|g^{-1}(t)|\}
ただし、$g : S \to S$を$g(s)=f(\min_{\leq_s}X)$で定義する
を1つ決める(あくまで$\arg\max$であるため、一般には一意に定まらない)
例えば、A,B,C,Dの4チームあり、それぞれのリストの先頭がB,C,B,Aチーム所属の選手だった場合はBチームが最も多い2チームから指名を受けているので$t_0:=$Bとなる。
$t_0$が決まったら、あとは$S$, $X$, $t_0$に対して②を実行する。
②
入力
- 未選択のチームの集合$S$
- 獲得前の選手の集合$X$
- 指名するチーム$t \in T$
$t$チームはそのチームの優先順位の$X$における最小値$x_0:=\min_{\leq_t}X$、つまり最も欲しい選手を獲得し、$X$から当該選手$x_0$および$x_0$の元々のチームに所属する選手全てを削除し、それを$X':=\{x \in X \mid f(x) \neq f(x_0)\}$とする。(1度選出されたチームが1巡目で複数回選択されないようにするため)
また、$S$から$t$を削除したものを$S' := S\,\backslash\,\{t\}$とする。
次に選択するチーム$t':=f(x_0)$を今獲得した選手が元々所属していたチームとする。
- $t' \notin S'$の場合、$t'$はすでに1人目を選択済みのため、まだ選択していないチーム$S'$のみに対して$X'$とともに①を実行する。
- $t'\in S'$の場合、$S', X', t'$とともに②を実行する。
式で表すとわかりづらいですが、先ほどの例で言うと、選択権のあるチームBが最も欲しいチームCの選手を獲得し、その選手の元々の所属チームCの選手を候補リストから全て削除し、今削除した選手の所属チームCに選択権が移ります。(後述の"アルゴリズムの問題点"にある例もご覧ください)
このアルゴリズムの停止性は選手の集合の減少性から言えます。
これによって、各チーム1人づつ獲得し、さらに各チームが1人ずつ選手が放出することが保証できます。
2人目以降の選出方法
1人目で選出したチームの順番によって、通常のドラフト会議と同様に逆ウェーバー制で選出していきます。本記事では深く触れません。
アルゴリズムの問題点
この1人目を選出するアルゴリズムにはトレードによって損する可能性がある場合があります。
例えば以下のような場合です。
参加チームが損する可能性1
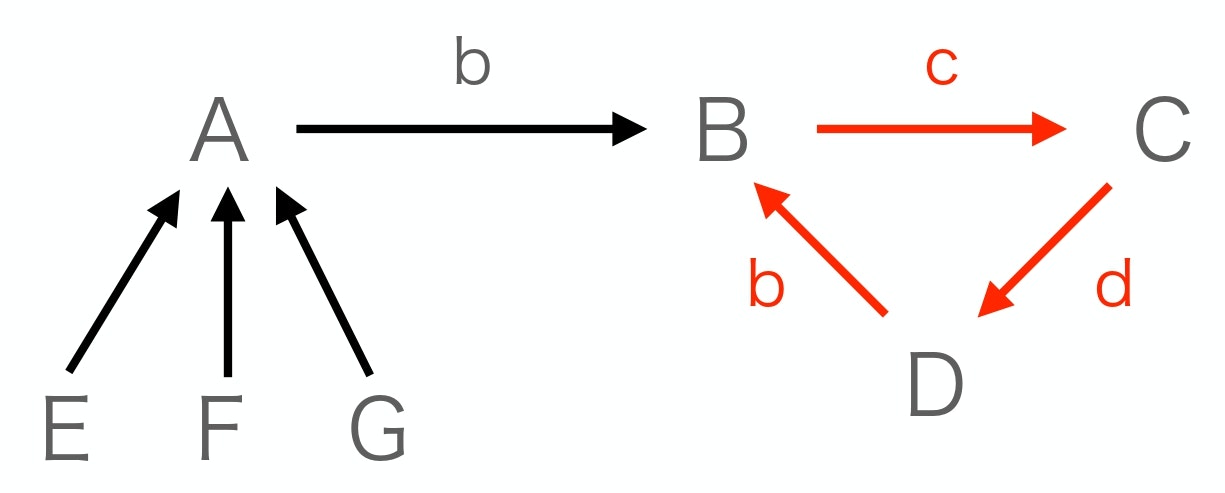
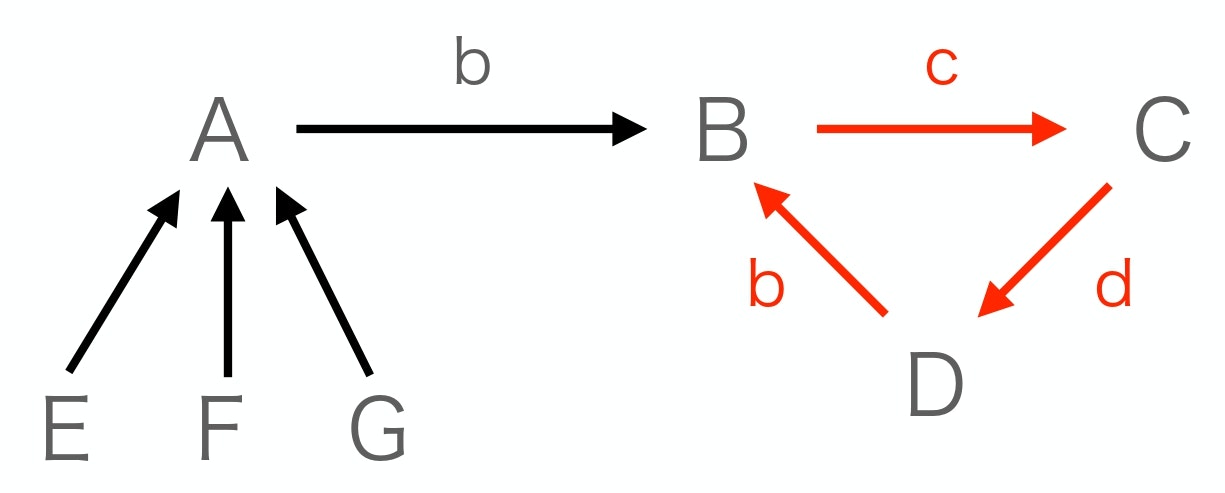
チームA, B, C, D, E, F, Gがあったとし、それぞれのチームから選出された選手がチームAからはa、...チームGからgの一人ずつであり、
欲しい選手の優先順位が上から
A -> b,a,...
B -> c,...
C -> d,...
D -> b,d,...
E -> a,...
F -> a,...
G -> a,...
だったとする。
このとき、まず最も人気のある選手の所属するチームAから順に選出し、チームAがb、チームBがc、チームCがdの選手を獲得します。
しかしながら、チームDにとって、bの次に自チームの選手dがあり、第一希望のbが獲得できないばかりでなく、トレードに参加しなければ失うこともなかったdまで放出することになり、損をしてしまいます。
しかし、チームAは多数票を得たからそちらが優先されるべきと言う考えもあります。
ところが、たとえ多数票を得たとしても損をしてしまうケースもあるのです。
参加チームが損する可能性2
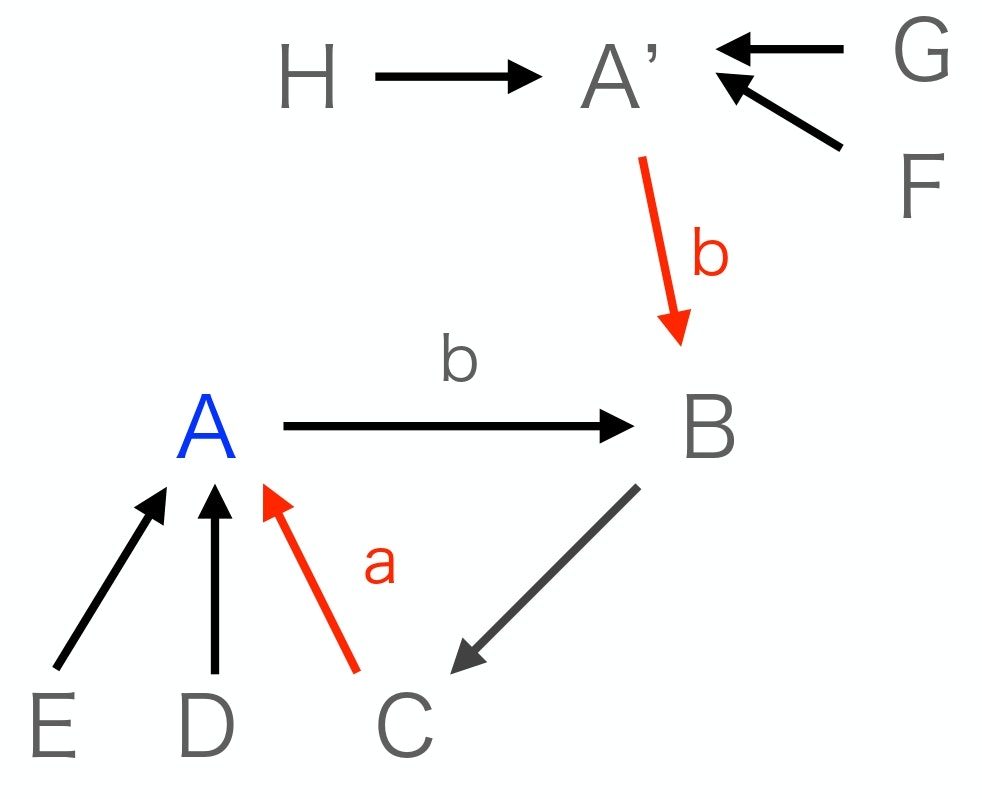
それぞれのチームの第一希望の選手が所属するチームが以下の場合を考えます。
この図のチームAとA'はそれぞれ多数票の3票を得ていて、アルゴリズムではこのうちどちらかを選んでスタートしないといけないので、A'からスタートしたとします。
ここでチームAの獲得したい選手の優先順位がb,a,...とすると、チームAは最多票タイを獲得したにも関わらず損をすることになります。
現状の現役ドラフトにおける戦略
これらの損するケースが存在することを考慮すると、各チームは現役ドラフト前にn角トレードが可能かどうかを他チームに打診するのがより良い戦略になる場合があります。
どのチームも損しないトレードは存在するのか?
先ほどの例を見ると、どこかのチームが損を被るのは仕方ないように見えますが、実はどのチームも全く損しないトレードが必ず存在します。
例えば1つ目の例では、チームBにc、チームCにd、チームDにbを三角トレードするようなwin-winトレードが存在するのでこちらを優先させ、チームAは自チームの選手aを引き取ることすればどのチームも損することはありません。
2つ目の例もA,B,C間の三角トレードを優先させることでどのチームも損をしないトレードを行うことができます。
そこで本記事で提案するのは、トレードによって参加チーム全てが損をしないことが保証されたアルゴリズムです。
「誰も損をしないトレード」とは?
まず「誰も損をしないトレード」ということが指す意味を以下で定義します。
順序集合の部分集合の比較
集合$M$上の全順序$\leq$を考える。
このとき、$M$の有限部分集合全体の集合上の順序$\leq$を以下に定める。
$X, Y \subset M$とし、$X \leq Y$を
|X| \geq |Y| \wedge 0 \leq \forall i < |Y|, x_i \leq y_i
と定義する。
ただし、
n:=|X|\\
m:=|Y|\\
\{x_0,\,\ldots,\,x_{n-1}\}=X\\
\{y_0,\,\ldots,\,y_{m-1}\}=Y\\
0 \leq \forall i < \forall j < n \Rightarrow x_i < x_j\\
0 \leq \forall i < \forall j < m \Rightarrow y_i < y_j
つまりそれぞれの要素が昇順に並んでいたとする。
例えば、X={1,4,7,9}, Y={3,5,8}であれば
これらを昇順に比較し、1 < 3, 4 < 5, 7 < 8であり、|X| > |Y|であるため、X $\leq$ Yが言える。
定義の気持ちとしては、それぞれの最も優先順位の高い選手から順に優先順位を比較していき、その全てが等しいか高くなっており、さらにチーム人数も減少していなければ「損をしていない」と判断すると言うことです。
これが半順序になることは容易に示せますが、証明は省略します。
チームが損をしないとは
これを用いてチームが損をしないことが以下に定義できます。
選手の集合$M$とし、
各チーム$t$の優先順位$\leq_t$とする。
トレード前とトレード後のチーム$t$の所属選手の集合をそれぞれ$B_t,A_t$としたとき、
チーム$t$が損をしないとは$A_t \leq_t B_t$を満たすことである。
さらに全てのチームが損をしないとは任意のチーム$t \in T$に対してチーム$t$が損をしないことである。
特に、チームが損しないためには定義より選手の人数が減ってはいけないので、トレードによって全てのチームが損しないならば、どのチームの選手の人数も元の人数と等しくなります。
次にトレード前後で全てのチームが損しないことを満たすアルゴリズムを考えます。
全てのチームがwin-winになるトレードアルゴリズム
アルゴリズムの入出力は元の現役ドラフトアルゴリズムと同様です。すなわち
入力
- チームの有限集合$T$
- 選手の有限集合$M$
- 各選手の元々の所属チームを表す関数$f:M \to T$
- 各チーム$t$の欲しい選手の優先順位を表す全順序$\leq_t : M \to M \to 2$
出力
- 選手たちが新たに所属するチームを表す関数$M \to T$
です。
アルゴリズム
アルゴリズムを簡単に説明すると、優先順位の高い順にn角トレードを探索し、それら全てを行っていくものになります。
①を選手の集合$M$を入力として実行する。
①
入力
- 選手の部分集合$X$
$X$が空ならばアルゴリズム終了
そうでなければ、各チームの最も優先順位の高い選手が所属するチームを返す関数$r:T \to T$を考える。すなわち$r(t):=f(\min_{\leq_t}X)$である。
ここで$T$が有限集合であり、$r$で定義される有向グラフによる閉路が存在するので、それを1つ取り出す。
(この閉路の探索は簡単で、適当なチームからスタートし$r$を計算して進んでいけば必ず閉路に辿り着く)
再掲するが、閉路というのは先ほどの例で言うとB,C,Dによる三角トレードである。
これらをn角トレードし、トレードした選手を$X$から取り除き、①に再帰する。
(n=1のとき、つまり自チームの選手が第一希望だった場合はその選手をそのまま引き取って自チームに戻すことを意味します)
このアルゴリズムの停止性は選手の集合$X$の減少性から言えます。
アルゴリズムの途中で"(一般に複数ある)閉路を1つ取り出す"とありますが、実は取り出す順序によらず、出力が一意に定まります。
証明は簡単で、閉路を定義するための二項関係を関数$r$で定義することから閉路がそれぞれ独立であることがわかり、最終的にトレードした選手のみ$X$から取り出すため、再帰の前後でその閉路が変化せず、それによって獲得する選手も変化しないためです。
具体例
チームA, B, C, Dがあり、選手の集合が{a1,b1,b2,c1,d1}だったとします。
そして、各選手の所属チームを
a1 -> A
b1 -> B
b2 -> B
c1 -> C
d1 -> D
とし、各チームが欲しい選手の優先順位がそれぞれ
A -> b1,b2,d1,c1,a1
B -> d1,a1,b1,c1,b2
C -> c1,a1,b2,b1,d1
D -> b1,c1,d1,b2,a1
だったとします。
このとき、このアルゴリズムの出力を見ていきます。
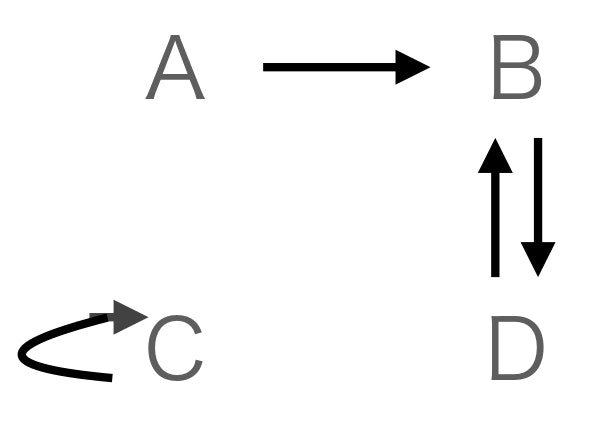
まず、各チームの優先順位の先頭を見て、その選手の所属チームに対するグラフを作ります。
このとき、B,DとCが閉路になるため、
閉路B,Dを処理し、Bが欲しい選手d1とDが欲しい選手b1をトレードします。
閉路Cのように1チームによる閉路の場合は、チームCが欲しい選手c1はトレードせずにそのまま自チームに戻すことを意味します。
その後、選手の集合から今トレードした選手b1,d1,c1を削除し、{a1,b2}とします。
すなわち残っている選手で各チームが欲しい選手の優先順位は
A -> b2,a1
B -> a1,b2
C -> a1,b2
D -> a1,b2
となります。
上と同様のことを行うと、A,Bが閉路になるので、チームAに選手b2、チームBに選手a1をトレードします。
これで全ての選手の移籍先が決まるのでアルゴリズム終了です。
出力は
a1 -> B
b1 -> D
b2 -> A
c1 -> C
d1 -> B
となります。
このとき、各チームに所属している選手の優先順位がそれぞれ
チームAは{5}から{2}に
チームBは{3,5}から{1,2}に
チームCは{1}から{1}に
チームDは{3}から{1}になり、各チームは損をしていません。
この例のように、本記事で紹介するアルゴリズムは以下のような性質が成り立ちます。
損しないトレードであるということ
これがどのチームも損しないトレードになることは、このアルゴリズムで行われるトレード全てがn角トレードであり、それらは全てwin-winトレードの場合に限ることから示せます。
ここで注意が必要なのは、どのチームも損しないトレードと言う条件を満たすだけなら、全く何もトレードしないようなアルゴリズムでも成り立つということです。
すなわち、現役ドラフトが満たすべき条件としてはこれだけでは弱いということを意味します。
しかしながら、このアルゴリズムによるトレードはさらにパレート最適、すなわちこれ以上のwin-winトレードが存在せず、これ以上どのチームも他チームを損させることなく選手を移籍させるのが不可能であるという性質も成り立ちます。
この性質こそがこのアルゴリズムによるトレードに参加する意義の1つになります。
パレート最適性
パレート最適性、つまり、これ以上どのチームも他チームを損させることなく選手を移籍するのが不可能であるという性質を示します。
まず、各チームが損をないことの定義から各チームの選手の人数が増減してはいけないので、選手が移籍するにはトレードを行うしかないということがわかります。
そこで背理法を用いて、このアルゴリズムによるトレードを行った後に更なるwin-winトレードが存在していたと仮定します。
そのトレードに属する選手のうち、元のアルゴリズムによって最初にトレードされた選手1人に着目すると、その選手はその時点で各チームの最も優先順位の高い選手によるwin-winトレードが行われていたはずです。
この時点で更なるwin-winトレードするための選手が全員残っている状態なので、アルゴリズムによって行われたトレード以外にも該当選手を含む優先順位の最も高いトレードが存在していたことになります。しかしながらこれは閉路が全て独立であることに矛盾します。
よって、更なるwin-winトレードは存在せず、パレート最適性が成り立ちます。
結論
これらの性質から、各チームがチームを強化するためには、この提案したアルゴリズムの現役ドラフトに参加することが最も効果的な戦略の1つであることがわかります。
まとめ
2022年のプロ野球における現役ドラフトのアルゴリズムにおいて、現状では現役ドラフトに参加することでむしろチームが損する可能性があり、現役ドラフトに参加する前にトレードを打診することがより良い戦略である場合が存在します。
しかしながら、本記事で提案したアルゴリズムを用いることで、全く損することなく各チームwin-winの関係になり、さらにパレート最適性によりこれ以上のトレードを行う必要がなくなる(必ずどこかのチームがloseになるようなトレードしか存在しない)という性質を保証することができ、提案した手法の現役ドラフトに参加するだけで最適なチームを作ることができるようになります。
-
集合$2 := \{\top,\bot\}$. すなわち真偽値の集合とする。 ↩