線形回帰モデル
y = aw+bの式で表示できるものであって直線にて表現できるものの事を線形回帰モデルという。
また、aを回帰係数、bをバイアスという。
さらに線形回帰モデルには、重回帰分析などがある。
線形回帰は、未知の値を予測するために実際のデータを使い、値が取ると予想される数値を求める。また、実値と回帰式の差を残差といい、この残差を最小化する事を目的として計算される。(損失関数の最小化)
この際に、しばしば最小2乗法を利用し損失関数の最小化を計算する。
計算式は、sum((x-x.mean())**2)/n にて求める事が可能。(nはデータ個数)
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
import pandas as pd
import matplotlib.pyplot as plt
# ボストン住宅価格をダウンロード
boston = load_boston()
# 単回帰分析(説明変数が13カラムある中、5番目を参照)
x = boston.data[:, 5]
y = boston.target
# 線形回帰
linear = LinearRegression()
linear.fit(x.reshape(-1,1),y.reshape(-1,1))
# 図
plt.scatter(x, y, color='lightblue')
plt.plot(x, linear.predict(x.reshape(-1,1))) # y = ax+b
plt.show()
# 下記のplotが誤差(x-x.mean())に対して最適な回帰直線になる。
# 線形回帰は損失を計算する場合など様々なケースで利用されているので必須事項である。
非線形回帰モデル
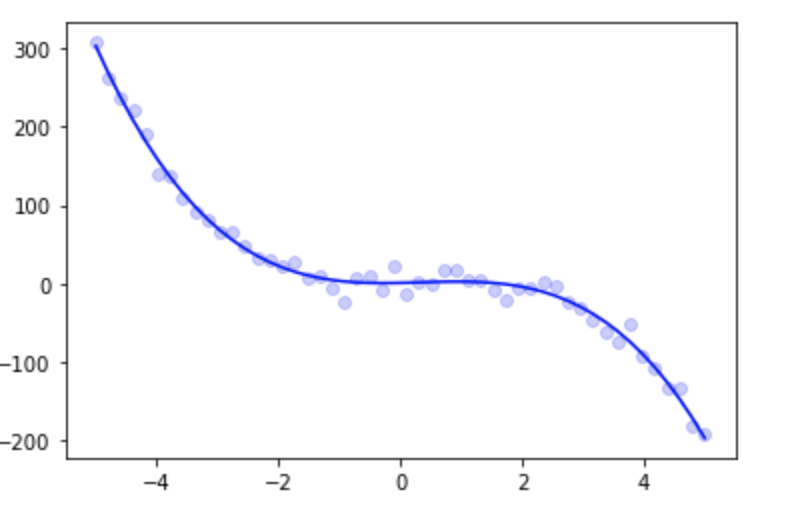
上記の線形回帰だけでは表現できないモデルのことを言うが、直線ではなく曲線によって表現されるモデルを非線形回帰モデルという。
多項式関数などが良い例である。(wx1+wx2*wx**3...)
非線形回帰では、ペナルティーという概念があり、異常値など分布が逸脱してしまった際にペナルティーを課さないと過学習が起こりやすい(数値に上限を設けないため)
ペナルティーを課した非線形回帰モデルとしてはラッソ回帰や、リッジ回帰などがある。
ラッソ回帰では、L1ノルムのペナルティーを課しており、ユーグリット距離を元に計算している。また、スパースな解を求める事が可能
リッジ回帰では、L2ノルムのペナルティーを課しており、マンハッタン距離を元に計算している。
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
x = np.linspace(-5, 5, 50).reshape(-1,1)
y = 2 * x + 2 * x ** 2 - 2 * x ** 3 + np.random.normal(scale=10, size=x.shape)
np.random.seed(0)
pf = PolynomialFeatures(degree=3, include_bias=False)
lr = LinearRegression()
pl = Pipeline([("PF", pf), ("LR", lr)])
pl.fit(x, y)
pred_y = pl.predict(x)
plt.scatter(x, y, c="b", alpha=0.2)
plt.plot(x, pred_y, c="b")
ロジスティック回帰モデル
ロジスティック回帰とは分類問題を解くタスクで特に2値分類を実施する際に利用する。
0~1の数値が出力され、閾値を0.5に設定する事で分類が可能。
式は1/(1+exp(-x))にて計算される。
また、xには、wx+bの回帰式が当てはまる。(勿論重回帰分析の式も可能)
ただし、昨今ではlightgbmなど強力なモデルの登場により、あまり見られないケースが多い。
上記のGBDT系モデルはデータ量が大量に必要なため、データ量があまり確保できない状況で利用する。
from sklearn.linear_model import LogisticRegression
fx_train, x_test, y_train, y_test = train_test_split(x,y)rom sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd
import matplotlib.pyplot as plt
iris = load_iris()
x = iris.data[:100]
y = iris.target[:100]
# ロジスティック回帰の実装
model =LogisticRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test) # ラベルを予測
pred_proba = model.predict_proba(x_test) # 確率を予測
print(f'2値分類の予測ラベルは{pred}')
print('-'*50)
print(f'2値分類の予測確率は{pred_proba}') # [0,1]の順番でクラスの確率が表示される
print('-'*50)
print(model.score(x_test, y_test)) # accuracyが今回は100%
'''
2値分類の予測ラベルは[0 1 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 1]
--------------------------------------------------
2値分類の予測確率は[[0.96911637 0.03088363]
[0.05450741 0.94549259]
[0.00440392 0.99559608]
[0.97163851 0.02836149]
[0.96443406 0.03556594]
[0.002139 0.997861 ]
[0.01260641 0.98739359]
[0.0741632 0.9258368 ]
[0.98042462 0.01957538]
[0.00626669 0.99373331]
[0.02352094 0.97647906]
[0.98223986 0.01776014]
[0.15088556 0.84911444]
[0.02562067 0.97437933]
[0.96442573 0.03557427]
[0.98499644 0.01500356]
[0.97152184 0.02847816]
[0.98416773 0.01583227]
[0.00479668 0.99520332]
[0.00947793 0.99052207]
[0.98980729 0.01019271]
[0.03736068 0.96263932]
[0.01129443 0.98870557]
[0.94429826 0.05570174]
[0.00273282 0.99726718]]
1.0
'''
主成分分析
次元削減に利用される。
次元を分散が最大になる形で圧縮するもの(情報の損失を避けるため)
圧縮したものを主成分といい、第1主成分、第2主成分...のように存在する。
これらの主成分が元の情報をどれだけ持っているのかを示したものを寄与率といい、80%以上維持できるように調整するのが好ましい。
基本的な利用方法だが、可視化やクラスタリングを併用して使う事が多く、情報を圧縮したもののため、新たな特徴量としてモデリングの際にはあまり利用しない。
from sklearn.decomposition import PCA
iris = load_iris()
x = pd.DataFrame(iris.data, columns=iris.feature_names)
# PCA
pca = PCA(n_components=2)
pca_data= pca.fit_transform(x)
print(pca.explained_variance_ratio_) # 寄与率92%
# 可視化のためdataFrameに合併
x['pca1'] = pca_data[:, 0]
x['pca2'] = pca_data[:, 1]
x['target'] = iris.target
target = np.unique(iris.target)
# 可視化
for label in range(3):
plt.scatter(x[x['target'] == label]['pca1'], x[x['target'] == label]['pca2'], label=label)
plt.legend()
plt.show()
# 圧縮した情報はラベルで表現可能。
# PCAでは圧縮した情報を元にクラス情報を投入する事で傾向を使うときに利用する
# 例:法人と個人のラベルを投入して法人にはない個人の動きや、個人にはない法人の動きなどを把握する
アルゴリズム
k-近傍法とは、教師あり学習で、特定の点から近い順にk個を選択するもの。
選択したk個の中でクラスの多数決を行い最も多いクラスが特定の点のクラスになる。
kは3~5にて行われる事が多い。kが多すぎたり小さすぎたりすると偏った結果になりがちである。
ちなみに分類問題である。
k-meansとは、教師なし学習で、分割するクラスの個数を決定し、自動でクラスターにい分類する手法。
分割する分布の点情報をまずはランダムにk個選択する。
そしてランダムに分布されている点をk個選択する。
選択されたk個の点から各点の距離を求め、最も距離が小さかったランダムに選択されたk個のクラスに所属する。
所属したクラスの中で、重心を求める。
重心起点に、再度距離を求めてクラスターを分割する。(重心の変化がなくなるまで実施する)
from sklearn.cluster import KMeans
iris = load_iris()
x = pd.DataFrame(iris.data, columns=iris.feature_names)
y = pd.DataFrame(iris.target, columns=['target'])
kmeans= KMeans(n_clusters=3)
cluster = kmeans.fit_transform(x.loc[:, ['sepal length (cm)', 'sepal width (cm)']])
classes = kmeans.predict(x.loc[:, ['sepal length (cm)', 'sepal width (cm)']])
x['classes'] = classes
label = [0,1,2]
# クラスターのクラス
for i in range(3):
plt.scatter(x[x['classes']==i]['sepal length (cm)'], x[x['classes'] == i]['sepal width (cm)'], label=label[i])
plt.legend()
plt.show()
サポートベクトルマシーン
サポートベクトルマシンは、分類問題に利用する。
線形、非線形両方に対応している。
考え方として、分類問題のため、各クラスから境界線が遠いように設計するのが好ましい。
そのため、2クラス間で距離の最も近い点に対して最大化するように実施する。
また、境界線に対してハードマージン、ソフトマージンの考え方が存在し、前者は境界線に対して厳格であり、後者は境界線に対して許容範囲が存在する。
ハードマージンでは、min((1/2)||w||**2)
ソフトマージンでは、min(1/2)||w||**2 + C*sum(ξ))にて求める事が可能
線形分離できないものは、2次元で分離を検討するのではなく3次元等、面での分離を検討やり方がある。それがカーネルを利用した手法である。
from sklearn.svm import LinearSVC
iris = load_iris()
x = pd.DataFrame(iris.data, columns=iris.feature_names)
y = pd.DataFrame(iris.target, columns=['target'])
x_train, x_test, y_train, y_test = train_test_split(x,y)
# ハードマージン
svm = LinearSVC(C=np.inf)
svm.fit(x_train, y_train)
pred = svm.predict(x_test)
score = svm.score(x_test, y_test)
print(f'予測のラベル情報は{pred}')
print(f'正解率は{score}')
print('-'*50)
# --------------------------------
# ソフトマージン
svm = LinearSVC(C=1.0)
svm.fit(x_train, y_train)
pred2 = svm.predict(x_test)
score2= svm.score(x_test, y_test)
print(f'予測のラベル情報は{pred2}')
print(f'正解率は{score2}')
# 完全に分離できる場合は、ハードマージンを利用するがそうではない場合、ソフトマージンを利用する
# 正解率で見てみるとソフトマージンの方がスコアが良い結果になった。
'''
予測のラベル情報は[2 1 1 2 2 1 0 0 1 1 2 1 0 0 0 1 1 0 0 0 0 1 0 1 1 2 2 0 0 2 0 2 1 1 2 1 1
0]
正解率は0.8421052631578947
--------------------------------------------------
予測のラベル情報は[2 2 1 2 2 2 0 0 1 2 2 1 0 0 0 1 2 0 0 0 0 2 0 1 1 2 2 0 0 2 0 2 2 1 2 2 1
0]
正解率は0.9736842105263158
'''