http://scikit-learn.org/0.18/modules/random_projection.html を google翻訳した
scikit-learn 0.18 ユーザーガイド 4. データセット変換 より
4.5. ランダムプロジェクション
sklearn.random_projection モジュールは、より高速な処理時間とより小さなモデルサイズのために制御された量の精度(追加の分散として)を取引することによって、データの次元を低減する簡単で計算上効率的な方法を実装します。このモジュールは、2つのタイプの非構造化ランダム行列、ガウスランダム行列とスパースランダム行列を実装します。
ランダム投影行列の次元および分布は、データセットの任意の2つのサンプル間の対の距離を保存するように制御される。したがって、ランダム投影は、距離に基づく方法の適切な近似技法である。
- 参考文献:
- Sanjoy Dasgupta。 ランダム射影による実験 。人工知能(UAI'00)、Craig BoutilierおよびMoisésGoldszmidt(Eds。)の不確実性に関する第16回会議の議事録。 Morgan Kaufmann Publishers Inc.、San Francisco、CA、USA、143-151。
- エラ・ビンガムとヘイキ・マンニラ 2001 次元削減におけるランダム投影:画像とテキストデータへの応用 知識発見とデータマイニングに関する第7回ACM SIGKDD国際会議の講演会(KDD'01) ACM、New York、NY、USA、245-250。
4.5.1. Johnson-Lindenstraussの補題
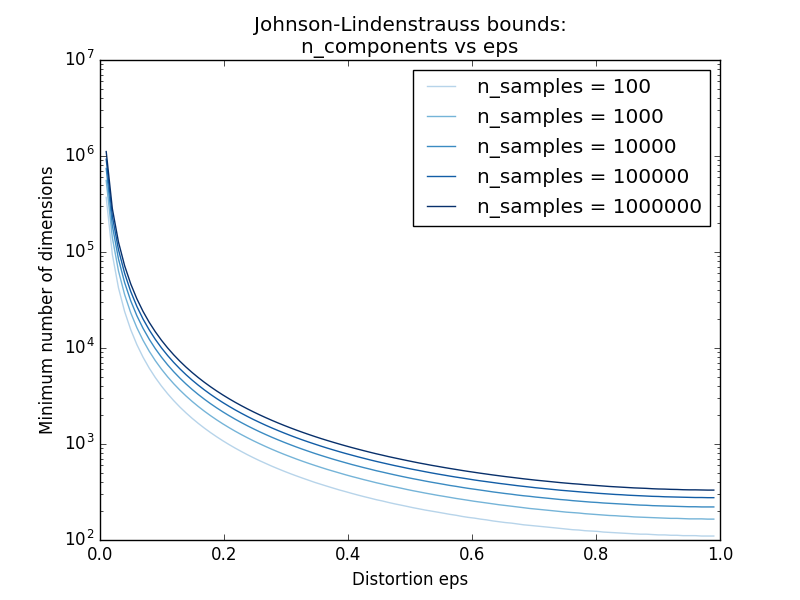
ランダム射影の効率の主な理論的結果は、 ジョンソン・リンデンシュトラウスの補題(Wikipediaを引用) です。
数学では、Johnson-Lindenstraussの補題は、高次元から低次元のユークリッド空間への点の低歪み埋め込みに関する結果である。補題は、高次元空間における小さな点集合を、点間の距離がほぼ保存されるように、はるかに低い次元の空間に埋め込むことができると述べている。埋め込みに使用されるマップは、少なくともLipschitzであり、正射影であるとみなすこともできます。
sklearn.random_projection.johnson_lindenstrauss_min_dim は、サンプル数だけを知っているので、無作為部分空間の最小サイズを控えめに推定し、ランダム投影によって導入される有界な歪みを保証します。
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
- 例:
- Johnson-Lindenstraussの補題に関する理論的解説と、疎なランダム行列を用いた経験的検証のためのランダム投影による埋め込みのためのJohnson-Lindenstrauss参照。
- 参考文献:
- Sanjoy DasguptaおよびAnupam Gupta、1999年。Johnson-Lindenstrauss補題の初歩的証拠。
4.5.2. ガウスランダム投影
sklearn.random_projection.GaussianRandomProjectionは、元の入力スペースをランダムに生成されたマトリックスに投影して次元を減らします。ここで、コンポーネントは次の分布 $N(0, \frac{1}{n_{components}})$ から引き出されます。
ここでは、ガウスランダム投影トランスフォーマーを使用する方法を示す小さな抜粋:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
4.5.3. スパースランダム投影
sklearn.random_projection.SparseRandomProjection は、スパースランダム行列を使用して元の入力空間を投影することによって次元を減らします。
スパースランダム行列は、密度の高いガウスランダム射影行列の代替であり、同様の埋め込み品質を保証し、さらにメモリ効率が高く、投影データの高速計算を可能にします。
s = 1 / density を定義すると、ランダム行列の要素は
\left\{
\begin{array}{c c l}
-\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
0 &\text{with probability} & 1 - 1 / s \\
+\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
\end{array}
\right.
ここで、 $n_{\text{components}}$ は投影された部分空間のサイズです。デフォルトでは、非ゼロ要素の密度はPing Li et alによって推奨された次の最小密度に設定されます。 $1 / \sqrt{n_{\text{features}}}$
スパースランダム投影変換を使用する方法を示す小さな抜粋:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100,10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
- 参考文献:
- D. Achlioptas データベースに優しいランダム投影法:Johnson-Lindenstraussとバイナリコイン コンピュータ・システム科学66(2003)671-687
- Ping Li、Trevor J. Hastie、およびKenneth W. Church 2006 非常にまばらなランダム投影 知識発見とデータマイニングに関する第12回ACM SIGKDD国際会議の講演会(KDD '06) ACM、New York、NY、USA、287-296。
scikit-learn 0.18 ユーザーガイド 4. データセット変換 より
©2010 - 2016、scikit-learn developers(BSDライセンス)。