高速な経路探索アルゴリズムの実装と課題

はじめに

NAVITIME JAPAN Advent Calendar 2019の19日目を担当いたします、経路探索アルゴリズムの研究開発をしているsuekiです。好きなデータ構造はセグメント木です。

本稿では弊社で導入している経路探索アルゴリズムの高速化手法とその課題について紹介します。

経路探索の高速化手法について

グラフ上における2点間の経路探索と言えばダイクストラ法¹が有名で、
弊社のサービスでも徒歩・自転車・車の経路はダイクストラ法をベースとしたアルゴリズムによって求められています。

ナイーブなダイクストラ法の計算量は $O((E+V)\log{V})$ 程度です。
しかし日本全国では数千万本のリンクが存在するため、より高速に経路探索を行うアルゴリズムが必要です。

• クエリが来る前の事前処理の有無
• 事前処理と探索時間のバランス
• 多様なコストモデルの考慮可否

などに応じた様々な手法が存在し、ナイーブなダイクストラ法では数秒かかってしまうような探索をナノ秒単位で実現できるような手法がいくつも提案されています。

全体を俯瞰したい方には
こちらの資料またはこちらの論文が詳しいです。

今回はその中でも弊社で利用実績があり、数千万頂点規模のグラフに適用可能な手法内ではクエリ時間が現状ほぼ最速の手法である hub labeling系の手法について紹介します。

hub labelingとは

ざっくり言うと、

• グラフ上の各ノードに対し、グラフ上のいくつかのノードまでの最短距離を事前計算しておく
• ノードAからノードBへの最短経路長が欲しい場合、AとBが共通で距離を知っているノード(hub)のどれかを経由するのが最短経路となる
• ↑の性質を満たすように、うまく枝刈りをしながら事前計算を行う

という手法になります。枝刈りの実行方法によって前処理の時間やデータサイズが大きく変わるため、様々な手法が提案されています^{2 3 4}。

前処理結果・クエリの具体例

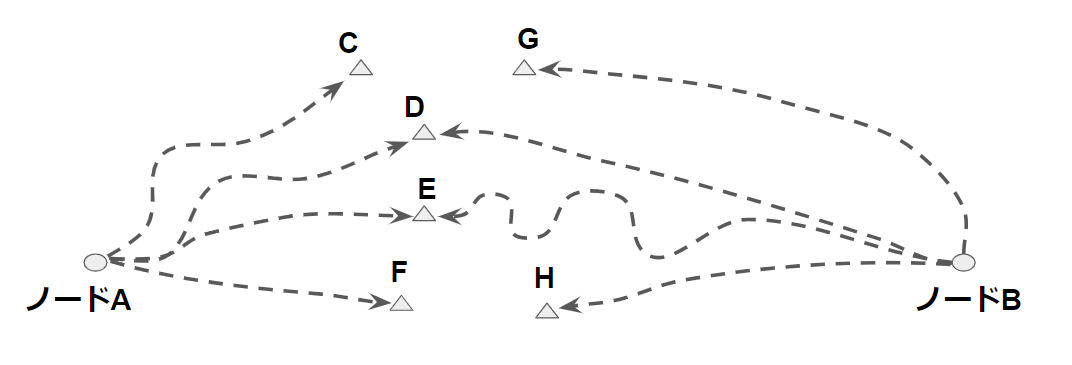
ノードAはノードC,D,E,Fまでの最短経路を知っており、ノードBはノードD,E,G,Hまでの最短経路を知っている想定です。それぞれの最短経路コストは以下の通りとします：

from	to	distance
A	C	30
A	D	20
A	E	15
A	F	25
B	D	50
B	E	100
B	G	30
B	H	10

この例ではAとBが共通で最短距離を知っているのがノードDとEになるので、

• A～D～B : 20 + 50 = 70
• A～E～B : 15 + 100 = 115

となり、AからBへの最短経路コストは両者のうち最小である70と計算されます⁵。

前処理を適切に行うことで、100万頂点/1億リンク程度の大規模なソーシャルグラフに対しても
一つのノードに対して最短距離を保存するノード数を平均で数十～数百に抑えられ、わずか1秒程度で前処理が終わることが報告されています⁴。

道路ネットワークに特化したhub labeling

上記の手法を道路ネットワーク向けにさらに拡張したものがpruned highway labeling⁶になります。

先程の手法ではノードがhubになっていましたが、こちらの手法ではパス（連続するリンク列）をhubとしており、各頂点は

• パスのID
• パス上のある地点までの距離
• パスの先頭から上述の「ある地点」までの距離

の３つを記憶します。

前処理結果・クエリの具体例

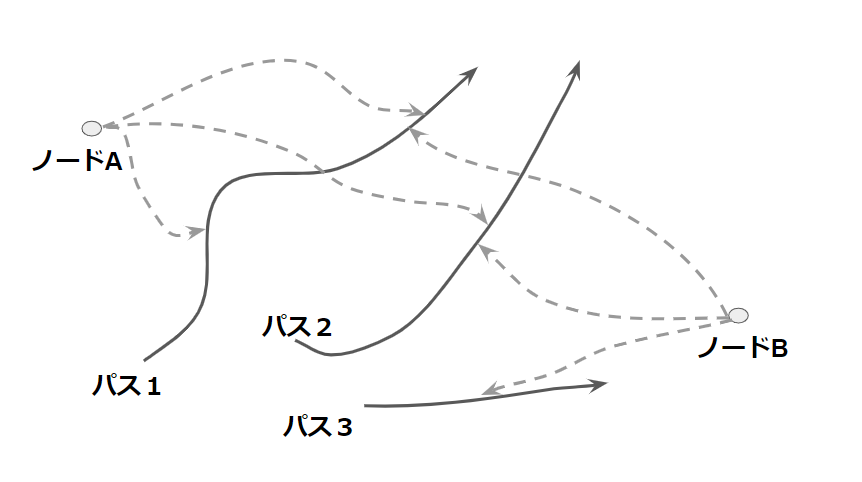
今回の例ではノードAがパス１上の２点とパス２上の１点までの距離を、
ノードBはパス1,2,3上の1点ずつまでの距離が前処理で求まっています。

それぞれの前処理結果は以下の通りとします：

ノード	パスID	パスまでの距離	パス先端からの距離
A	1	30	40
A	1	90	110
A	2	110	120
B	1	150	100
B	2	70	80
B	3	60	40

この例ではA~Bへの経路は

• パス1を介する経路
  • 30 + (100 - 40) + 150 = 240
  • 90 + (110-100) + 150 = 250
• パス2を介する経路
  • 110 + (120-100) + 70 = 200

の3通りが考えられ、最小コスト200が得られます。

なぜhubをパスに拡張したのか

ソーシャルグラフには次数（ノードから出るリンクの数）が非常に高いノードが多数存在して多くのノードのハブとして機能していることが知られています。

一方で道路ネットワークのノード次数は高々10程度のため、「▲■交差点」などといった単一のノードよりも「XX高速道路」などといったパスのほうがハブとしてより適切だと考えられます。
例えば関東から関西に行く場合、ほとんどの最短経路は東名高速や中央道など一部の高速道路を通ることになると思われます。

実際にノードをhubとした手法よりも前処理時間・前処理データサイズの両面が大きく改善されたことが論文により示されています⁷。

アルゴリズムの適用結果

上記のアルゴリズムはなんと論文著者の方がgithubに実装を公開してくださっているため、
適用したいグラフを所定の形式で用意すれば簡単に試すことができます。kawateaさんありがとうございます！⁸

ただしこのアルゴリズムは前処理結果をすべてメモリ上に乗せて動作するため、大規模なネットワークデータを扱う際にはそれなりのメモリ容量を持ったマシンが必要になります⁹。

以下に当社で利用している徒歩 / 自転車 / 自動車向けネットワークに対し、所要時間をコストとしてこのアルゴリズムで前処理を行った結果についてまとめました。

	ノード数	リンク数	前処理時間[sec]	前処理結果データサイズ	平均クエリ時間[us]	参考:ダイクストラ法のクエリ時間[us]
徒歩	約1571万	約2229万	5,087	約26GB	1.9	1,790,465
自転車	約1299万	約1830万	2,092	約16GB	2.0	1,548,881
自動車	約1088万	約1453万	983	約9GB	1.7	1,476,990

見ての通り、単純なダイクストラ法では1秒以上かかるような経路探索がわずか2マイクロ秒程度で完了することがわかりました¹⁰。

徒歩ネットワークは駅や商業施設内の細かいリンクが多く存在するためノード数やリンク数が増えており、それが処理時間や前処理結果データサイズにも影響しています。

ですがそれ以上に大きく影響したのはhighway的な道路の存在でした。
今回は自動車の速度を高速道路では時速80km、国道県道では40km、裏道では15kmなどとして簡易的に所要時間を試算した¹¹のですが、徒歩では裏道も大通りも時速にほとんど差が無いためハブとなる（＝多くの最短経路に含まれる）道路が少なくなり、枝刈り効率が下がったものと考えられます。
実際に徒歩で裏道の速度をそのままに大通りの速度を時速20kmとしたところ、同じグラフで前処理が40%速くなりました。

より現実問題に即した課題設定

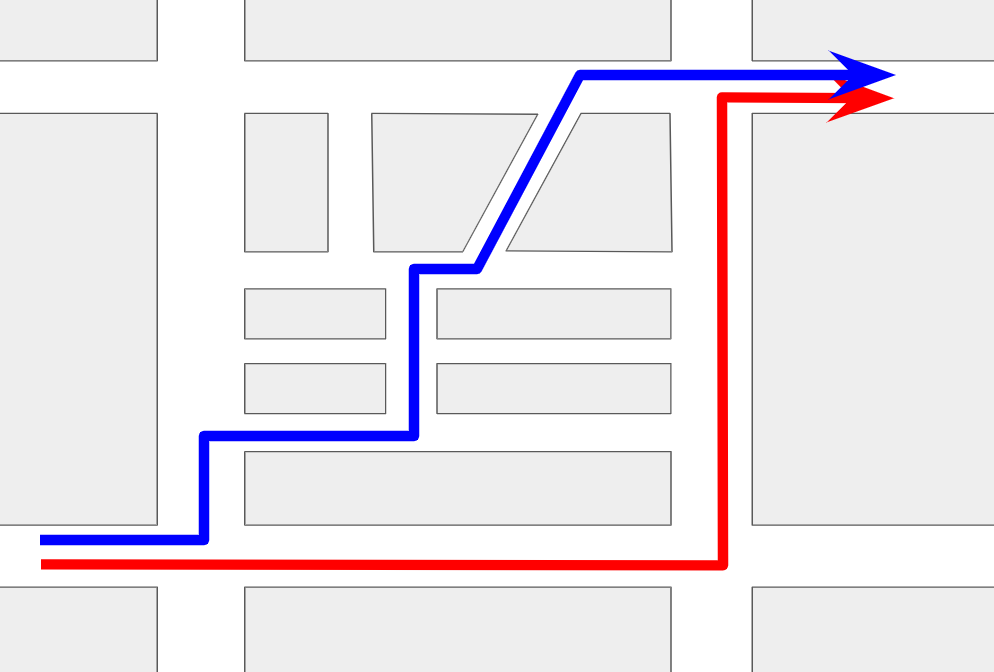
突然ですが、あなたが自動車を運転しているとしたら以下の図で赤と青の経路のどちらを通りたいでしょうか。

距離は青のルートの方がわずかに短いのですが、多くの方が赤いルートの方を選ぶのではないかと思います。
（勝手知ったる地元の道で大通りの信号待ちを避けたい、といった特殊な状況はここでは考えないことにします）

一般的に慣れない場所であれば右左折の回数はなるべく減らして分かりやすいルートを走行したいのではないかと思います。
このようなケースに対応するには、1つ前のリンクからどの方向に進んだかによってコストを変化させる必要があります。

今まで扱っていたグラフではリンク単位でコストを割り振っていたため、このように複数のリンクにまたがって表現されるコストは現状のグラフ構造では考慮できていませんでした。
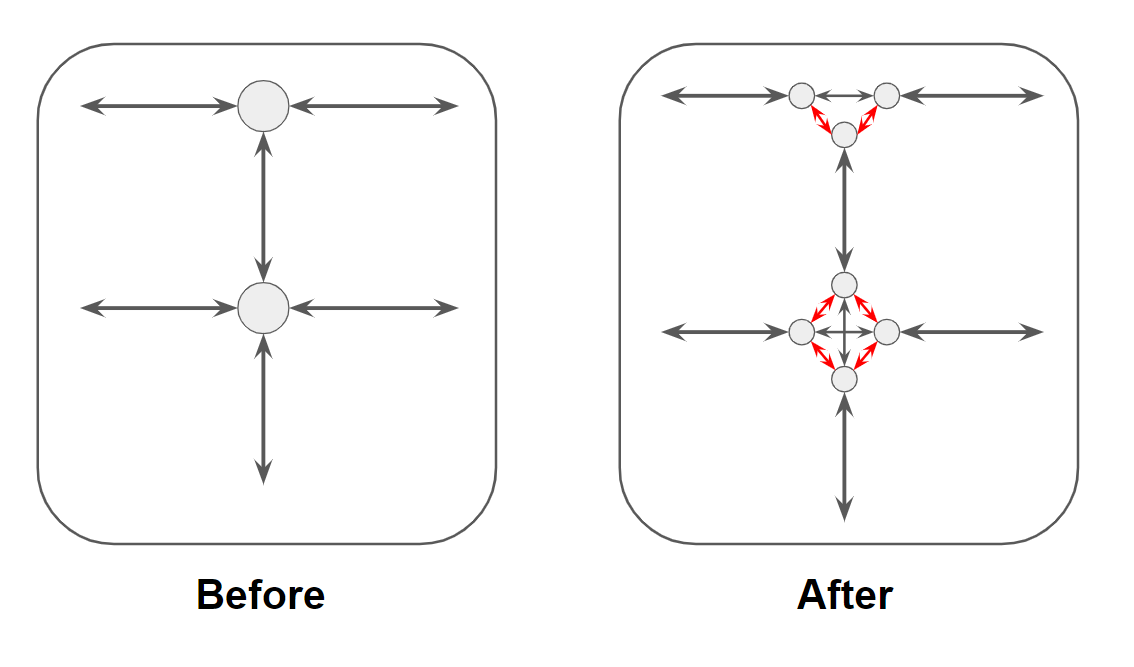
そこで以下のようなグラフの変換を考えます。

交差点ノードを進行方向ごとのノードに分割し、進行方向ごとにリンクを張り直しています。右左折にペナルティのコストを掛けたければ、Afterのグラフ上の赤いリンクにそのコストを掛ければよいです。
この変換によって複数のリンクにまたがっていた右左折のコストを一本のリンクにかかるコストとして表現することができます。

拡張したグラフに対するアルゴリズムの適用結果

上記の拡張を加えたグラフに対して、先程と同様にpruned highway labelingを行ってみました。

	ノード数	リンク数	前処理時間[sec]	前処理結果データサイズ	平均クエリ時間[us]	参考:ダイクストラ法のクエリ時間[us]
徒歩	約3788万	約9024万	16,835	約91GB	2.1	5,284,721
自転車	約3349万	約8189万	10,396	約62GB	1.9	4,970,529
自動車	約2765万	約6533万	4,568	約34GB	1.8	5,024,015

まずグラフの拡張によってリンク・ノード数が3～4倍程度増えています。

ダイクストラ法はリンク数増の影響をもろに受けてクエリ時間が大きくなってしまいましたが、pruned highway labelingのほうはその影響は薄く依然として数マイクロ秒での高速な探索が実現できています。

一方で前処理時間やデータサイズについてはグラフ拡張の影響を大きく受けており、どのケースでも4倍程度になってしまいました。ノード・リンク数以外にhighway的な道路の存在有無がデータサイズ等に影響しているのもグラフ拡張前と同様の傾向と思われます。

アルゴリズムの課題

高速道路に類する道路が存在しない道路ネットワークでの処理効率低下

計測結果の紹介時にも触れましたが、道路ごとの大きな速度変化が無い道路ネットワークでは枝刈りの効率が悪化してしまいます。

それでも橋やトンネルなど地形上ハブのような役目を果たしやすい道路は存在すると考えられるため、そのあたりの性質を活用できないかと考えています。

有向グラフへの拡張の難しさ

これまで見てきたアルゴリズムはすべて無向グラフ上での処理として紹介してきましたが、これらのアルゴリズムは有向グラフへの拡張が可能です。
各ノードに対して

• 自分自身を出発地としたときの、目的地ノードとその最短距離
• 自分自身を目的地としたときの、出発地ノードとその最短距離

の2方向の前処理結果を保持しておくことで、無向グラフの場合とほぼ同等の高速な最短経路クエリが実現できます。

しかし有向グラフになることで（特にpruned highway labelingでは）枝刈り効率が急激に下がってしまい、前処理時間が無向グラフ版の数十倍となってしまいます¹²。またそれに応じて前処理データのサイズも激増してしまいます。

一方通行があるとはいえ大部分の道路は両側通行なので、無向グラフにちょっと毛が生えたような有向グラフだと思って同様の処理ができるのではと思われるかもしれません。しかし上り線や下り線片方の入り口のみがあるハーフインターをはじめとして現実の道路ネットワークには様々な要素が含まれているため、そのような近似はあまり現実的ではないと考えています。

リアルタイム情報が考慮できない

これらのアルゴリズムは前処理時に各リンクのコストが定まっていることを前提としているので、事故や渋滞などリアルタイムに発生する情報を考慮することができません。

これは前処理系の手法である以上仕方がないことなのですが、応用先を考える時の制限事項として頭に入れておく必要があります。

まとめ

ここまで見てきた通り、hub labeling系の手法は非常に高速な最短経路クエリを実現するものの、経路品質を高めるために各種要素を盛り込むと前処理時間やデータサイズが肥大化してしまうのが現状です。
そのため現在は経路品質上の制限事項を許容できる一部のユースケースに対してのみ利用しています。

有向グラフ上での最短経路クエリが高速に実行できれば、たとえば自動車の巡回経路探索において各地点間の所要時間を求める計算が大幅に高速化できる¹³ため、
今後は関連研究¹²などを参考にしつつ有向グラフでも高速に動作するpruned highway labelingの拡張について検討を行っていきたいと考えています。

---

1. ダイクストラ法 - Wikipedia, 元論文 ↩

2. A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks ↩

3. Hierarchical hub labelings for shortest paths ↩

4. 2-Hop ラベルの直接的な計算によるグラフ最短経路クエリ処理の効率化 ↩

5. ノードへの距離だけでなく、その最短経路における自身の１つ先のノードを前処理データとして保持することで最短経路長だけでなく最短経路自体の復元が可能になります ↩

6. Fast shortest-path distance queries on road networks by pruned highway labeling ↩

7. クエリ時間は微増しますが、元々数百nsのクエリ時間が数倍になる程度の影響です ↩

8. 論文では細かく言及されない実装上の細かいコツなどもコードに詰まっているため、非常に参考になりました ↩

9. 上記論文では著者らはメモリ288GBのマシンを使っていました。 ↩

10. ダイクストラ法には一切の高速化を入れていないので、前処理なしでも双方向探索化・直線距離ベースのA*コスト導入などで最適性を損なわずにもう数倍程度は高速化の余地があります ↩

11. 実際のカーナビアプリでは渋滞等も考慮してより詳細な所要時間推定を行っています ↩

12. 有向道路ネットワーク向け最短路クエリのための効率的枝刈り探索手法 ↩

13. 無向グラフでは一方通行の逆走を前提とした所要時間が計算されてしまい、巡回経路の品質が落ちてしまいました ↩