はじめに
こんにちは.東京大学理学部物理学科B2の灰陶です.Phisics Lab. では統計物理班と数理物理班に参加しています.
本記事は,東京大学理学部物理学科の有志による 理物 Advent Calender 2022 の17日目の記事です.
本記事では,プログラミング言語 Julia について紹介し,Julia を用いて 2次元 Ising モデルのシミュレーションを行ってみます.
What is Julia?
Julia は科学技術計算向けの言語として開発されました.2018年に安定版のバージョン1がリリースされたばかりの,まだまだ成長途中の言語です.
Julia には,以下のような特徴があります.
- Python のように平易な文法
- 動的型付け言語でありながら,C や Fortran などの静的型付け言語に迫る計算速度
- MATLAB と同等の線型代数計算の記述
- Unicode 文字対応に起因する高い可読性
これらの特徴についての詳しい説明はここでは避けます.詳しく知りたいという方は,文献1を読んでみてください.
シミュレーション概要
シミュレーションに必要な Ising モデルの知識とシミュレーションの方法について説明します.
Ising モデルミニマム
格子状の2次元 Ising モデルの Hamiltonian は次式で与えられます:
$$
H = -J\sum_{\langle i,~j\rangle} \sigma_{i}\sigma_{j} - h\sum_{i}\sigma_{i}.
$$
第1項はスピン間相互作用を表しており,その和は互いに隣り合う全てのスピンの組 $i,~j$ についてとるものとします.各 $\sigma_{i}$ は $\pm1$ のいずれかの値をとり,$+1$ は外部磁場と同じ向きのスピンを,$-1$ は外部磁場と逆向きのスピンを表します.定数 $J$ は交換相互作用定数といい,$J>0$ で強磁性の,$J<0$ で反磁性体の相互作用を記述します.第2項は外部磁場とスピンの間の相互作用を表しています.定数 $h$ は電子の磁気モーメントと外部磁場の積です.
ここで,第1項の和は次のように書き換えられます:
$$
\sum_{\langle i,~j\rangle} \sigma_{i}\sigma_{j} = \sum_{\langle i,~j\rangle} \frac{\sigma_{i}\sigma_{j}+\sigma_{j}\sigma_{i}}{2} = \frac{1}{2}\sum_{i}\sigma_{i}\sum_{j_i}\sigma_{j_i}.
$$
$j_i$ についての和は $\sigma_{i}$ に隣接するスピンについてとり,$i$ についての和はすべてのスピンについてとります.前者の和を $S_i$ と置くことで,Hamiltonian の次の表式を得ます:
$$
H = -\sum_{i}\left(\frac{J}{2}\sigma_{i}S_{i} + h\sigma_{i}\right).
$$
この表式はシミュレーションコードを書く際に用います.
外部磁場のない($h=0$)2次元 Ising モデルについては厳密解が見つかっています.それによると,2次元 Ising モデルでは,
$$
\frac{k_\text{B}T_{\text{C}}}{J} = \frac{2}{\ln(1+\sqrt{2})} \simeq 2.269
$$
で与えられる温度 $T_{\text{C}}$ で相転移を示します.この温度 $T_\text{C}$ を臨界温度と言い,この付近で磁化は急激にゼロに近づき,比熱は発散します.
今回のシミュレーションでは,$L_x\times L_y$ 格子状2次元 Ising モデルのスピン1つ当たりのエネルギー,磁化,比熱の温度依存性をメトロポリスモンテカルロ法により再現し,相転移が起こっていることを確認します.
メトロポリスモンテカルロ法ミニマム
モンテカルロ法とは,乱数を用いた人工的なダイナミクスを導入することで物理系のシミュレーションを行う方法です.その中でも,系の分布の列を Markov 連鎖として生成する方法をメトロポリスモンテカルロ法と呼び,多粒子系の静的な性質を研究するために用いられます.
今回のシミュレーションでは,メトロポリスモンテカルロ法に従って,あるスピン配位 $C_k$ が与えられたときに,新たなスピン配位 $C_{k+1}$ を定めます.その概略は以下のようになります:
- スピン配位 $C_k$ に対し,無作為にスピンを選び,そのスピンを反転させた試行配位 $C_k'$ を作成する.
- 古いスピン配位と試行配位のエネルギー差 $\Delta E(C_k\to C_k')$ を計算する.
- エネルギーが増加する,即ち $\Delta E(C_k\to C_k')>0$ の場合,確率 $\exp[-\beta\Delta E(C_k\to C_k')]$ で $C_{k+1}=C_k'$ とし(試行配位の採択),確率 $1-\exp[-\beta\Delta E(C_k\to C_k')]$ で $C_{k+1}=C_k$ とする(試行配位の棄却).
- エネルギーが減少するなら,常に $C_{k+1}=C_k'$ とする.
この過程を繰り返すことで系のダイナミクスを再現し,系の平衡状態の性質を調べていきます.なお,メトロポリスモンテカルロ法を用いるためには,生成したい状態の集合が次の条件を満たしていなければなりません:
- 任意の状態が,他の任意の状態から高々有限回の過程の繰り返しによって到達できる.
- 周期性がない.
以上の条件を満たす Marcov 連鎖はエルゴード的であると言います.
シミュレーションの設定
今回は,以下の設定の下で Ising モデルのシミュレーションを行います:
- 格子のサイズは $50\times50$.
- $J=1,~h=0$.
- 格子の境界においては,周期的境界条件を課して計算を行う.
- メトロポリスモンテカルロ法の総ステップ数を $60000$,熱平衡に達するまでのステップ数を $10000$ とし,物理量は $10001$ ステップ目から $10$ ステップ間隔で値を記録し,平均をとる.
- 各種物理量を温度 $k_{\text{B}}T/J=0$ から $k_{\text{B}}T/J=5$ で計算.
コード
今回のシミュレーションのコードは以下のようになります.なお,このコードは文献2を参考に,一部変更を加えて作成しました.Julia1.8.2 を使用し,Jupyter Notebook 上で動作することを確認しています.
using Random
using Plots
using LaTeXStrings
# スピン配位の初期化
function spins_initialize(Lx, Ly, rng)
return rand(rng, [-1, 1], Lx, Ly)
end
# Siの計算
function Si_calculation(Ck, ix, iy, Lx, Ly)
jx = ix + 1
if jx > Lx
jx -= Lx
end
jy = iy
Si = Ck[jx, jy]
jx = ix - 1
if jx < 1
jx += Lx
end
jy = iy
Si += Ck[jx, jy]
jx = ix
jy = iy + 1
if jy > Ly
jy -= Ly
end
Si += Ck[jx, jy]
jx = ix
jy = iy - 1
if jy < 1
jy += Ly
end
Si += Ck[jx, jy]
return Si
end
# エネルギーの計算
function E_measure(Ck, J, h, Lx, Ly)
E = 0
for iy = 1:Ly
for ix = 1:Lx
Si = Si_calculation(Ck, ix, iy, Lx, Ly)
σi = Ck[ix, iy]
E += -(J/2)*σi*Si - h*σi
end
end
return E
end
# エネルギー差の計算
function ΔE_calculation(Ck, J, h, ix, iy, Lx, Ly)
Si = Si_calculation(Ck, ix, iy, Lx, Ly)
return 2J*Ck[ix, iy]*Si + 2h*Ck[ix, iy]
end
# メトロポリスモンテカルロ法によるスピンの更新
function spins_update(Ck, ix, iy, J, h, T, Lx, Ly, rng)
ΔE = ΔE_calculation(Ck, J, h, ix, iy, Lx, Ly)
σi = Ck[ix, iy]
σ_new = ifelse(rand(rng)≤exp(-ΔE/T), -σi, σi)
return σ_new
end
# メトロポリスモンテカルロ法の実行,各種物理量の計算
function Ising_Montecarlo(step_equilibration, step_MC, measure_interval, J, h, T, Lx, Ly)
rng = MersenneTwister(123) # 乱数の種
count_measure = 0 # 測定回数
E_mean = 0 # エネルギーの時間平均
E2_mean = 0 # エネルギーの2乗の時間平均
m_mean = 0 # 磁化の時間平均
absm_mean = 0 # 磁化の絶対値の時間平均
Ck = spins_initialize(Lx, Ly, rng)
for trial = 1:step_equilibration+step_MC
for ix = 1:Lx
for iy = 1:Ly
Ck[ix, iy] = spins_update(Ck, ix, iy, J, h, T, Lx, Ly, rng)
end
end
if trial > step_equilibration && trial % measure_interval == 0
count_measure += 1
E = E_measure(Ck, J, h, Lx, Ly) / (Lx*Ly)
E_mean += E
E2_mean += E^2
m = sum(Ck) / (Lx*Ly) # 磁化の計算
m_mean += m
absm_mean += abs(m)
end
end
E_mean /= count_measure
E2_mean /= count_measure
m_mean /= count_measure
absm_mean /= count_measure
C_mean = (E2_mean-E_mean^2) / T^2
return E_mean, m_mean, absm_mean, C_mean
end
# 上記の設定でシミュレーションを実行
function test()
step_equilibration = 10000 # 熱平衡に達するまでのステップ数
step_MC = 50000 # 時間平均計算に用いるステップ数
measure_interval = 10 # 数値の測定間隔
J = 1 # 交換相互作用定数
h = 0 # 外部磁場
Ts = range(0.01, 5, length=200) # 温度
Lx = 50 # 格子のサイズ
Ly = 50
E_T = [] # 各温度におけるエネルギー
m_T = [] # 各温度における磁化
absm_T = [] # 各温度における磁化の絶対値
C_T = [] # 各温度における比熱
# 各温度で各種物理量を計算,記録
for T in Ts
E_mean, m_mean, absm_mean, C_mean = Ising_Montecarlo(step_equilibration, step_MC, measure_interval, J, h, T, Lx, Ly)
push!(E_T, E_mean)
push!(m_T, m_mean)
push!(absm_T, absm_mean)
push!(C_T, C_mean)
end
# グラフ描画
plot(Ts, E_T, label="", xlabel=L"k_{\textrm{B}}T", ylabel="Energy", title="Temperature Dependence of Energy")
savefig("E_Tdep.png")
plot(Ts, m_T, label="", xlabel=L"k_{\textrm{B}}T", ylabel="Magnetization", title="Temperature Dependence of Magnetization")
savefig("m_Tdep.png")
plot(Ts, absm_T, label="", xlabel=L"k_{\textrm{B}}T", ylabel="Absolute Value of Magnetization", title="Temperature Dependence of Magnetization")
savefig("absm_Tdep.png")
plot(Ts, C_T, label="", xlabel=L"k_{\textrm{B}}T", ylabel="Specific Heat", title="Temperature Dependence of Specific Heat")
savefig("C_Tdep.png")
end
コードを読んでいただければわかると思いますが,文法がかなり Python に似ており,直感的に理解しやすいですよね.
結果
シミュレーションによって得られた結果を示します.
エネルギーの温度依存性
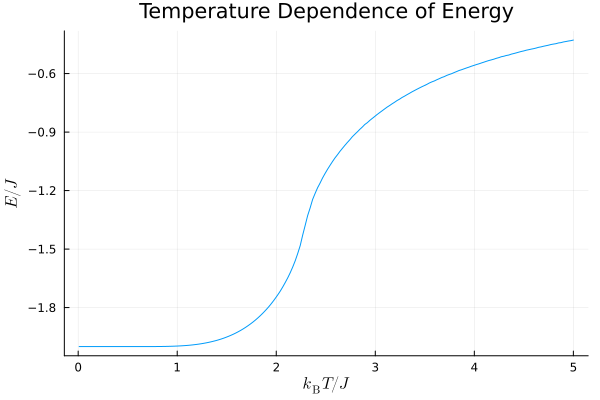
上図はエネルギーの温度依存性を示したグラフです.高温になるにつれて隣同士のスピンが反対向きになり,エネルギーが大きくなっていく様子がみられます.
磁化の温度依存性
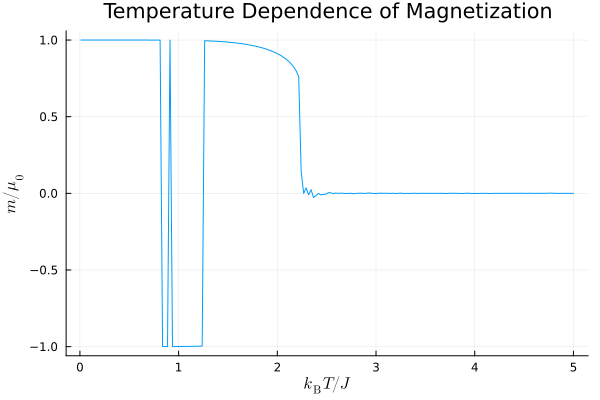
磁化の温度依存性は上図のようになります.低温側ではスピンが揃っているために磁化の絶対値は $\mu_0$ または $-\mu_0$ となっています.今回は外部磁場をゼロとしているために,スピンの揃う向きが「上向き」でも「下向き」でもエネルギーの値は変わりません.そのため,初期配位によってはどちらの向きにも揃い得ます.
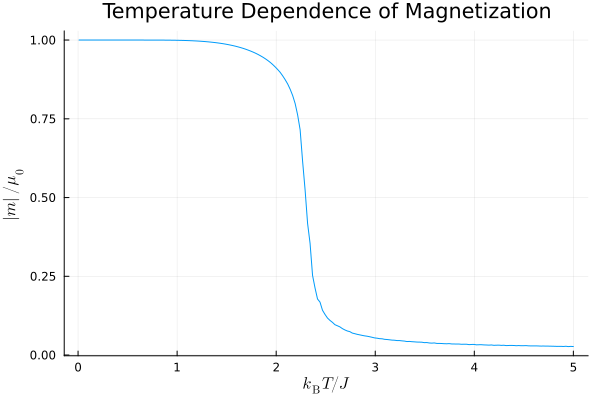
磁化の絶対値の温度依存性を示したこちらの図の方が分かりやすいですね.臨界温度付近で磁化が急激にゼロに近づいていく様子が見て取れます.
比熱の温度依存性
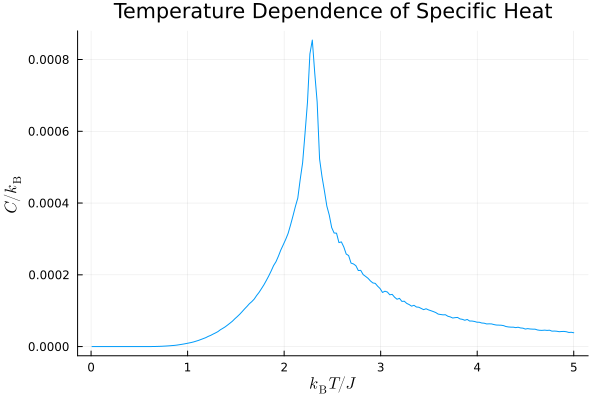
比熱の温度依存性は上図のグラフの通りです.臨界温度付近で値が急激に増加していますね.相転移の兆候が現れていると言って良さそうです.
まとめ
いかがだったでしょうか.Julia という言語を紹介しようと思い書き始めたものの,どうせならちょっと背伸びした題材にしようとした結果,当初の目的からは少しズレた中途半端な記事になってしまいました.
余談ながら,Julia のアドベントカレンダーも存在するようなのでこちらで紹介しておきます.
皆さんも Julia と共に良きシミュレーションライフを!
ありがとうございました.
参考文献
Julia については文献1, 2, 3を,Ising モデルについては文献4, 5, 6を,メトロポリスモンテカルロ法については文献7を参考にしました.
- Julia 1.8 Documentation https://docs.julialang.org/en/v1/
- Bogumił Kamiński, Przemysław Szufe(2019)「Julia プログラミングクックブック」オーライリー・ジャパン
- 永井佑紀(2022)「1週間で学べる! Julia 数値計算プログラミング」講談社
- 田崎晴明(2008)「統計力学1」(新物理学シリーズ37)培風館
- 田崎晴明(2008)「統計力学2」(新物理学シリーズ38)培風館
- 藤田重次(1990)「量子統計物理学」裳華房
- Jos. M. Thijssen(2003)「計算物理学」シュプリンガー・フェアラーク東京
特に,文献2は物理系の学生・研究者が Julia に入門する際にうってつけの1冊です.この記事で Julia に興味を持ってくださった方,ぜひ読んでみてください.