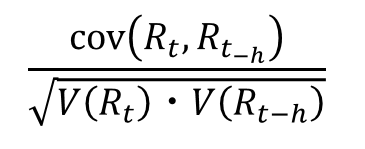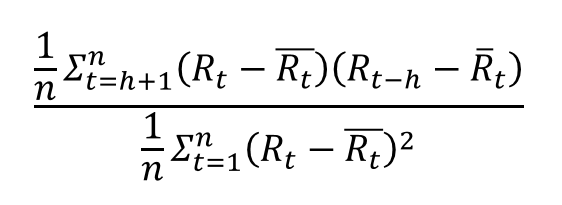導入
時間の経過に伴って変化するデータを示す、時系列データについての記事です。
時系列データは、自然科学、社会科学、経済学、金融、医療、エンジニアリングなど、多くの分野で扱われています。
今回はそんな時系列データを分析する際に重要なキーワードについての説明をします。
この記事では現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~ :横内 大介, 青木 義充 著(2014)のデータを使い、下記キーワードについてRで実行したあとに用語の説明をしていきます。
・自己相関係数
・ラグ
・偏自己相関係数
・推移率
・コレログラム
Rで実行
コードが非常に簡単なので先に紹介します。
使うデータはベクトル型の100日の収益データです。
str(X.return)
num [1:100] -3.85 4.64 2.25 1.53 5.15 ...
# 自己相関係数
# ラグ0から20までの自己相関係数を求める
acf(X.return,plot=F)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1.000 0.631 0.517 0.450 0.324 0.295 0.286 0.156 0.059 0.103 0.134 0.074 0.116 0.052 -0.087 0.020 -0.032
17 18 19 20
-0.014 0.027 -0.005 -0.020
自己相関係数はデフォルトに入っていいるacf関数にデータをいれてplot=Fにするだけです。
plot = T にすればコレログラムが書けます。
# 自己相関係数のコレログラムを描く
acf(X.return,plot=T)
type="p"を追記すれば偏自己相関係数の算出とプロットができます。
#type="p"で偏自己相関係数を求める
acf(X.return,plot=F,type="p")
Partial autocorrelations of series ‘X.return’, by lag
1 2 3 4 5 6 7 8
0.631 0.197 0.110 -0.063 0.061 0.079 -0.145 -0.129
9 10 11 12 13 14 15 16
0.134 0.148 -0.103 0.038 -0.045 -0.199 0.142 -0.078
17 18 19 20
0.106 0.047 -0.035 0.009
# 偏自己相関係数のコレログラムを描く
acf(X.return,plot=,type="p")
用語解説
自己相関係数
相関係数は2つの異なる変数xとyについての相関を見ていますが、
自己相関係数は現在の自分と過去の自分でどれだけ相関があるかという係数です。
ex.今日の株価は昨日の株価に影響している
式は次の通りです。
分子に共分散、分母は現在の分散と過去の分散の平方根です。
相関係数の式と似ていますね。
詳しく書くとこうです。
__n__は__データ数__を
__t__は__時点__を
__h__は__ラグ__を表します
ラグ
ラグとはずらず時点の度合いです
今日と昨日の相関を見るなら1日ずれているのでラグは1
今月と先々月の相関を見るならラグは2
といった具合です。
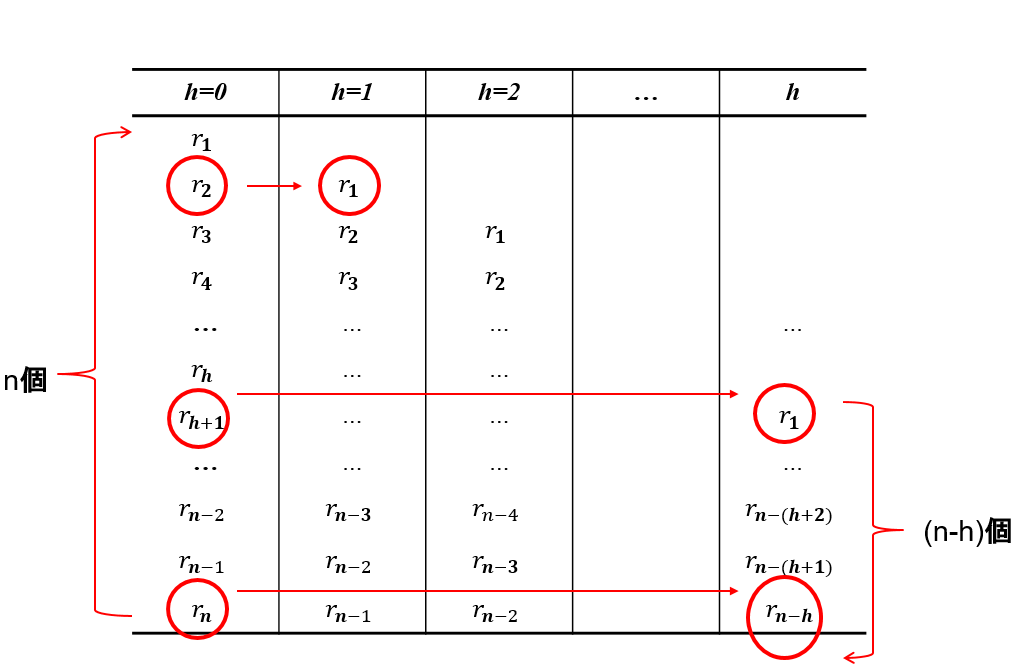
右にいくにつれてラグを1ずつズラしていく図を作りました。
rは各時点でのデータです。
ラグ1のときはr2に対応するのはr1
ラグhのときはr(h+1)に対応するのはr1
同じくラグhのときにrnに対応するのはr(n-h)
ラグhとの相関を見るときにはデータがn-h個しかないことがわかると思います。
このため自己相関係数の式に現れる過去に関する項はn-h個の和しかとれないため、h+1からnまでの和となっています。
コレログラム
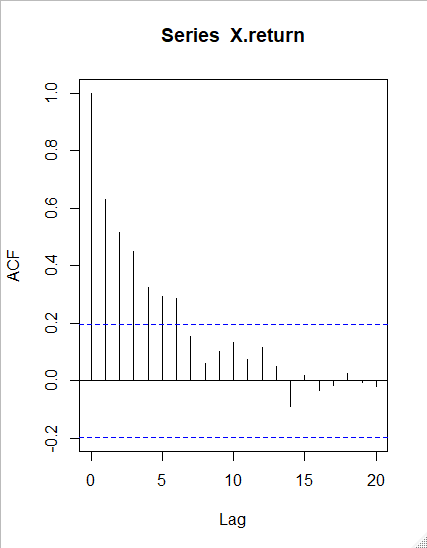
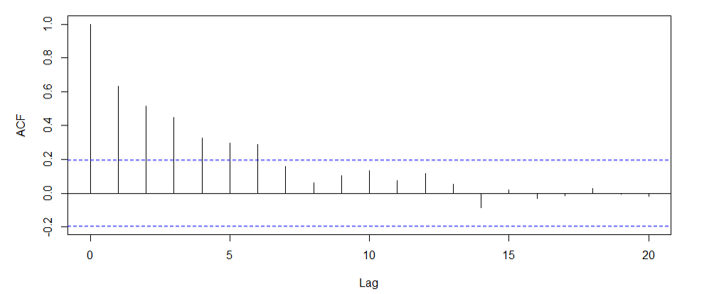
コレログラムとはそれぞれのラグについての自己相関係数を表した図です。
日ごとのある株の収益率データを使って見ていきましょう。
ラグ0は現在の自分と現在の自分の相関を表しているので当然1.0です。
右にいくほど下がっている、つまり過去にいくほど現在との相関が弱くなっていることがわかります。
ちなみに点線部は帰無仮説「自己相関係数が0である」の95%信頼区間です。
つまりこの点線の中におさまっていれば自己相関を持たない、つまり現在の自分と過去の自分は関係ないということです。
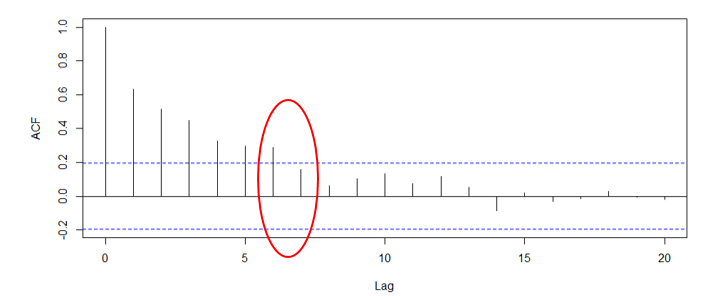
ラグ6に注目しましょう。
このコレログラムを素直に受け取れば現在と6日前までは自己相関があるということです。
この解釈が正しいかどうかは推移律という概念を使って考えましょう。
推移律
推移律とはaの値にはbの値を通じたcの値が関係するということです。
例えば、日ごとの収益率データに置き換えて考えてみましょう。
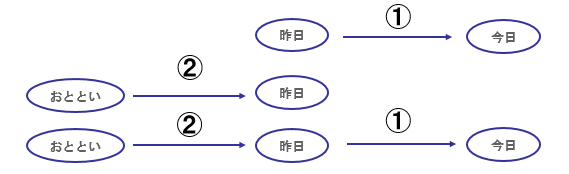
ex.「おととい」と「今日」の関係を見たいとき
① 今日の値には昨日の値が関係する
② 昨日の値にはおとといの値が関係する
① + ② = 今日の値には、昨日の値を通じたおとといの値が関係する
つまり現在と6日前の自己相関はラグ1からラグ5の影響、言い換えると1~5日前の影響があり、純粋に現在と6日前の相関関係を表していません。
純粋に今の値と過去の相関を見たいときに使うのが偏自己相関係数です。
偏自己相関係数
上で説明した通り推移律を考慮した自己相関係数です
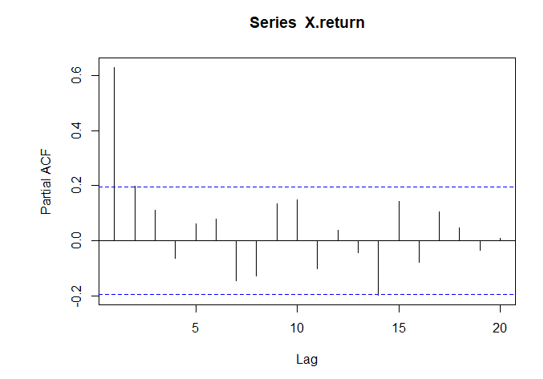
図で見てみましょう。
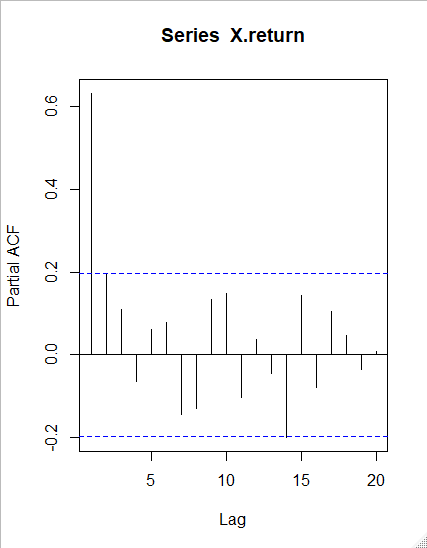
偏自己相関係数は自己相関と違い横軸がラグ1から始まり、縦軸の最大値も1ではありません。
見てわかる通りせいぜい自己相関があるのはラグ2までですね。
この図から現在の値と6日前の値は純粋には無関係であるということがわかります。
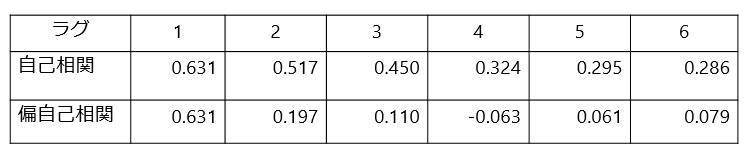
表の右下、ラグ6の偏自己相関係数は0.079と小さい値をとっていますね。
ラグ1に関してはどちらも同じ値0.631をとっていますね。
しかし厳密にはラグ1の自己相関係数 > ラグ1の偏自己相関係数だと考えています。
(※ あくまで私の個人的な見解であり、数学的な裏付けは一切できていません)
これには推移律と微分のような考えを組み合わせるとわかりやすいと思います。
今回はラグ1であれば今日と昨日という解釈でしたが、現在と24時間前という考えもできると思います。
現在と24時間前の自己相関は1時間前、2時間前...23時間前を通じていますね。
これを分単位、秒単位で推移律を考えるとラグが1でも自己相関係数より偏自己相関係数のほうが小さくなると考えました。
以上です、最後まで読んでいただきありがとうございました!
参考文献
現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~ :横内 大介, 青木 義充 著(2014)
一橋大学の横内先生と株式会社QUICKという金融情報サービス会社の青木さんの本です。
私みたいな時系列データ初学者にとって最適な入口となってくれた本です。
時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装:馬場真哉 著(2018)
経済・ファイナンスデータの計量時系列分析:沖本竜義 著(2010)