数学的な公式
組み合わせ計算は、数学的には以下の式で表現できます。
nCr=\frac{n!}{r!{(n-r)!}}
プログラムにおける問題
プログラミングにおいては数学の公式通りに計算して、組み合わせを求められるケースは少ないです。
理由は分子の階乗計算で、オーバーフローしてしまうからです。
n! = n\times(n-1)\times(n-2)\cdots2\times1
例えばn=13とするだけでint型の最大値を上回りオーバーフローします。
n=22とすると、long型でもオーバーフローします。
従って、公式通り計算することはできません。
そこでオーバーフローしにくい計算方法で実装することになります。
本稿では、パスカルの三角形を利用した計算方法を説明します。
パスカルの三角形を利用した計算
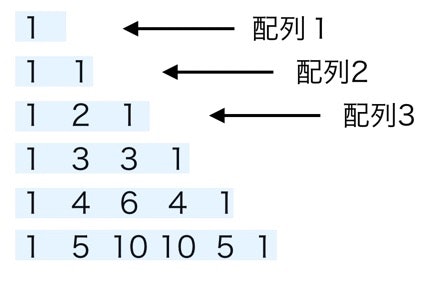
パスカルの三角形は以下の図の通りです。[1]
上段から順に、横並びの2数の和を1段下に記述していくことで作成できます。
組み合わせ計算の結果に対応することが知られていますので、これを利用します。
プログラムでは、事前にパスカルの三角形を2次元配列などに作成しておき、必要に応じて利用します。
パスカルの三角形を作成する際の計算は足し算のみで、階乗の計算がないため、公式よりもオーバーフローしにくくできます。
実装例
パスカルの三角形を二次元配列で作りきるところまで実装します。
1段目を1つの配列、2段目をまた別の配列といったようにして、1段を1配列で書きます。
上段から順番に埋めていきます。
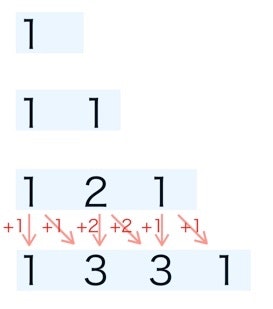
以下の図のように、上段の要素を、下段の真下と、1つ右に加えることでパスカルの三角形になります。
その他の条件
・計算量:nCrにおいて、n=2000くらいまで計算したいとします。
・オーバーフロー対策:組み合わせを考える問題では、計算過程だけでなく答そのものがオーバーフローするほど大きいことも珍しくないので、以下のように答えさせられます。
答えを計算し、 1000000007で割った余りを答えてください。
ここでは、このようなオーバーフロー対策の指定がある前提で実装します(つまり、1000000007の法の下で正しい実装)。
オーバーフロー対策の指定がない場合は、コメントで"オーバーフロー対策"と記した行を削除してください。
// 配列の準備
int c[][] = new int [2005][2005];//n=2000段作りきれるように、少し余裕を持って作成します。
//パスカルの三角形作成
int mod = 1000000007;// オーバーフロー対策:問題で指定されます。
c[0][0]=1;// 初期値として、最上部の1を与えます。
for(int i=0;i<2003;i++) {//2000段作りきるようにループを回します。細かい事を考えないで済むように少し余裕を持たせて回しています。
for(int j=0;j<2003;j++) {
long tmp = c[i][j]%mod;// オーバーフロー対策
c[i+1][j]+=tmp;
c[i+1][j+1]+=tmp;
}
}
完成です。
例えば、5C2を求めたい時には、c[5][2]で取得できます。
例題
ABC132 D問題 Blue and Red Balls
https://atcoder.jp/contests/abc132/tasks/abc132_d