Outline
- ベイズ推論における逆温度パラメータ
- 粒子フィルタ
- SMC Sampler
Intro
この記事では、ベイズ推定用ライブラリPyMCにあるMCMC実装の一種、sample_smcについて扱います。
MCMCによるベイズ推論は、多峰な事後分布形状に弱いという弱点があります。
単純な例として、やや離れた正規分布×2からMCMCでサンプリングしてみましょう。下図は、MCMCのデファクトスタンダードであるNUTS (No U-Turn Sampler) による結果です。
- 図:混合正規分布状の事後分布(緑)からNUTSで得たサンプリング結果(赤)
左側の正規分布から移動できず、右側の正規分布からはサンプリングできていないことがわかります。これは、2つのmode(事後確率の高い領域)の間に谷があり、MCMCサンプラーがこの谷を乗り越えられないことに起因します。
この問題に対処する代表的な方法として、レプリカ交換法があります。
しかしレプリカ交換法を使おうとすると、実用上の困難がいくつかあります。
- パラメータ(後述する逆温度の配置間隔)が難しい。
- 逆温度の配置間隔が開き過ぎていると失敗しやすい。配置感覚の経験則が知られているが、実際にはうまく行かないことが多い。
- 主要ライブラリには実装がない、もしくは古かったり不便なものしかない。
本記事では、レプリカ交換を代替し得る手法として、粒子フィルタ(パーティクルフィルタ)を応用した手法について説明します。
この手法の名前は分野によって微妙に異なるようですが、ここではPyMCに実装されているsample_smcに注目し、名前もこれに倣ってSMC Samplerと呼ぶことにします。
なお、本記事ではPyMC v5.0.2の実装を参照しています。今後バージョンの変化によって、記載内容が古くなることがあり得ます。
1. ベイズ推論における逆温度パラメータ
まず、SMCなどのMCMC手法で用いられる、ベイズ推論の「逆温度」を導入します。
1.1. 逆温度の導入
初めに、通常のベイズ推論をおさらいしておきます。
データ $X^{(n)}=\lbrace x_n \rbrace_{n=1}^N$ にモデル $p(x|\theta)$ を仮定し、そのパラメータ $\theta$ に事前分布 $p(\theta)$ を仮定したとき、パラメータ $\theta$ の事後分布は
p(\theta | X^{(n)}) := \frac{p(\theta) \prod_{n=1}^N p(x_n|\theta)}{Z_n(X^{(n)})}
となります。右辺分母の$Z_n(X^{(n)})$は、確率の総和が1になるようにする正規化定数です。
ここで事後分布をより一般に拡張し、逆温度$\beta$の事後分布
p_{\beta}(\theta | X^{(n)}) := \frac{p(\theta) \prod_{n=1}^N p(x_n|\theta)^{\beta}}{Z_n(X^{(n)}, \beta)}
を導入します。通常の事後分布との違いは、尤度が$\beta$乗されているという1点だけです。分母は同じく正規化定数ですが、$\beta$によって分子が変わるため分母も変わっています。
直感的には、逆温度$\beta$は尤度と事前分布のバランスを制御するパラメータと言えます。
事後確率最大化法(MAP推定)を行う場合、事前分布は正則化に相当しますから、逆温度は正則化の強さを制御するパラメータとみなすことができます。
この解釈については、カイヤンさんのブログ記事で詳しく紹介されていますので、ピンと来ない場合はこちらを参照してください。
1.2. 逆温度によるMCMCの改善
1.2.1. 事後分布形状への影響
事前分布が一様、あるいは極めて弱い弱情報事前分布であった場合を考えてみます。
その場合、事前分布による正則化の効果は殆どあるいは全くありませんから、逆温度$\beta$は尤度(そして事後分布)の形状を直接的に変動させるパラメータと見做せることになります。
βを1から小さくしていく場合を考えます。
$0<\beta<1$ の範囲で $\beta$ を小さくしていけば、尤度は平坦になっていきます。事前分布がほぼ平坦であれば、事後分布も平坦になります。
この性質を利用して、MCMCを改善することができます。
Introで述べた通り、MCMCは多峰分布からのサンプリングを苦手としています。そこで逆温度を$0<\beta<1$ に設定し、事後分布を平坦にすれば、この問題はある程度緩和できます。極論$\beta=0$ としてしまえば、尤度は完全に事前分布となり、サンプリングも容易になります。
ふつう事後分布の多峰性は尤度の複雑さに因るので、小さい逆温度は(多峰性など)事後分布の幾何的問題を緩和すると言えます。
ただし最終的に求めたいのは $\beta=1$ での事後分布ですから、逆温度を小さくするだけでは不足です。逆温度をMCMCと並行して変更したり、複数の逆温度設定でMCMCを並行させたりといった操作が必要になります。こうした逆温度の操作によって、多峰分布による問題を解決する方法が複数存在しています。
1.2.2. MCMCへの応用
単純な方法としては、 $\beta=0$ でのサンプリングから初めて、徐々に $\beta \to 1$ と大きくしていく方法が考えられます。
いわゆるバーンイン(初期値付近から抜け出すまで、初期のサンプリング結果を捨てる期間)において $\beta$ を動かし、その後は $\beta=1$ に固定すれば、本来の事後分布からサンプリングできます。バーンイン期間で $0<\beta<1$ とすることで、初期値付近のmodeから脱出する効果が期待できます。
これは最適化における焼きなましと同じ考え方です。
この方法は、初期値付近の比較的小さなmodeを脱出する程度であれば、十分に機能することがほとんどです。ただしIntroに示したような多峰事後分布では、両方のmodeからサンプリングすることはできません。
これは逆温度を単調増加させるため、一度 $\beta=1$ としてしまえば、あとは通常のMCMCと変わらないことによります。したがって、バーンイン以降のサンプリングでは、多峰性に対処することは望めません。
また別の広く知られた方法として、レプリカ交換法もあります。
これは異なる逆温度のMCMCサンプラーを並列に実行し、温度が隣接するサンプラー間で定期的に値を交換するものです。
この交換により、大きく遷移できる高温(逆温度の小さい)側の探索結果が、低温(逆温度の大きい)側に伝播される仕組みです。
ただしレプリカ交換法は、交換の存在ゆえに並列化が難しくなる、逆温度の配置が離れすぎると交換がなされない、といった問題があります。
(逆温度配置については理論値があるものの、経験上あまりうまく動作しません。)
別の方法を考える前に、寄り道して時系列モデルにおけるベイズ推定について説明します。
2. 粒子フィルタ
Sequential Monte Carlo(以下SMC)は、時系列モデルとくに非線形・非正規な状態空間モデルの学習のために考案された、MCMCの一種です。粒子フィルタ(パーティクルフィルタ)とも呼ばれます。
本記事では、後述のSMC Samplerとの混同を防ぐため「粒子フィルタ」とだけ呼ぶことにします。
粒子フィルタの詳細は、下記の書籍を参照してください。本章は概要のみを記載します。
また、状態空間モデルや粒子フィルタについて既知の場合は読み飛ばしてください。
2.1. 状態空間モデルの推定
時系列データ $\lbrace y_t\rbrace_{t=1}^T$ があり、状態空間モデル
\begin{align}
&y_0 \ \ \ \quad y_1 &y_T\\
&↑ \qquad ↑ &↑ \\
&x_0 \rightarrow x_1 \to \ ... \ \to &x_T
\end{align}
に従っているとします。これは
- 観測できない内部状態 $x_t$ が何らかのモデル(内部状態モデル)に従って $x_{t+1}$ に遷移し
- そこに観測ノイズが乗った $y_t$が観測される
とするモデルです。
内部状態モデルは、ランダム性を表すノイズ項$ v_t$と、決定論的な遷移関数$f$を用いて
$$x_{t+1} = f(x_t, v_t)$$
と表現することが一般的です。
これに観測ノイズ$\epsilon_t$が加わって、観測値
$$y_t = x_t + \epsilon_t$$
となります。
状態空間モデルを用いた時系列解析では、直接観測できない内部状態 $\lbrace x_t\rbrace_t^T$ を推定する・未来の$\lbrace x_t \rbrace_{t>T}, \lbrace y_t\rbrace_{t>T}$を予測することを考えます。
状態空間モデルが線形正規であれば、推定・予測はカルマンフィルタで実行できます。カルマンフィルタは非線形な場合にも拡張でき、拡張カルマンフィルタ(EKF)・無香カルマンフィルタ(UKF)などのアルゴリズムが存在します。しかし非線形性が強い場合などには適応しきれないため、モンテカルロ近似を用いた粒子フィルタを用います。
2.2. 粒子フィルタ
粒子フィルタ(パーティクルフィルタ)は、観測 $\lbrace y_t\rbrace_{t=1}^T$ から内部状態の分布 $p(x_t | \lbrace y_t \rbrace_{t=1}^T)$を推定するアルゴリズムです。
本節では、そのアルゴリズムの概要を示します。
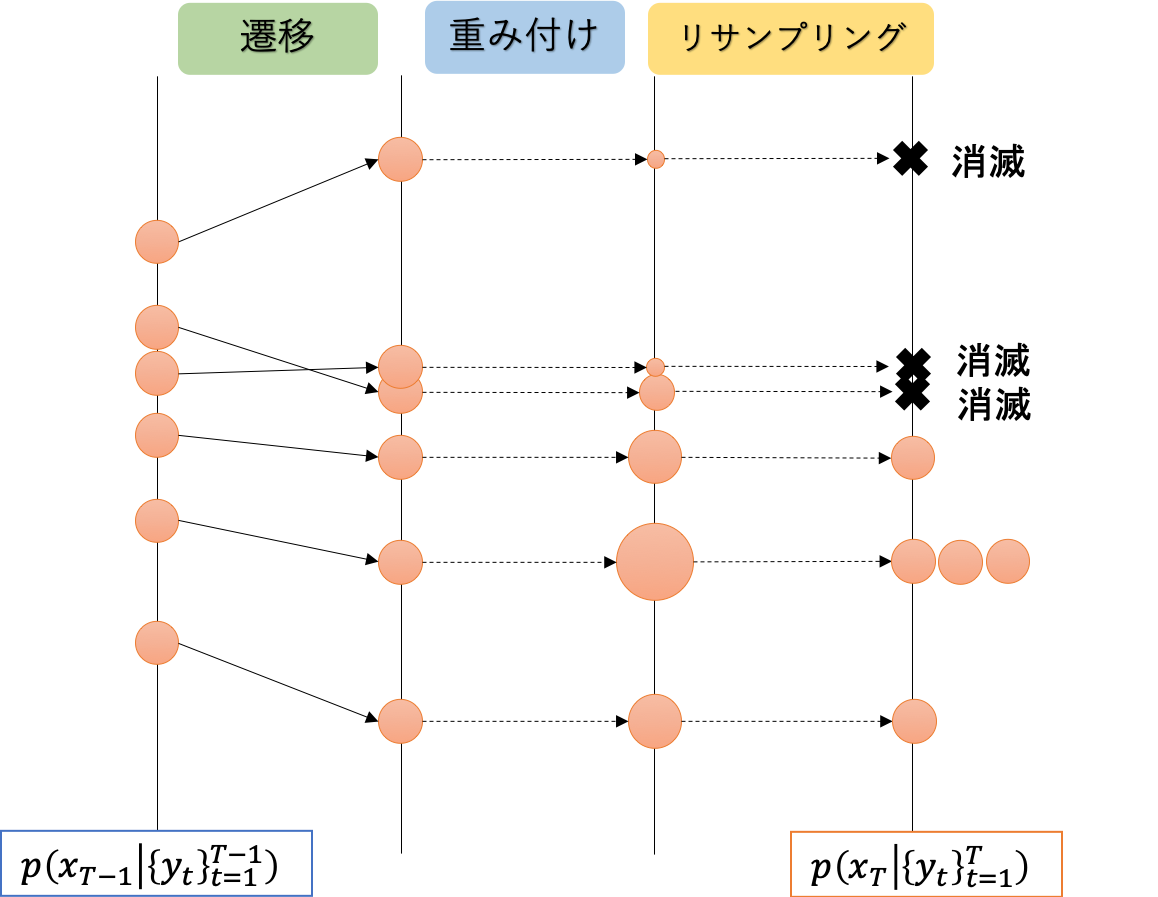
- 時刻 $t-1$における事後分布 $p(x_{T-1} | \lbrace y_t\rbrace_{t=1}^{T-1})$ をモンテカルロ近似したサンプル
$$x_{T-1}^{(i)} \sim p(x_{T-1} | \lbrace y_t\rbrace_{t=1}^{T-1})$$
がある。 - $\lbrace x_{T-1}^{(i)} \rbrace$を状態区間モデル(の内部状態モデル)に従って遷移させ、新しいサンプルを生成する。
内部状態モデルのノイズ$v_{T-1}$は乱数で生成する。
$$x_T^{(i)} = f(x_{T-1}^{(i)}, v_{T-1}^{(i)})$$ - 時刻Tでの観測値 $y_T$を取得し、その尤度 $p(y_T | x_T^{(i)})$から、サンプル $x_T^{(i)}$の重み $w_T^{(i)}$を計算する。
$$w_T^{(i)} := \frac{p(y_T | x_T^{(i)})}{\sum_i{p(y_T | x_T^{(i)})}}$$ - 各サンプルを重みに従って再サンプリングする。
すなわち、確率 $\frac{w_T^{(i)}}{\sum_i{w_T^{(i)}}}$で $x_T^{(i)}$をサンプリングし、所定回数くり返した結果を$p(x_T | \lbrace y_t\rbrace_{t=1}^T)$のモンテカルロ近似とする。 - $T-1 \leftarrow T$として、2.に戻る。
まとめると
- (1.では)時刻$1\sim T-1$までの観測値から求めた時刻$T-1$での内部状態の事後分布があり
- (2.で)時刻$T$の内部状態$x_T$の予測サンプルを生成し
- (3.と4.で)時刻$T$の観測$y_T$を取得したのち、予測分布を修正する
という手順を踏んでいます。
このアルゴリズムはベイズ推論を逐次的に実行しているのですが、その妥当性は次節で追っていきます。
2.3. ベイズ推論としての解釈
本節では、上に記した粒子フィルタのアルゴリズムが、内部状態の分布 $p(x_t | \lbrace y_t\rbrace_{t=1}^T)$のベイズ推定になっていることを確認します。
モンテカルロ近似を行うには、
- 対象空間上を満遍なくサンプリングし
- 各サンプルが所望の分布に従っていなければならない。
ここでは事後分布 $p(x_T | \lbrace Y_t \rbrace_{t=1}^T)$ をサンプリングしたいので、サンプル $x_T^{(i)}$を得る確率は
$$p(x_T = x_T^{(i)}| \lbrace Y_t\rbrace_{t=1}^T)$$
でなければなりません。
これは事後分布の下で$x_T=x_T^{(i)}$となる確率です。
通常のベイズ推定であれば、MCMCによって上記の条件1, 2を満たすサンプルを直接ターゲット分布から取得できます。
しかし粒子フィルタでは2.が満たされていません。
(1.は初期状態$x_0$でサンプルを満遍なく配置し、それを遷移させることで満たしている。はず。)
そこで各サンプルの事後確率 $p(x_T = x_T^{(i)}| \lbrace Y_t \rbrace_{t=1}^T)$を求めて、確率の調整を行います。
2.3.1. 事後確率の計算
上に見た通り、サンプル $x_T^{(i)}$を得る確率は、事後分布上で$x_T=x_T^{(i)}$となる確率、としなければなりません。
この確率を計算してみると、
\begin{align}
& p(x_T = x_T^{(i)}| \{Y_t\}_{t=1}^T) \\
&= \frac{p(y_T, x_T^{(i)}|\{Y_t\}_{t=1}^{T-1})}{ p(y_T|\{Y_t\}_{t=1}^{T-1})} \\
&= \frac{p(y_T | x_T^{(i)}) p(x_T^{(i)}|\{Y_t\}_{t=1}^{T-1})}{\sum_i{p(y_T | x_T^{(i)}) p(x_T^{(i)}|\{Y_t\}_{t=1}^{T-1})} } .
\end{align}
ここで、$p(x_T^{(i)}|{Y_t}_{t=1}^{T-1})$は実際に各サンプルが得られる確率です。これはiによらず$1/N$となります。
実際、前時刻での事後分布から得たサンプル
$$x_{T-1}^{(i)} \sim p(x_{T-1} | \lbrace y_t \rbrace_{t=1}^{T-1})$$
を次時刻に遷移させたのが $x_T^{(i)}$なので、事後分布をモンテカルロ近似していることから
\begin{align}
p(x_T^{(i)}|\{Y_t\}_{t=1}^{T-1}) &= p(x_{T-1}^{(i)}|\{Y_t\}_{t=1}^{T-1}) \\
& \approx \frac{1}{N} \sum_{n=1}^N{\delta (x_{T-1}^{(i)} - x_{T-1}^{(n)})} \\
& = \frac{1}{N}
\end{align}
となります($\delta$はデルタ関数です)。
したがって、
\begin{align}
& p(x_T = x_T^{(i)}| \{Y_t\}_{t=1}^T) \\
&= \frac{p(y_T | x_T^{(i)}) /N}{\sum_i{p(y_T | x_T^{(i)}) /N} } \\
&= \frac{p(y_T | x_T^{(i)})}{\sum_i{p(y_T | x_T^{(i)})}}
\end{align}
これは粒子フィルタで用いた、各サンプルの重み $w_T^{(i)}$そのものです。すなわち、
$$w_T^{(i)} = p(x_T = x_T^{(i)}| {Y_t}_{t=1}^T) .$$
この重み $w_T^{(i)}$と、サンプル $x_T^{(i)}$を得る確率を一致させれば良い、ということが分かりました。
2.3.2. 再サンプリングによる確率の調整
続いて、この重みによる確率の調整を行います。
これは単純に、$\lbrace x_T^{(i)}\rbrace_{i=1}^N$から確率$w_T^{(i)}$で$x_T^{(i)}$を引く……という復元抽出をくり返すだけです。
この復元抽出をN回くり返せば、得られたサンプルは事後分布$p(x_T | \lbrace Y_t\rbrace_{t=1}^T)$に従っており、事後分布をモンテカルロ近似することができます。
この過程を再サンプリングと呼びます。
ここまでで重要なのは、粒子フィルタが既に多峰事後分布に対応しているということです。
$x_T$の事後分布を直接サンプリングすると多峰性に阻まれますが、サンプリング容易な時刻0の$x_0$から初めて、$x_0$の各サンプルを遷移させれば、多峰性にかかわらず$x_T$をサンプリングできます。
3. SMC Sampler
粒子フィルタを転用して通常のMCMCを行う手法として、PyMCに実装されているSMC samplerを説明します。
粒子フィルタを通常のMCMCに転用しようとする試みは他にもいくつか存在するようですが、細部を除いてほぼ同一のようです。
- likelihood temperingと呼ぶ向きもあり、化学分野で応用例がある。
- 参照を辿っていくとウプサラ大学の資料に行き着く。ここでも"likelihood tempering"と呼ばれている。
本記事では、PyMCのドキュメントにある元論文+PyMC実装sample_smc()に沿って説明します。
- 元論文:“Transitional Markov Chain Monte Carlo Method for Bayesian Model Updating, Model Class Selection, and Model Averaging”
pymc.smc.sample_smcの公式ドキュメント
3.1. SMC Samplerの概要
粒子フィルタが時刻ごとに変化する内部状態(とそこから得られた観測値)を扱っていたのに対して、SMC Samplerはモデルとデータは固定のまま、逆温度が遷移していく状況を考えます。
モデル$p(x|\theta)$と事前分布$p(\theta)$にデータセット$X^{(n)}$が与えられ、事後分布 $p(\theta | X^{(n)})$を求めたい場合、通常であればMCMCで事後分布に従うサンプルを取得します。
しかし事後分布 $p(\theta | X^{(n)})$に多峰性など幾何的な問題がある場合、NUTSのようなMCMCは機能せず、逆温度操作に頼ることになります。
§1と同様に、逆温度$\beta$での事後分布を $p_{\beta}(\theta | X^{(n)})$ と書くことにしましょう。
SMC Samplerでは逆温度を0→1へと段階的に遷移させ、粒子フィルタと同様にして $p_{\beta=0}(\theta | X^{(n)})$でのサンプルから $p_{\beta=1}(\theta | X^{(n)})$を生成します。
細部は後述するとして、アルゴリズムの概要を示します。
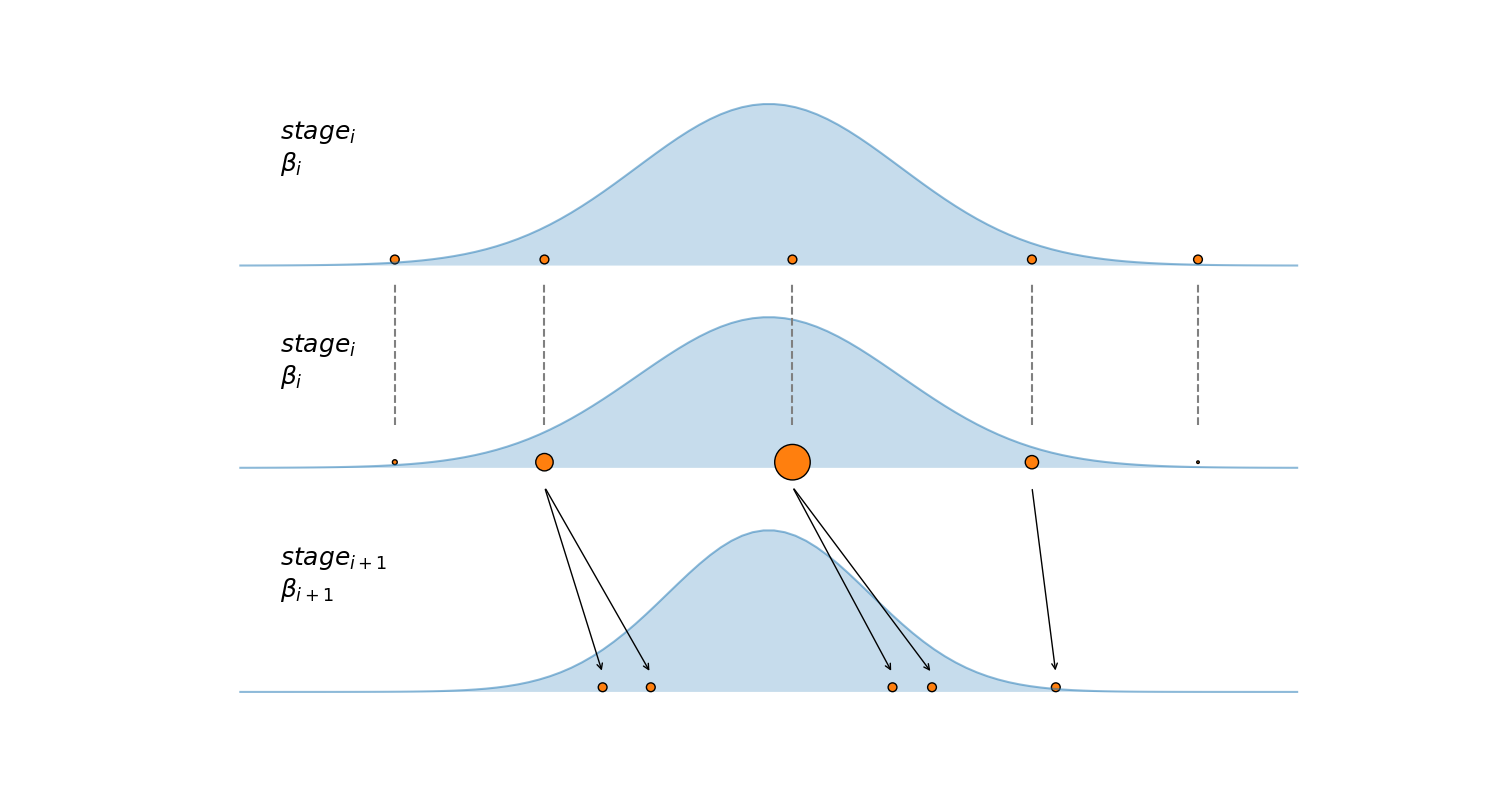
上図:PyMCの公式ドキュメントより引用
- 初期状態
- 逆温度の初期値を$\beta_0=0$とする。このとき$$p_{\beta=0}(\theta | X^{(n)}) = p(X^{(n)}|\theta)^0 p(\theta)=p(\theta) .$$
事後分布は事前分布と一致するので、事前分布 $p(\theta)$ からN個のサンプルを取得する。
取得したサンプルを $\lbrace \theta_0^{(i)} \rbrace_{i=1}^N$ とし、これを更新していく。
- 逆温度の初期値を$\beta_0=0$とする。このとき$$p_{\beta=0}(\theta | X^{(n)}) = p(X^{(n)}|\theta)^0 p(\theta)=p(\theta) .$$
- 現状のサンプル$\lbrace \theta_j^{(i)} \rbrace_{i=1}^N$の有効サンプルサイズ(ESS)を計算し、それを元に$\beta$の増加幅$\Delta_j$を決める。 $$\beta_{j+1} := \beta_j + \Delta_j.$$
- 増加した $\beta_{j+1}$ のもとで各サンプルの事後確率を計算し、再サンプリングの重み $\lbrace w_j^{(i)} \rbrace_{i=1}^N$ を計算する。
- 重み$\lbrace w_j^{(i)}\rbrace_{i=1}^N$を付けた再サンプリングを実行し、逆温度 $\beta_{j+1}$ でのサンプル $\lbrace \theta_{j+1}^{(i)}\rbrace_{i=1}^N$ を得る。
- 各サンプル$\theta_{j+1}^{(i)}$を始点としたMCMC(通常はMetropolis-Hastings)を行い、サンプルをカサ増しする。
- $\beta=1$に到達するまで1~4をくり返す。
いくつかの相違点はあるものの、大筋は粒子フィルタと同じ流れになっています。
主な相違点としては、
- 逆温度$\beta$の増加幅を決定する処理(→§3.2.1)
- 再サンプリングに用いる重みの計算方法(→§3.2.2)
- 各時刻(逆温度値)において、都度MCMCを実行してサンプルをカサ増しする処理(→§3.2.3)
といった点が挙げられます。これらについては、続く3.2節で説明します。
3.2. 詳細
3.2.1. 逆温度の配置設定
逆温度を用いたMCMC手法において、逆温度の配置はかなり重要な意味を持ちます。
- 類似手法のレプリカ交換法では、隣接レプリカ(MCMCサンプラー)間で逆温度の差が大きすぎると、「交換」が棄却されやすくなり、逆温度操作による恩恵(多峰性への対応など)が得られません。しかし配置を詰めすぎると、計算コストが増大します。
- SMC Samplerでも、遷移する逆温度の差が大きすぎると、再サンプリング時に多くのサンプルが消滅することになります。これは非効率なだけでなく、サンプルが広い領域をカバーできなくなるため、モンテカルロ近似の精度確保の上で致命的です。
- これは $p_{\beta_j}(\theta | X^{(n)})$と $p_{\beta_{j+1}}(\theta | X^{(n)})$の違いが大きくなると、前者から得たサンプルが後者に適合しなくなることによります。
- 逆温度の配置を詰めすぎると計算コストが増大するのも同様です。しかもここは並列化できないため、直接計算時間に影響します。
この問題に対して、SMC Samplerではサンプリング効率を確認しながら、逐次的に逆温度間隔を決めることができます。
元論文とPyMC実装で微妙な違いがあるようですが、ここではPyMC側に従います。
一般に、MCMCで得たサンプルは有効サンプルサイズ(ESS)によって評価されます。
粒子フィルタのESSは
ESS = \frac{1}{\sum_{i=1}^N{(w_j^{(i)}})^2}
と定義されます。
PyMCのSMC Samplerでは、このESSが大幅に低下しないように$\beta$の増分を決定します。
デフォルト設定では、ESSがサンプルサイズ×0.5を下回らない範囲で$\beta$を増やすようです。この倍率はMCMCカーネルの引数thresholdとして指定できます。
この処理は、各MCMCカーネルのupdate_beta_and_weights()関数で実装されています。リンク先のGitHubにコードがありますので参照してください。
3.2.2. 重みの導出
再サンプリング時の重みは、各時刻での事後確率として設定する必要がありました。
粒子フィルタでは各時刻における(各サンプルの)尤度に一致しましたが、SMC Samplerでは前時刻との尤度比となります。
\begin{align}
p_{\beta_{j+1}}(\theta_{j+1}^{(i)} | X^{(n)})
&= p(X^{(n)}|\theta_{j+1}^{(i)})^{\beta_{j+1}} p(\theta_{j+1}^{(i)}) / Z_n(X^{(n)}, \beta_{j+1}) \\
&= p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1}} p(\theta_{j}^{(i)}) / Z_n(X^{(n)}, \beta_{j+1}) \\
&= p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j} \frac{p(X^{(n)}|\theta_{j}^{(i)})^{\beta_j} p(\theta_{j}^{(i)})}{Z_n(X^{(n)}, \beta_{j+1})} \\
&= p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j} p_{\beta_j}(\theta_j^{(i)} | X^{(n)}) \frac{Z_n(X^{(n)}, \beta_j)}{Z_n(X^{(n)}, \beta_{j+1})} \\
&= p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j} \frac{1}{N} \frac{Z_n(X^{(n)}, \beta_j)}{Z_n(X^{(n)}, \beta_{j+1})} \\
&\propto p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j} .
\end{align}
§2.3.1と同様、$\lbrace \theta_{j}^{(i)}\rbrace$が事後分布をモンテカルロ近似していることを用いています。
また$Z_n(X^{(n)}, \beta)$は、§1にも登場した、事後分布の正規化定数です。
したがって、再サンプリングの重みは(正規化して)
$$w_j^{(i)} := \frac{p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j}}{\sum_{i=1}^N{p(X^{(n)}|\theta_{j}^{(i)})^{\beta_{j+1} - \beta_j}}}$$
となります。
3.2.3. 通常MCMCの実行
SMCでは時刻jが進むほど、再サンプリングによって独立なサンプルが減少し、モンテカルロ近似の精度が低下します。
これは尤度の大きいサンプルが複数個生成され、尤度の低いサンプルが消滅していくためです。
開始時点でN通りのサンプルを確保していても、再サンプリングによってj個のサンプル消滅すれば、N-j個のサンプルを使い回した結果を得ることになります。
Nがjより十分大きければ分布の要点を掴むことはできますが、モンテカルロ近似の精度を効率的に(Nをあまり増やさずに)確保することが理想です。
SMC Samplerでは、サンプルの「カサ増し」 のため $\beta_j \rightarrow \beta_{j+1}$の遷移と再サンプリングを終えた後に、通常のMCMCを行います。
これによって、$\theta_{j+1}^{(i)}$の周辺をサンプリングすることができ、サンプルの多様性を回復できます。
再サンプリングでは、尤度の高い領域において同じサンプルが複数個されてしまいますが、これをバラつかせて有効活用することにもつながります。
PyMC実装では、再サンプリング後の$\theta_{j+1}^{(i)}$を始点として、Metropolis-Hastings法による行っています。
遷移核(提案分布)は正規分布としますが、その平均分散の設定は元論文とPyMCで微妙に異なるようです。
PyMCでは、提案分布の平均は遷移後の各サンプル$\theta_{j+1}^{(i)}$で固定です。
また分散は、サンプルの分散($\approx$事後分布の分散)を計算しているようです。
これは、MCMCを行う前から事後分布の概観が(サンプルとして)得られているため、その形状にあった提案分布を作ってしまえば、棄却が少なく効率的になる、という理由と考えられます。
この提案分布の調整は、各MCMCカーネルのtune()関数で実行されています。
得られた遷移核にしたがって、Metropolis-Hastings法によるサンプリングが実行されます。
このサンプリングの停止基準は、サンプルの自己相関によって定められています。
- 「サンプル間の自己相関の変動が閾値以上となる組み合わせが9割以上」となる間は継続、そうでなければ自己相関が下がらなくなったとして停止、のようです。
サンプリングに関する処理は、各MCMCカーネルのmutate()関数に記述されています。気になる場合はコードを確認してみてください。
まとめ
PyMCに実装されているSMC Samplerについて、アルゴリズムを概観しました。
- 粒子フィルタによる逐次的に変化する分布からのサンプリングと、レプリカ交換法のような逆温度操作による多峰分布への対応を併せることで、事後分布形状への対応を可能にしています。
- また粒子フィルタの持つ弱点であるサンプルの多様性減少という問題を、各時刻で別途MCMCを行うことで克服しています。
- このMCMCでは、既にある程度まで事後分布を近似したサンプルが得られているため、そのサンプルから効率的な提案分布を作ることができます。
- 逆温度操作を用いたMCMC手法の難点であった逆温度の配置間隔についても、粒子フィルタの有効サンプルサイズを用いて動的に決定することができます。
本記事ではアルゴリズムの概要説明に徹し、実例までは扱えませんでした。
続編……が書けるかどうかわかりませんが、あればそちらに持ち越したいと思います。
参考(になりそうな)文献
- 逆温度について
- 渡辺澄夫:『ベイズ統計の理論と方法』
- 『計算統計Ⅱ』
- 粒子フィルタについて
- 樋口知之:『予測にいかす統計モデリングの基本』
- 北川源四郎:『時系列解析入門』
- Sarkka:"Bayesian Filetering and Smoothing"
- SMC samplerについて