変分問題(概略)
通常の最適化問題は, ある目的関数が最小(もしくは最大)となるような変数の値を見つける問題ですが, 変数ではなく最適な関数を見つけるのが変分問題(Variational Problem)1, 2です。
目的関数は関数を引数とする関数$F$によって次の形で書かれるのが一般的です。
\displaystyle {\rm Minimize}\,\,\,\int_{a}^{b}F(x, u(x), u'(x))dx
上記の目的関数は汎関数(関数に対して一つの値を対応させるもの)と呼ばれます。
これに制約として端点条件などを加えて, 汎関数を最小にするような関数$u$を求めます。
変分問題の解法としてはオイラー・ラグランジュ(Euler-Lagrange)方程式を用いるのが一般的で, 最適関数$u$の必要条件として次の微分方程式を与えます。
\cfrac{\partial F}{\partial u} - \cfrac{d}{dx}\cfrac{\partial F}{\partial u'} = 0
導出方法などは割愛します。次を参照にしてください3, [4][寒野善博, 土屋隆, 最適化と変分法]。
以下では見やすくするために $\frac{\partial F}{\partial u}$ を $F_u$ と記載することにします。また$u(x)$を引数を省略して$u$と書くこともあります。
さて, 簡単な例で計算してみましょう。
計算例1(初期条件なし)
F(x, u(x)) = x^2u(x) + xu(x)^2\\
\displaystyle {\rm Minimize}\,\,\,\int_{a}^{b}F(x, u(x))dx
$F(x, u(x))$の形の場合は, オイラー・ラグランジュ方程式の第二項が0になるので実質, 関数$u$が満たすべきなのは
F_u = 0
という微分方程式になります。 $F_u$は関数$u$を変数とみなして$F$を微分したものになるため,
F_u = x^2 + 2xu
なので,
F_u = 0 \iff x^2 + 2xu = 0
より
u(x) = -\cfrac{x}{2}
が解として得られます。
計算例2(初期条件あり)
F(x, u(x)) = x^2u(x) + xu(x)^2\\
\displaystyle {\rm Minimize}\,\,\,\int_{a}^{b}F(x, u(x))\\
{\rm s.t.}\,\,\,\,\,\,\,\,u(a) = u_a
今度は計算例1に端点条件がついています。 計算例1と同様にオイラー・ラグランジュ方程式$F_u = 0$を解くと, $u(x) = -\frac{x}{2}$が出てきますね。ん? この時点で関数の形が一意に定まるので, 端点条件を満たせないではないか? と思われることでしょう。実はその通りで, $F(x, u)$の形のときは端点条件を満たすような連続関数$u$は一般には存在しません。
上記の問題の解は
u(x) = \begin{cases}
u_a & (x = a) \\
-\frac{1}{2} & (a < x \leq b)
\end{cases}
となります。
しかし, **「端点条件を満たす連続関数$u$が欲しい!」**という思いがあるときは, 何らかの工夫をしなければなりません。
そこで$\frac{d}{dx}F_{u'} = 0$とならないように新しい項を$F$に付け加えるのはどうでしょうか。
F(x, u) = x^2u + xu^2 \rightarrow F(x, u, u') = x^2u + xu^2 + xuu'
この場合のオイラー・ラグランジュ方程式を計算してみます。
F_u = x^2 + 2xu + xu'\\
F_{u'} = xu \rightarrow \frac{d}{dx}F_{u'} = u + xu'
これより
F_u - \frac{d}{dx}F_{u'} = 0 \iff x^2u + xu^2 + xu' - u - xu' = x^2u + xu^2 - u = 0
またもや, 微分方程式ではなく関数恒等式となり, 関数$u$が一意に定まってしまいました。
結局のところ
F = M(x, u) + N(x, u)u'
の形の関数はオイラー・ラグランジュ方程式が関数恒等式となります。
計算例3(初期条件あり)
F(x, u(x), u'(x)) = x^2u(x) + xu(x)^2 + \alpha u'(x)^2\\
\displaystyle {\rm Minimize}\,\,\,\int_{a}^{b}F(x, u(x), u'(x))\\
{\rm s.t.}\,\,\,\,\,\,\,\,u(a) = u_a
計算例2の関数に$\alpha u'(x)^2$を追加した問題です。$\alpha$はパラメータで, その絶対値が小さいほど元の問題(計算例2)に近づきます。
F_u = x^2 + 2xu\\
F_{u'} = 2\alpha u' \rightarrow \frac{d}{dx}F_{u'} = 2\alpha u''
これより, オイラー・ラグランジュ方程式を適用すると
F_u - \frac{d}{dx}F_{u'} = 0 \iff u'' = \cfrac{1}{2\alpha}(x^2 + 2xu) \cdots (i)
という微分方程式が得られます。
あとはこれを解けば終わりですが, 解析的に解くことが難しいときは数値的に解軌跡の近似を行います。
$(i)$は
u \leftarrow u, \,\,\,\,\, v \leftarrow u'
として
\begin{cases}
u' = v\\
v' = \cfrac{1}{2\alpha}(x^2 + 2xu)
\end{cases}
という連立1階微分方程式に変換できます。これに対して, 常微分方程式の数値解析手法を適用していきます。
import numpy as np
import matplotlib.pyplot as plt
def f(t, u):
alpha = 0.01 # パラメータ
return (t*t + 2*t*u) / (2*alpha)
a = 0 # 積分区間始点
b = 2 # 積分区間終点
N = 10000 # 区間区切り数
T, h = np.linspace(a, b, num=N, retstep=True) # [a, b]をN分割する, hは区切り幅
U = np.array([[0, 0] for _ in range(N)], dtype='float32') # U[:, 0] u, U[:, 1] v グラフ描写のために各点における関数uとvの値を保存
# 初期条件の設定
U[0, 0] = 5 # uの初期点での値
U[0, 1] = 0 # vの初期点での値
計算条件は積分区間$[0, 2]$として, 区切り数は$N=10,000$としました。
各手法の更新式6を実装すると次のようになります。
初期条件は$u(0) = 5, u'(0) = 0$としました。
# Euler method
for i, t in enumerate(T[1:], 1):
U[i] = U[i-1] + [h*U[i-1, 1], h*f(t-h, U[i-1, 0])]
# Heun method
for i, t in enumerate(T[:-1], 1):
U[i, :] = U[i-1, :] + h*np.array([U[i-1, 1], (f(t-h, U[i-1, 0]) + f(t, U[i-1, 0]+h*f(t-h, U[i-1, 0]))) / 2])
# Adams-Bashforth method
for i, t in enumerate(T[:-1], 1):
if i == 1:
U[i] = U[i-1] + h*(f(t-h, U[i-1, 0]) + f(t, U[i-1]+h*f(t-h, U[i-1, 0]))) / 2
else:
U[i] = U[i-1] + h*(3*f(t-h, U[i-1, 0]) - f(t-2*h, U[i-2, 0])) / 2
# Runge-Kutta method
for i, t in enumerate(T[:-1], 1):
k1 = f(t-h, U[i-1, 0])
k2 = f(t-h/2, U[i-1, 0]+h*k1/2)
k3 = f(t-h/2, U[i-1, 0]+h*k2/2)
k4 = f(t, U[i-1, 0]+h*k3)
U[i] = U[i-1, 0] + h*(k1 + k2 + k3 + k4) / 6
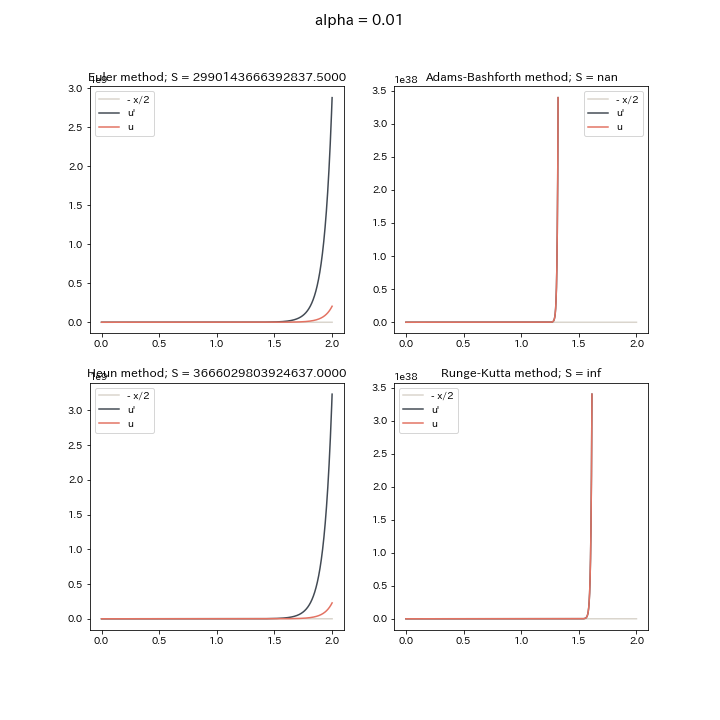
結果は次のようになりました。 グラフの名前に, 常微分方程式を使用したときのメソッド名と, その解軌跡における問題1に対応する面積を書いています。初期条件なしの最適解$u(x) = -\frac{x}{2}$の場合, 積分値は$-1$になるため, $\alpha$の絶対値を小さくすればするほど, この値に近づくはずです。
となり, 早速, 解が発散してしまいました。面積$S$も, どえらいことになっていますね。色々試した結果$\alpha > 0$のときは, 初期条件を$u(0) = 0, u'(0) = -\frac{1}{2}$とすると, $u = -\frac{x}{2}$の直線になり, そこから少しずらしただけで, 解が発散するため $\alpha > 0$だと不安定解になると予想されます。
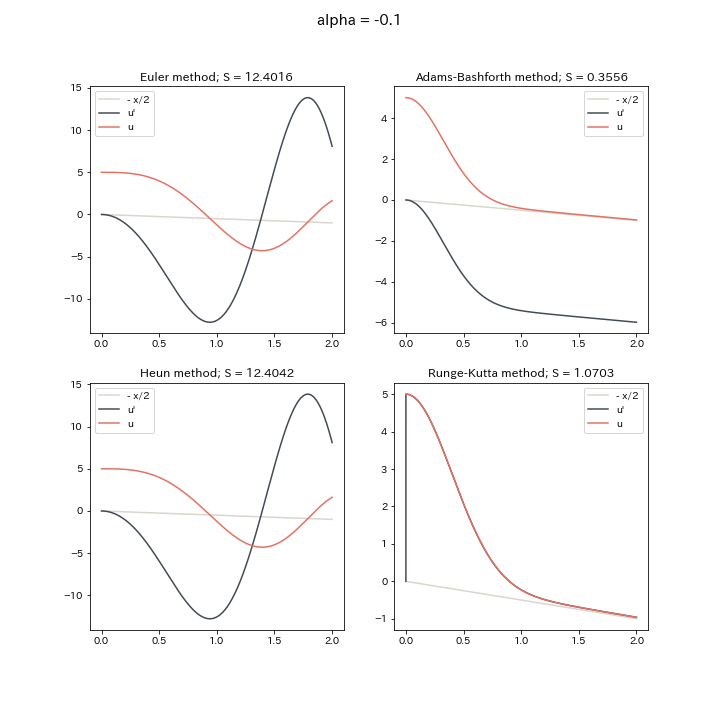
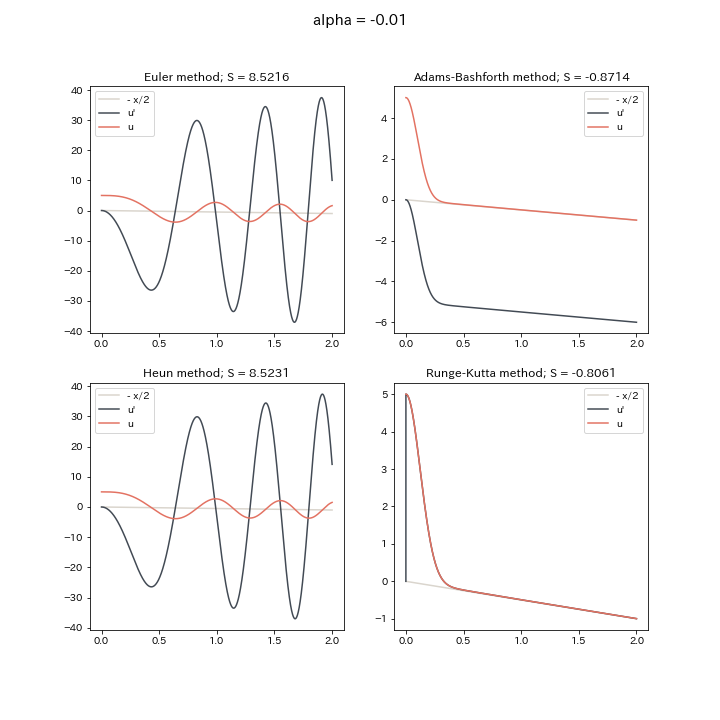
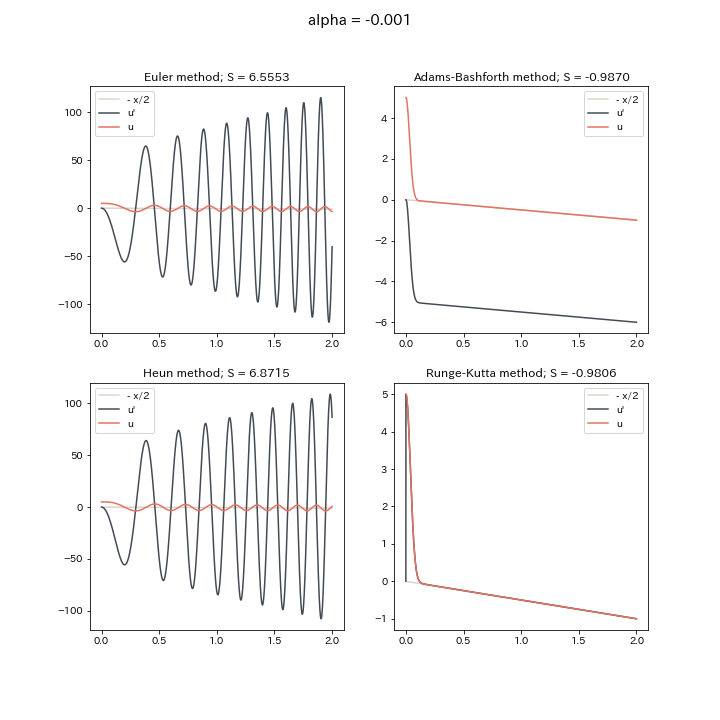
$\alpha < 0$の場合の計算例は
となっており, $\alpha < 0$のときは, 初期条件を変えてもこのような形に近づくため, 安定解であることが予想されます。 $\alpha$の絶対値が小さくなるほど$u = -\frac{x}{2}$に近づいていることや, 問題3の形から, $\alpha$の絶対値が小さくなるについて$u'$の増減が大きくなっていることも見てとれます。 また計算手法は, この場合はAdams-BashforthとRunge-Kuttaが特に優れていることがわかりますね。
問題例4(境界条件(初期条件+終端条件)あり)
F(x, u(x)) = x^2u(x) + xu(x)^2 + \alpha u'(x)^2\\
\displaystyle {\rm Minimize}\,\,\,\int_{a}^{b}F(x, u(x))\\
{\rm s.t.}\,\,\,\,\,\,\,\,u(a) = u_a,\,\,u(b) = u_b
最後に終端条件も追加された場合を考えてみましょう。 まず, オイラー・ラグランジュ方程式より
F_u - \frac{d}{dx}F_{u'} = 0 \iff u'' = \cfrac{1}{2\alpha}(x^2 + 2xu) \cdots (i)
が導かれます。これは問題3と同じですね。これについて
u'' \approx \cfrac{u(x-h)-2u(x)+u(x+h)}{h^2}\,\,\,\,(hは十分小さい)
と近似します。それを$(i)$に代入すると,
u(x-h)-2u(x)+u(x+h) = \cfrac{h^2}{2\alpha}(x^2 + 2xu(x))\\
\iff u(x-h)+(-2-\cfrac{1}{\alpha}h^2x)u(x)+u(x+h) = \cfrac{h^2}{2\alpha}x^2
これより, $[a, b]$を$a = x_0 < x_1 < \ldots < x_N = b$と$N+1$等分割すると
\begin{cases}
u(x_{n-1})+(-2-\cfrac{1}{\alpha}h^2x_n)u(x_n)+u(x_{n+1}) = \cfrac{h^2}{2\alpha}x_n^2\,\,\,(n = 1, \ldots, N-1)\\
u(x_0) = u_a\\
u(x_N) = u_b
\end{cases}
という連立方程式が得られます。行列の形で整理をすると
\begin{bmatrix}
1 & 0 & 0 & \cdots & 0 & 0\\
1 & -2-\frac{1}{\alpha}h^2x_1 & 1 & \cdots & 0 & 0\\
0 & 1& -2-\frac{1}{\alpha}h^2x_2 & \cdots & 0 & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & -2-\frac{1}{\alpha}h^2x_{N-1} & 1 \\
0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix}
\begin{bmatrix} u_0 \\ u_1 \\ u_2 \\ \vdots\\ u_{N-1} \\ u_N \end{bmatrix}
= \begin{bmatrix} u_a \\ \frac{h^2}{2\alpha}x_1^2 \\ \frac{h^2}{2\alpha}x_2^2 \\ \vdots\\ \frac{h^2}{2\alpha}x_{N-1}^2 \\ u_b \end{bmatrix}
となります。あとはこれを解けばいいですね。
from scipy.sparse import lil_matrix
A = lil_matrix((N, N), dtype='float32') # 疎行列として定義
# 行列の作成
A[0, 0] = A[N-1, N-1] = 1
for i in range(1, N-1):
A[i, i-1] = A[i, i+1] = 1
A[i, i] = -2-h**2*T[i]/alpha
A = A.tocsr()
# ベクトル(右辺)の作成
b = np.matrix([0 for _ in range(N)], dtype='float32').T
b[0] = U[0, 0] # 初期条件
b[N-1] = U[N-1, 0] # 終端条件
for i in range(1, N-1):
b[i] = (h*T[i])**2/(2*alpha)
scipyの疎行列を用いて行列を作成します。(numpyのmatrixだと死ぬほど遅い)
from scipy.sparse.linalg import spsolve
x = spsolve(A, b) # 連立方程式を解く
y = np.squeeze(np.asarray(x)) # 結果の取り出し
結果は以下の通りです。
$[a, b] = [0, 2], u_a = 2, u_b = 1$と設定しています。
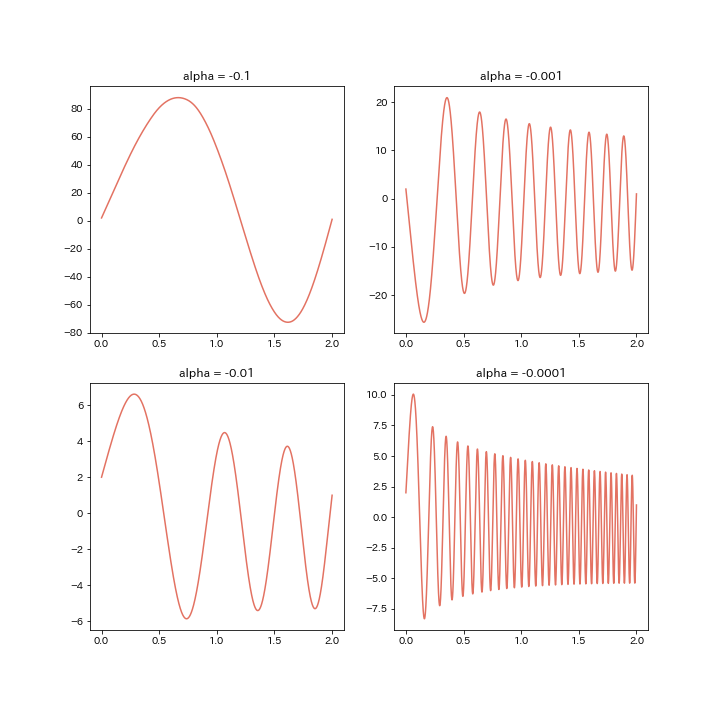
$\alpha$が負ですが, すごく振動していますね。次は$\alpha$を正にして計算した結果です。
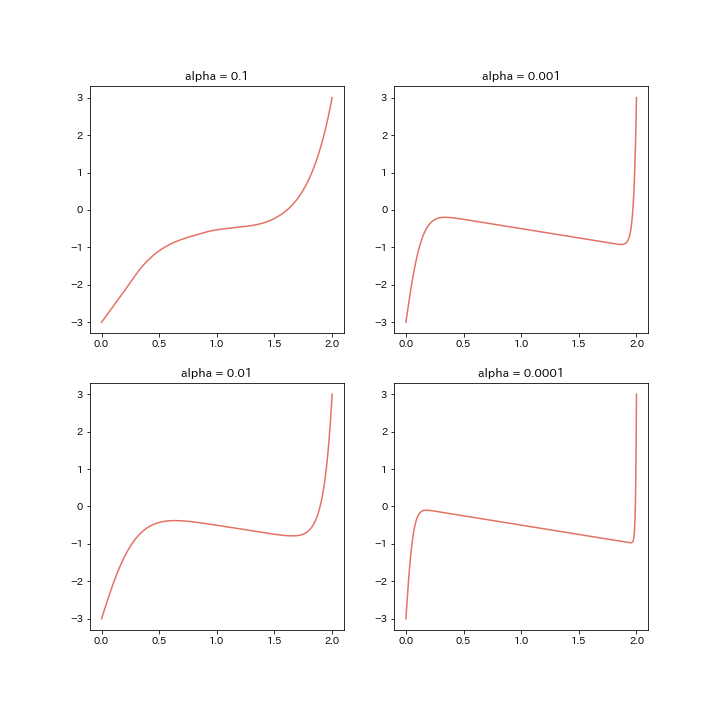
今回は, $\alpha$が正の方が解が安定していますね。(何故だ?!)
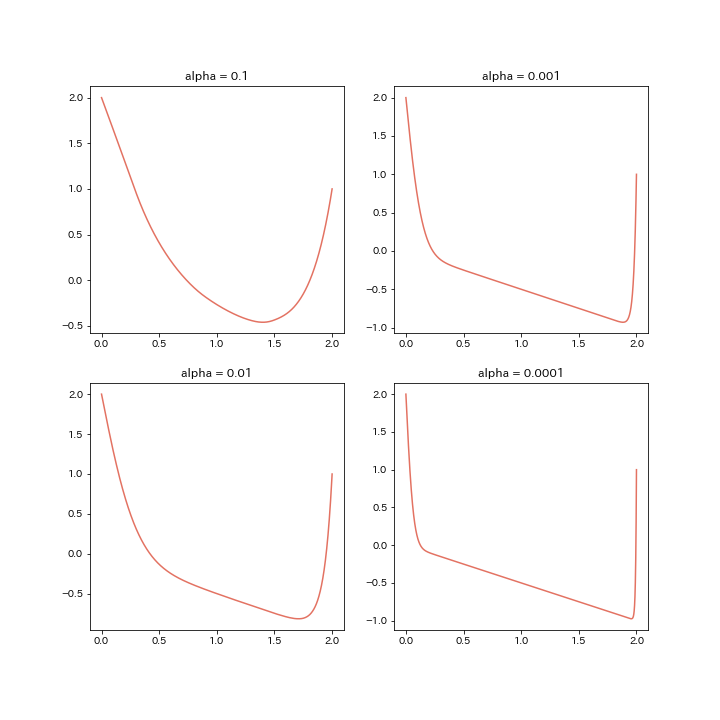
$[a, b] = [0, 2], u_a = -3, u_b = 3$としたときの結果も載せておきます。
$\alpha$が小さくなるほど, 関数が滑らかでなくなり, $-\frac{x}{2}$に近づいていることがわかります。
まとめ
以上, 簡単な問題を例に一通り変分問題を解いていきました。変分問題は, 紹介したものより多くの応用があります(動き得る境界を持つ場合, 拘束条件が付つ場合など)。より詳しく知りたい方は 少し古い本ですが[7][L.E.エルスゴルツ, 科学者・技術者のための変分法. (瀬川富士訳)] [8][L.E.エルスゴルツ, 科学者・技術者のための変分法 <<学習指導書>>. (富久泰明編集)]がオススメです。(絶版なので, 大学などの研究機関の図書館にしか置いてないかもしれません)
参考
[1] 変分法, https://ja.wikipedia.org/wiki/変分法
[2] 第6章 変分問題, http://www2.kaiyodai.ac.jp/~yoshi-s/Lectures/Optimization/2013/lecture_6.pdf
[3] 変分法の入門編, http://minami106.web.fc2.com/math/henbun2.pdf
[4] 寒野善博, 土屋隆, 最適化と変分法. 丸善出版, 東京, p233-p274 (2014)
[5] 齊藤宣一, 数値解析入門 初版. 東京大学出版会, 東京, p209-pp252, (2012)
[6] 常微分方程式(初期条件あり)の数値解析による解軌跡の導出, https://qiita.com/nariaki3551/items/c94462307c47af0da65b
[7] L.E.エルスゴルツ, 科学者・技術者のための変分法. (瀬川富士訳), ブレイン図書出版株式会社, 東京, (1979)
[8] L.E.エルスゴルツ, 科学者・技術者のための変分法 <<学習指導書>>. (富久泰明編集), ブレイン図書出版株式会社, 東京, (1981)
スクリプト
参考までに今回グラフを作成するのに用いたスクリプトです。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import lil_matrix
from scipy.sparse.linalg import spsolve
def f(t, u):
return (t*t + 2*t*u) / (2*alpha)
def g(t, u):
return t*t*u + t*u*u
def cal_area(U):
S = 0
for i, t in enumerate(T[:-1], 1):
S = S + h * (g(t-h, U[i-1, 0]) + g(t, U[i, 0])) / 2
return S
a = 0 # 始点
b = 2 # 終点
N = 10000 # 区切り数
alpha = -0.01 # パラメータ
T, h = np.linspace(a, b, num=N, retstep = True) # h 区切り幅
U = np.array([[0, 0] for _ in range(N)], dtype='float32') # U[:, 0] u, U[:, 1] u'
U[0, 0] = 5 # u の aでの値
U[0, 1] = 0 # u' の aでの値
U[N-1, 0] = 3
def plot_fig(ax, U, method):
ax.plot(T, -T/2, label="- x/2", color='#dad5cd')
ax.plot(T, U[:, 1], label="u'", color='#424a54')
ax.plot(T, U[:, 0], label="u", color='#e37262')
ax.set_title(method)
ax.legend()
fig, ax = plt.subplots(2, 2, figsize=(8, 8))
# Euler method
for i, t in enumerate(T[1:], 1):
U[i] = U[i-1] + [h*U[i-1, 1], h*f(t-h, U[i-1, 0])]
S = cal_area(U)
plot_fig(ax[0, 0], U, f'Euler method; S = {S:0.4f}')
# Heun法
for i, t in enumerate(T[:-1], 1):
delta = np.array([U[i-1, 1], (f(t-h, U[i-1, 0]) + f(t, U[i-1, 0]+h*f(t-h, U[i-1, 0]))) / 2])
U[i, :] = U[i-1, :] + h*delta
S = cal_area(U)
plot_fig(ax[1, 0], U, f'Heun method; S = {S:0.4f}')
# Adams-Bashforth method
for i, t in enumerate(T[:-1], 1):
if i == 1:
U[i] = U[i-1] + h*(f(t-h, U[i-1, 0]) + f(t, U[i-1]+h*f(t-h, U[i-1, 0]))) / 2
else:
U[i] = U[i-1] + h*(3*f(t-h, U[i-1, 0]) - f(t-2*h, U[i-2, 0])) / 2
S = cal_area(U)
plot_fig(ax[0, 1], U, f'Adams-Bashforth method; S = {S:0.4f}')
# Runge-Kutta method
for i, t in enumerate(T[:-1], 1):
k1 = f(t-h, U[i-1, 0])
k2 = f(t-h/2, U[i-1, 0]+h*k1/2)
k3 = f(t-h/2, U[i-1, 0]+h*k2/2)
k4 = f(t, U[i-1, 0]+h*k3)
U[i] = U[i-1, 0] + h*(k1 + k2 + k3 + k4) / 6
S = cal_area(U)
plot_fig(ax[1, 1], U, f'Runge-Kutta method; S = {S:0.4f}')
fig.suptitle(f'alpha = {alpha}', fontsize=15)
plt.show()
# plt.savefig('ode0.01.png')
def solve_eq(N, U, T, h, alpha):
""" Solve the equation Ax = b for x """
A = lil_matrix((N, N), dtype='float32')
A[0, 0] = A[N-1, N-1] = 1
for i in range(1, N-1):
A[i, i-1] = A[i, i+1] = 1
A[i, i] = -2-h**2*T[i]/alpha
A = A.tocsr()
b = np.matrix([0 for _ in range(N)], dtype='float32').T
b[0] = U[0, 0] # 初期条件
b[N-1] = U[N-1, 0] # 終端条件
for i in range(1, N-1):
b[i] = (h*T[i])**2/(2*alpha)
x = spsolve(A, b)
y = np.squeeze(np.asarray(x))
U[:, 0] = y
return U
fig, ax = plt.subplots(2, 2, figsize=(8, 8))
ax[0, 0].plot(T, solve_eq(N, U, T, h, -0.1)[:, 0], label="u", color='#e37262')
ax[1, 0].plot(T, solve_eq(N, U, T, h, -0.01)[:, 0], label="u", color='#e37262')
ax[0, 1].plot(T, solve_eq(N, U, T, h, -0.001)[:, 0], label="u", color='#e37262')
ax[1, 1].plot(T, solve_eq(N, U, T, h, -0.0001)[:, 0], label="u", color='#e37262')
ax[0, 0].set_title('alpha = 0.1')
ax[1, 0].set_title('alpha = 0.01')
ax[0, 1].set_title('alpha = 0.001')
ax[1, 1].set_title('alpha = 0.0001')
plt.show()