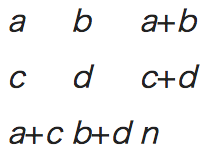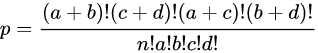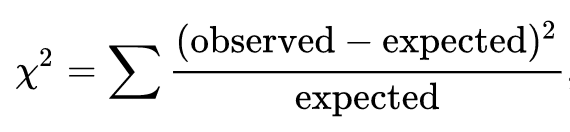chi二乗検定と、fisherの正確検定
chi二乗検定と、fisherの正確検定について知見と使い方とか
自分のなかで幾つかの幾何学的に導ける検定とが正規分布とかガウシアンなんとかをいい加減にまとめようと思いました。
fisherの正確検定
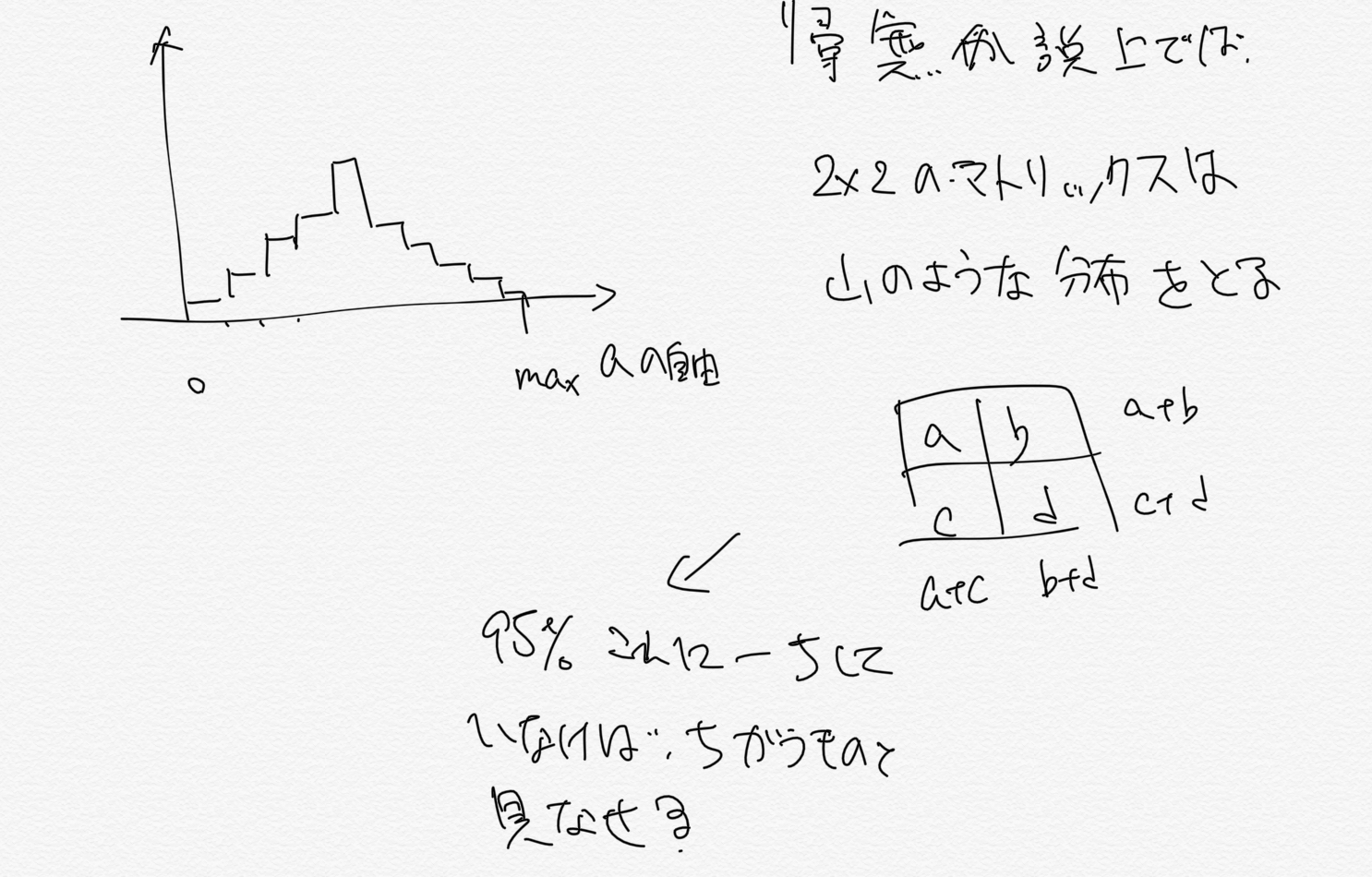
考え方としては、一個一個のマトリックスの事象が”平等に起こり得る”という帰無仮説を立てると、次のように簡単に組み合わせ表現にすることができます
例として2x2の4つの目を仮定します
ある組み合わせが起こりうる頻度を表すとこのようになります
これをpythonでコーディングするとこのようになる
import math
# web良かった、web悪かった, SI良かった, SI悪かった
a,b,c,d = [5,1,1,6]
ps = []
for a in range(0, 6 + 1):
b = 6 - a
c = 6 - a
d = 7 - b
ps.append( (a,b,c,d) )
s = math.factorial( a+b ) * \
math.factorial( a+c ) * \
math.factorial( b+d ) * \
math.factorial( c+d ) / ( math.factorial(a) * \
math.factorial(b) * \
math.factorial(c) * \
math.factorial(d) * math.factorial(a+b+c+d) )
print(a, s)
print(ps)
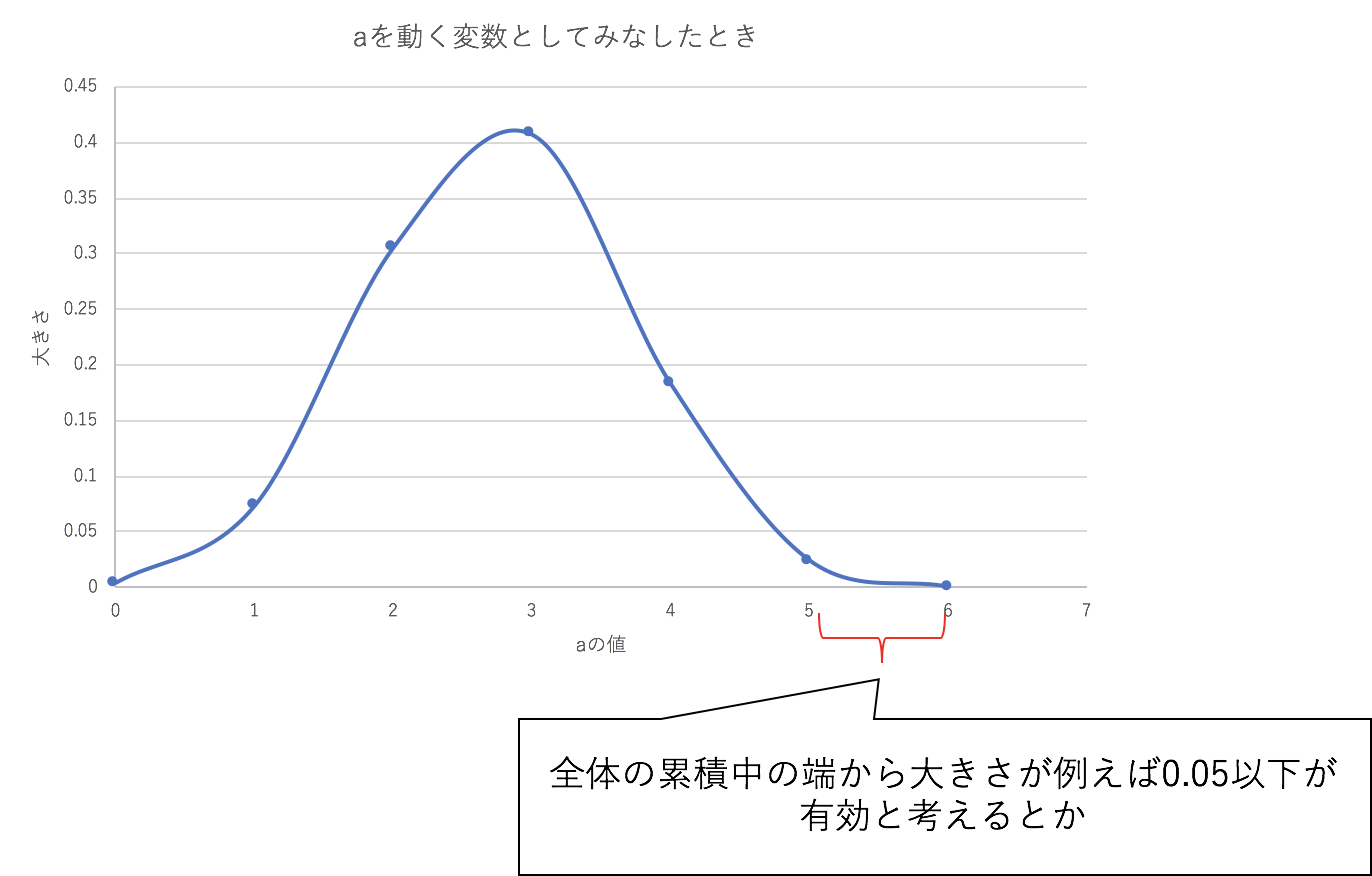
これを行うと山状の形を自由度に応じて得ることができて、山の面積の95%以外にあればそれは自然に起きたことではないという解釈が成り立ちそう
これをもってして何が言えるかというしてん視点では、なにかしらバイアスがあっていい悪いsi, webの選択が平等に起こり得るという状態が否決されたと見させそうです（例えばweb, siの差を論じるたぐいの解釈は難しいです）
考え方としてシンプルで私は好きなのですが、後述のchi二乗検定に比べるとあまり流行っていないように見受けられます(そもそも事象同士を比べるものではないかかでしょうか)
chi二乗検定
あるあるの検定で最も簡単にできます
サイコロを具体例にとって説明すると、カイ二乗は、理論的な期待値（すべてのサイコロの目が平等にでる）から、観測された頻度の期待値（実際になんの目が何回でたかなど）の累積の誤差を求める作業と等価に見えます
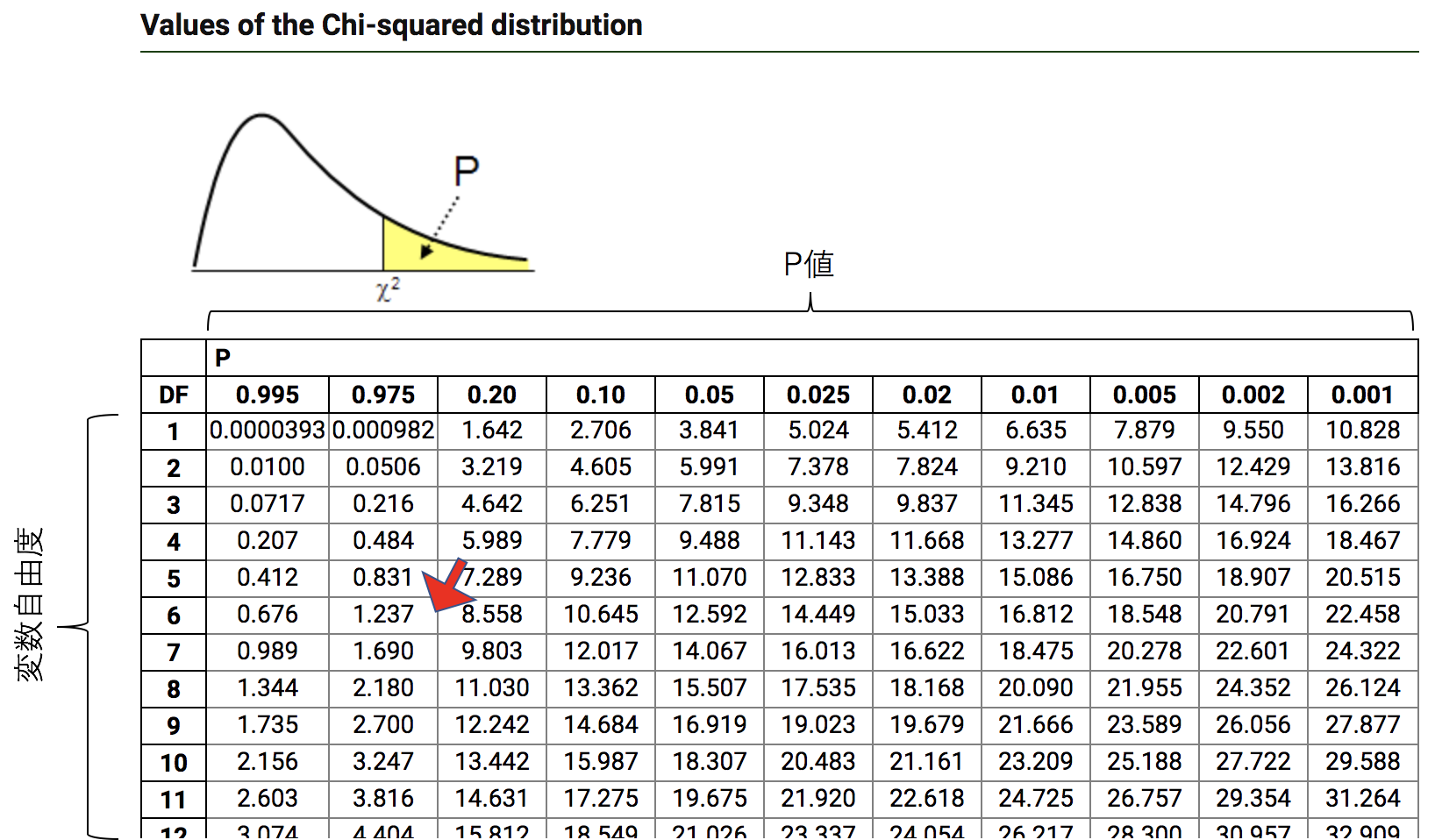
このような観測があった場合、例えばx^2は3.19となり、x^2分布をみると、下図のこの辺に位置しており全然中央に近い値なので、差はない（つまり自然なサイコロである）と言えそうです
現実的にはカイ二乗分布とよばれる表と対応させて調べるのは大変なので、ライブラリに隠蔽された状態で扱うのですが、例えばPythonでのサイコロの検定はこんな感じで、とても簡単にできます
(ランダム関数で、1000回適当にサイコロを回しています)
from scipy import stats
import random
from collections import Counter
observed = []
for i in range(1000):
x = random.choice([x+1 for x in range(6)])
observed.append(x)
observed = [freq for me, freq in sorted(dict(Counter(observed)).items(), key=lambda x:x[1]) ]
print(observed)
expected = [1000*1/6 for i in range(6)]
print(expected)
chisq,p = stats.chisquare(observed,expected)
print(f'chisq {chisq}')
print(f'p-val {p}')
おまけ
導出や理解をするにあたってしたことを雑にまとめています
fisher's exact
chi二乗検定
fisher's exactのような考え方を持ち込むことも可能なようにおもっていて（かなり無理くり感がありますが.）、DF(動かせる変数)を少しずつ全部見てその和をとり、chi二乗分布の表との見比べでp値を算出しますが、かりに、⊿が何かの絶対値でとある分布が取りにくいことを別の事象として定義するならば、これらの差のfisher's exactを算出しても意味があるものとなるかと思います(小並)