Project EulerにGaucheで挑戦する話

Lisp Advent Calendar 19日目担当の @naoya_t です。

「昨晩@g000001さんと回転寿司屋でLispについて話した」（※実話）とかでもいいんですが、予告通りProject Eulerの話を書こうと思います。

ちょっと投稿が遅くなりましたが、インド標準時（UTC+05:30；日本時間より3時間半遅れています）でぎりぎり19日ということでお許しください。

はじめに

本記事では、特定の問題の解答や、それを導くプログラムはProject Eulerの参加規約に抵触するため掲載しません。

Project Eulerとは

偉大な数学者レオンハルト・オイラーの名を冠するProject Eulerとはいったい何なのでしょうか？

英語版WikipediaでProject Eulerを開いてみると

Project Eulerは、コンピュータプログラムで解くことを意図した計算問題とそのジャッジメントシステムを提供するウェブサイトです。

数学やコンピュータプログラムに関心のある大人や学生が世界中から集まっています。
2012年12月19日（本稿執筆時点）現在で406問が掲載されています
難易度はさまざまですが、いずれも効率的なアルゴリズムを用いればそこそこのパワーがあるマシンなら１分もかからずに解ける問題です（訳注：まじっすか）。正答にたどり着いたら、各問専用のフォーラムでの議論に参加できます。

世界中から注目を集め、2001年にColin Hughesがサイトを発足して以来、約26万人のユーザが訪れています。

参加者は、正答問題数に基づいた15段階の達成レベルで自分の能力向上を見ることができます。
新しく参加したメンバーが昔の問題を解かなくても競えるように、Eulerianレベルというのも設けられていて、これは直近の幾つかの問題を最初に解いた20人に基づいています。

Project Eulerの問題のいくつかが、APLベンダーの１つDyalogが開催したAPLプログラミングコンテストで用いられました。
整数列オンライン百科事典(the On-Line Encyclopedia of Integer Sequences(OEIS))では、現在68の数列がProject Eulerの問題を参照しています。

（naoya_t抄訳）と説明されています。

回答欄に答えの数値を入力し、それが正解かどうかしか見ていない（=回答に至るプログラムないしスクリプトの提出は不要）ので、プログラミング言語は何を使っても構いません。Pencil/Paper(鉛筆と紙)での参戦も可能です。
※2012年12月19日現在、Schemerは「鉛筆と紙」勢に負けています。

データ：Project Euler と Scheme

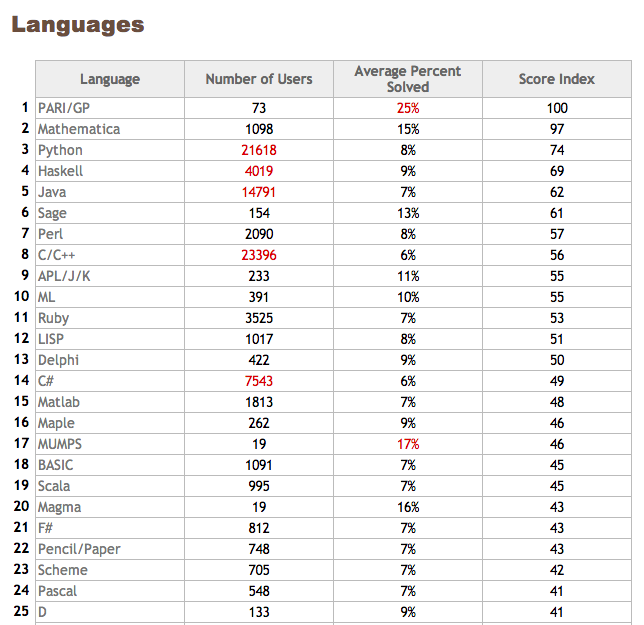
http://projecteuler.net/languages (要ログイン) によると…

• Schemeでの参加者は705名、正答率が7% → Project Euler全体の23位
• Pencil/Paper22位に負けてます＞＜
• 上位5言語はPARI/GP, Mathematica, Python, Haskell, Java
• ちなみにLISPが1017人/8%, Clojureが842名/6%
  

naoya_t個人成績（2012年12月19日現在）

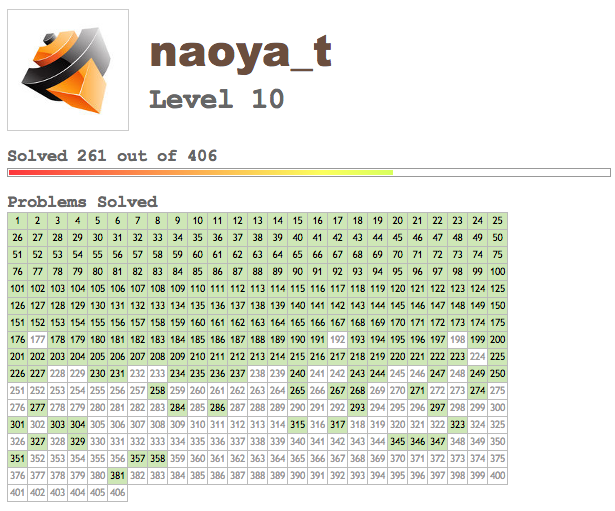
↑虫食い状態になっているのは212/220問まで解いた後３年半ブランクが空いた→今年の春頃に暇を持て余してた時に何問かつまみ食いしたためです。

• 406問中261問正答
• 日本からの参加者2180名中、naoya_t現在23位 http://projecteuler.net/country=Japan (要ログイン)
• Schemeでの参加者705名中では現在1位 http://projecteuler.net/language=Scheme (要ログイン)

最近時間（というか挑戦する気持ち）が割けなくて全然進んでいませんが、あと100問ぐらいは行けると思うのでそのうち何とかしたいです。

追記：Friend Keyは

4864086150836_7abbecb3db29e56be631729040879af9

です。フレンドうぇるかむです。

問題を解いてみよう

素数を生成する手段・素因数分解関数は必須

3〜4千万までの素数があれば大抵は事足ります。まずはエラトステネスのふるいを実装しましょう。
計算済みの素数データを用意しておいてmmapで読み込む、という方法も良いと思います。（heruさんの「Gaucheからmmapを使ってみる」シリーズ参照）

素数判定関数もあると良いですね。素数表がメモリにあるならそれを使うのも良いですし、Miller-Rabinテスト（SICP 1.28参照）等を実装しておくのも良いです。

素数だけでなく、与えられた整数を素因数分解する関数なども用意しておくと捗ります。
素因数分解ができたら、ついでにオイラーのφ関数(phi function, totient function)も知っていると便利です。これは、1からnまでの自然数のうち、nと互いに素なものの個数を表す関数で、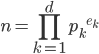と因数分解できるとき
で求めることができます。

よく使う関数

• 整数12345を(1 2 3 4 5)のようなリストに変換する、あるいはその逆
• 組み合わせの数 nCk を求める関数
• ピタゴラス数を余さず生成する関数
  シンプルな行列式で次々とピタゴラス数を生成する行列があるのでこれを利用すると良いです。「ピタゴラス数を生み出す行列のはなし」という本がお勧めです。

使ってるライブラリの一部を晒してみます。

euler.scm

(use srfi-1)
(use util.combinations)
(use gauche.uvector)

(define pi 3.141592653589793238462643383279)
(define phi (/ (+ 1 (sqrt 5)) 2))

(define *log2* (log 2))
(define *log10* (log 10))

(define (log2 x) (/ (log x) *log2*))
(define (log10 x) (/ (log x) *log10*))

;(use math.mt-random)
;(define *mt* (make <mersenne-twister> :seed (sys-time)))
;(define (rand100) (mt-random-integer *mt* 100))

#|
VECTOR
|#

(define (vector-inc! v ref d)
  (vector-set! v ref (+ (vector-ref v ref) d)))

#|
MATH
|#

(define (divisible? x y) (zero? (remainder x y)))
(define (sum lis) (apply + lis))
(define (prod lis) (apply * lis))
(define (square x) (* x x))
(define (cube x) (* x x x))

(define (digits base n)
  (if (= n 0) (list 0)
      (let loop ((n n) (s '()))
        (if (= n 0) (reverse! s)
            (receive (q r) (quotient&remainder n base)
              (loop q (cons r s)))))))

#|
COMBINATIONS
|#

(define (C n k)
  (let loop ((x 1) (n n) (k (min k (- n k))))
    (if (= k 0) x
        (loop (/ (* x n) k) (- n 1) (- k 1)))))

(define (xrange a b) (iota (- b a -1) a))

#|
PRIMES

(define primes (do-sieve 2500000)) ; 10sec for 25000000
(print (length primes))
(exit)
;(define primes '(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79))
|#

(define sieve #())
(define (prime? n) (vector-ref sieve n))

(define (_prime? n primes)
  (let loop ((ps primes))
    (if (null? ps) #t
        (if (divisible? n (car ps)) #f
            (loop (cdr ps))))))

(define (do-sieve M)
  (define (elim n)
    (let loop ((i (* n 2)))
      (if (<= i M)
          (begin
            ;(s32vector-set! sieve i 1)
            (vector-set! sieve i #f)
            (loop (+ i n)))
          #t)))

  (set! sieve (make-vector (+ M 1) #t))

  (display "do sieve 2..") (flush)
  (vector-set! sieve 0 #f)
  (vector-set! sieve 1 #f)
  (elim 2)
  (let loop ((n 3) (ps (list 2)))
    (if (<= n M)
        (loop (+ n 2)
              (if (prime? n)
                  (begin
                    (elim n)
                    (cons n ps))
                  ps))
        (begin
          (print "M. done.")
          (reverse! ps)))))

(define (prime-factors->divisors pf) ;; '(2 1 1) -> 
  (define (pfs p n) ; --> (p^n p^(n-1) ... p^2 p 1)
    (let loop ((i 0) (p^i 1) (ls '()))
      (if (> i n) ls
          (loop (+ i 1) (* p^i p) (cons p^i ls)))))
  (let loop ((pf pf) (ps primes) (ls '()))
    (if (null? pf)
        (map (cut apply * <>) (cartesian-product ls))
        (loop (cdr pf) (cdr ps)
              (if (zero? (car pf)) ls
                  (cons (pfs (car ps) (car pf)) ls) )))))

(define (prime-factors n)
  (let lp1 ((n n) (ps primes) (ls '()))
    (if (= 1 n) (reverse! ls)
        (let1 p (car ps)
          (let lp2 ((n n) (i 0))
            (if (divisible? n p)
                (lp2 (/ n p) (+ i 1))
                (lp1 n (cdr ps) (cons i ls))))))))

(define (pf-nums pf)
  ;(filter identity (map (lambda (p) (if (zero? (car p)) #f (cadr p))) (zip pf primes))))
  (let loop ((pf pf) (ps primes) (ls '()))
    (if (null? pf) (reverse! ls)
        (loop (cdr pf) (cdr ps) 
              (if (zero? (car pf)) ls (cons (car ps) ls))))))

(define (pf-test n)
  (let1 pf (prime-factors n)
    (print "prime factors of " n " = " (pf-nums pf))
    (print "divisors of " n " = " (sort (prime-factors->divisors pf)))))

(define (pf-merge pf1 pf2)
  (let loop ((pf1 pf1) (pf2 pf2) (pf '()))
    (cond ((null? pf1) (append (reverse! pf) pf2))
          ((null? pf2) (append (reverse! pf) pf1))
          (else (loop (cdr pf1) (cdr pf2) (cons (+ (car pf1) (car pf2)) pf))))))

(define (next-prime n)
  (let loop ((x (+ n 1)))
    (if (even? x) (loop (+ x 1))
        (let1 sq (floor->exact (sqrt x))
          (let lp ((ps primes))
            (if (null? ps) x
                (let1 p (car ps)
;             (if (> p sq) x
                  (if (divisible? x p) (loop (+ x 2))
                      (lp (cdr ps))))))))))

(define (totient k)
  (let loop ((x k) (pfn (pf-nums (prime-factors k))))
    (if (null? pfn) x
        (loop (* x (- 1 (/ (car pfn)))) (cdr pfn)))))

#|
FIBONACCI
|#

#;(define fib-ht (make-hash-table 'eq?))
#;(define (fib n)
  (cond ((= n 1) 1)
        ((= n 2) 2)
        (else
         (or (hash-table-get fib-ht n #f)
             (let1 val (+ (fib (- n 1))
                          (fib (- n 2)))
               (hash-table-put! fib-ht n val)
               val)) 
         )))

;; USING MATRIX
(define (fib n)
  (define (M x) (remainder x 1234567891011))

  (define (A* A B)
    (cons (cons (M (+ (* (caar A) (caar B))
                      (* (cdar A) (cadr B))))
                (M (+ (* (caar A) (cdar B))
                      (* (cdar A) (cddr B)))))
          (cons (M (+ (* (cadr A) (caar B))
                      (* (cddr A) (cadr B))))
                (M (+ (* (cadr A) (cdar B))
                      (* (cddr A) (cddr B)))))))
  (define (A** A) (A* A A))

  (define A-ht (make-hash-table 'eq?))
  (define A1 (cons (cons 1 1) (cons 1 0)))
  (define (An n)
    (if (= n 1) A1 ;; aa da ad dd
        (or (hash-table-get A-ht n #f)
            (let1 v (if (even? n)
                        (A** (An (/ n 2)))
                        (A* (An (- n 1)) A1))
              ;(format #t "(An ~d)..\n" n)
              (hash-table-put! A-ht n v)
              v))))

  (if (= n 0) 0
      (M (cdar (An n)))))

#|
PYTHAGOREAN
|#

(define (py3 a b c)
  (define (U a b c)
    (list (+ (* a 1) (* b -2) (* c 2))
          (+ (* a 2) (* b -1) (* c 2))
          (+ (* a 2) (* b -2) (* c 3))))
  (define (A a b c)
    (list (+ (* a 1) (* b 2) (* c 2))
          (+ (* a 2) (* b 1) (* c 2))
          (+ (* a 2) (* b 2) (* c 3))))
  (define (D a b c)
    (list (+ (* a -1) (* b 2) (* c 2))
          (+ (* a -2) (* b 1) (* c 2))
          (+ (* a -2) (* b 2) (* c 3))))

  (values (U a b c) (A a b c) (D a b c)))

(define pytagoreans (make-hash-table 'equal?))
(define (make-pytagoreans upper)
  (let loop ((tr '(3 4 5)))
    (when (every (cut <= <> upper) tr)
      (hash-table-put! pythagoreans tr #t)
      (receive (u a d) (apply py3 tr)
        (loop u) (loop a) (loop d) ))))

繰り返し

letを用いて

(let loop ((l lis) (i 0))
  . . .
  )

のようなループを書くことが多いです。（末尾再帰になるように気をつけましょう！）
foldはちょっと遅い印象があってあまり使いません（※Gauche 0.9.3からfoldがコアでサポートされたので改善されてるかもです。）が、やはり簡潔に書けるのでたまに使います。

forループ的な事をしたい時にはScheme純正のdo文も使いますが、dotimesで済む時はdotimesだったりします。これはCommon Lispから導入されたマクロですね。

ハッシュテーブル

make-hash-table hash-table-get hash-table-put! あたりには非常にお世話になっています。
時々GCが悲鳴をあげるのを聞くことができます。

大きな整数（Bignum）をキーにする場合、比較関数にはeq?ではなくeqv?を使う、という点は（言語実装を考えると自明かもしれませんが）忘れがちなので要注意です。

おわりに

１人でも多くのSchemerがProject Eulerに参加し、「黒板言語」の宿敵「鉛筆と紙」勢を打ち破ることができたら嬉しいです。

ところで、休眠中だったShibuya.lispが、運営スタッフを世代交代し動き出そうとしています。
有志運営スタッフ（naoya_t含む）によるブートストラップ・ミーティングが年明けに開かれる予定です。第2期はどんな感じになるんでしょうか。Tech TalkやLightning Talksで新しいネタが聞けるのを楽しみにしています。