AR(1)モデルの基本
AR(1)モデルは以下のように表される。
$$
X_t = \phi X_{t-1} + \epsilon_t
$$
ここで、$X_t$は時刻$t$での時系列の値、$\phi$は自己回帰係数、$\epsilon_t$は平均がゼ$0$で分散が $\sigma^2$ のホワイトノイズ誤差である。
また、定常性の条件$|\phi|<1$を仮定する。
AR(1)モデルの分散
$V[X_t]=\tau^2$とおくと、
$$\tau^2 = V[X_t]=\phi ^2[ X_{t-1}] + V[\epsilon_t] = \phi ^2\tau^2+\sigma^2$$より、
$$\tau^2=\frac{\sigma^2}{1-\phi ^2}$$が成り立つ。
AR(1)モデルの共分散
$X_t$と$X_{t+1}$の共分散は
$$Cov[X_t,X_{t+1}]=\phi V[X_t]=\frac{\sigma^2}{1-\phi ^2}\phi$$となる。同様に$X_t$と$X_{t+2}$の共分散は
$$Cov[X_t,X_{t+2}]=\phi \thinspace Cov[X_t,X_{t+1}]=\phi^2 V[X_t]=\frac{\sigma^2}{1-\phi ^2}\phi^2$$となる。この議論を繰り返し、定常性と合わせて
$$Cov[X_i,X_{j}]=\frac{\sigma^2}{1-\phi ^2}\phi^{|i-j|} $$を得る。
自己共分散関数と自己相関関数
時系列モデルでは
$$\gamma_t=Cov[X_0,X_{t}], \enspace \gamma_{|t-s|}=Cov[X_t,X_{s}]$$という様に表し、自己共分散関数と呼ぶことが一般的である。
また、
$$\rho_k=\frac{\gamma_k}{\gamma_0}$$をラグ$k$の自己相関関数と呼ぶ。
上記の式から、AR(1)モデルの場合、$\rho_1=\phi$が成り立っていることが分かる。
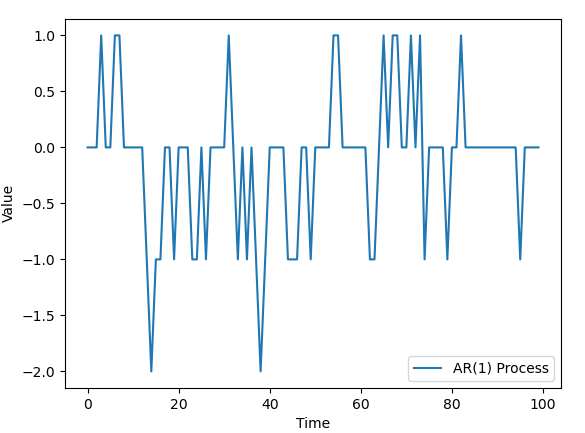
AR(1)モデルのコードの例
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
# ダミーデータの生成
np.random.seed(42)
nobs = 100
time = np.arange(nobs)
phi = 0.7 # AR(1)モデルのパラメータ
epsilon = np.random.normal(0, 1, size=nobs)
y = np.zeros_like(time)
# AR(1)モデルの構築
for t in range(1, nobs):
y[t] = phi * y[t-1] + epsilon[t]
# プロット
plt.plot(time, y, label='AR(1) Process')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()
# AR(1)モデルのフィッティング
model = sm.tsa.AR(y)
result = model.fit()
# パラメータの表示
print(result.summary())
ホワイトノイズの条件
$$E[\epsilon_t] = 0$$$$Cov[\epsilon_t,\epsilon_{s}]=0, t \neq s $$$$Var[\epsilon_t]=E[\epsilon_t^2] = \rm{const}$$