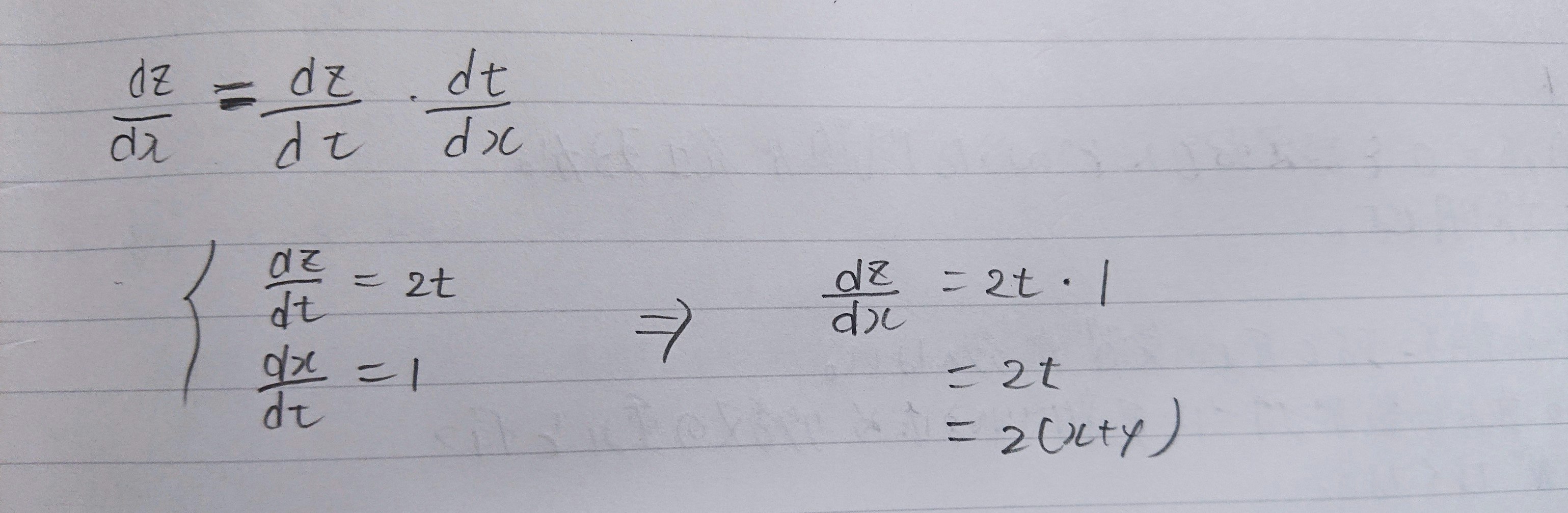#はじめに
本記事は、E資格の受験資格の取得を目的としたラビットチャレンジを
受講した際の勉強記録およびレポート記事である。
###連鎖律
■確認テスト
連鎖律の原理を使い、dz/dxを求めよ。
$z = t^2$
$t = x + y$
・解答
##Section1：勾配消失問題
誤差逆伝搬法が下位層に進んでいくにつれて、勾配がどんどん緩やかに
なっていく。そのため、勾配降下法による更新では下位層のパラメータは
ほとんど変わらず、訓練は最適値に収束しなくなる。
■確認テスト
シグモイド関数を微分したとき、入力値が0のときに最大値をとる。
その値として正しいものを選択肢から選べ。
(1)0.15
(2)0.25
(3)0.35
(4)0.45
・解答
###重みの初期値設定-Xavier
Xavierの初期値を設定する際の活性化関数
◆ReLu関数
◆シグモイド (ロジスティック) 関数
◆双曲線正接関数
###重みの初期値設定-He
Heの初期値を設定する際の活性化関数
◆ReLu関数
■確認テスト
重みの初期値に0を設定すると、どのような問題が発生するか。
簡潔に説明せよ。
・解答
重みを0で初期化すると正しい学習が行えない。
すべての重みの値が均一に更新されるため多数の重みをもつ意味がなくなる。
■確認テスト
一般的に考えられるバッチ正規化の効果を2点挙げよ。
・解答
計算量の高速化
勾配消失が起こりにくくなる
■例題
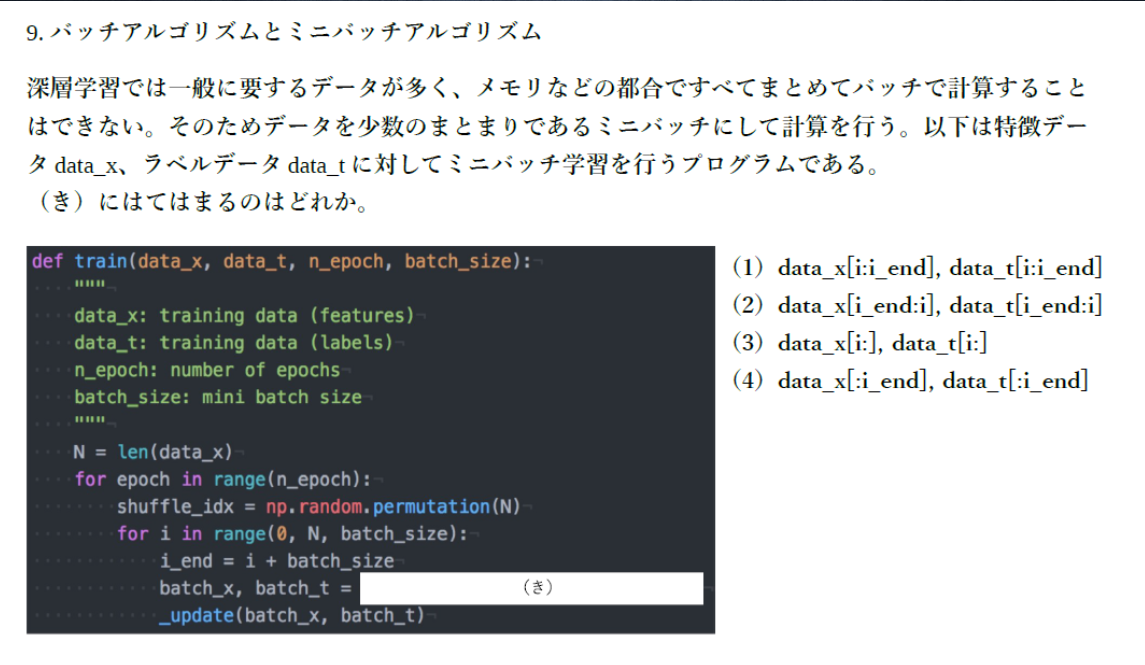
・解答
(1)。バッチサイズだけデータを取り出す処理。
■演習
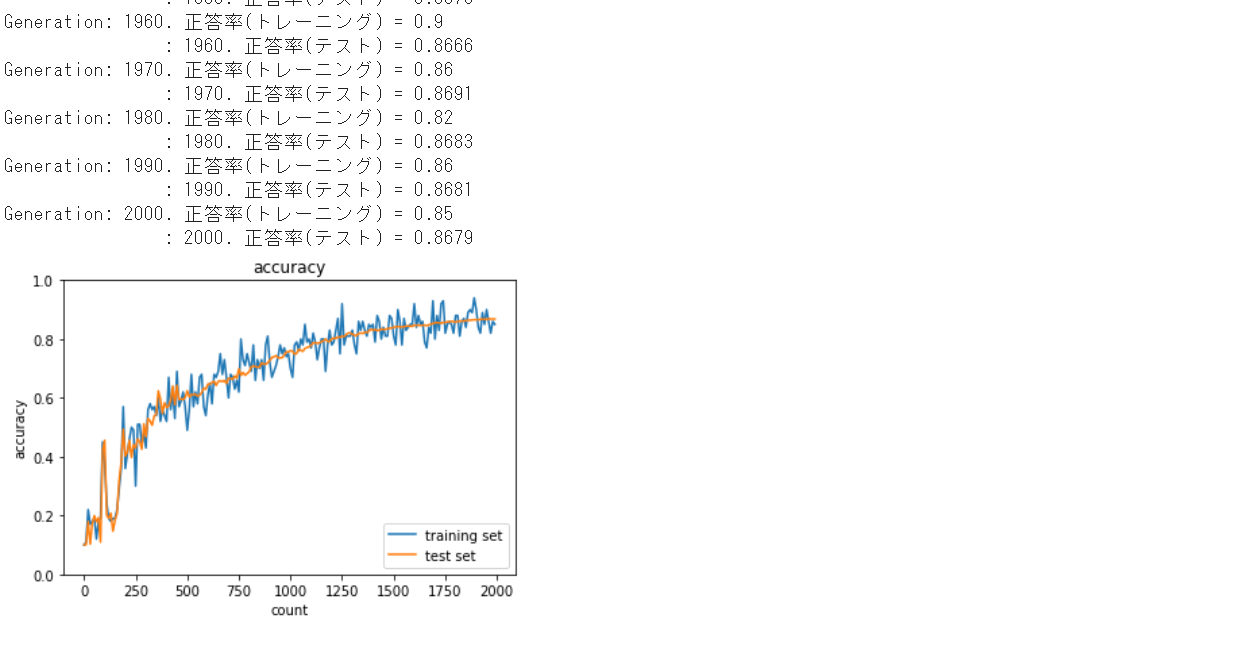
重みの初期化をガウス分布、活性化関数をシグモイド関数とすると
勾配消失問題が発生。この場合、活性化関数をReLU関数にすると
学習がうまく進んでいくことが確認された。
また活性化関数はシグモイド関数でXavier初期化をした場合、
勾配消失問題の発生はなく学習がうまく進んでいくことが確認された。
活性化関数ReLUでも学習がうまく進んでいく。
Xavier、Heでの重みの初期化は勾配消失問題を防ぐ有効な手段であること
が確認できた。
##Section2：学習率最適化手法
###モメンタム
◆メリット
・局所的最適解にはならず、大域的最適解となる。
・谷間についてから最も低い位置 (最適値) にいくまでの時間が早い
$V_t = \mu V_{t-1} -\epsilon \nabla E$
$\boldsymbol w^{(t+1)} = \boldsymbol w^{(t)}+V_t$
###AdaGrad
◆メリット
・勾配の緩やかな斜面に対して、最適値に近づける
◆課題
・学習率が徐々に小さくなるので、鞍点問題を引き起こす事があった
$h_0=\theta$
$h_t = h_{t-1}+(\nabla E)^2$
$\boldsymbol w^{(t+1)} = \boldsymbol w^{(t)} - \epsilon \frac{1}{\sqrt{h_t}+\theta} \nabla E$
###RMSProp
◆メリット
・局所的最適解にはならず、大域的最適解となる
・ハイパーパラメータの調整が必要な場合が少ない
$h_t = \alpha h_{t-1}+(1-\alpha)(\nabla E)^2$
$\boldsymbol w^{(t+1)} = \boldsymbol w^{(t)} - \epsilon \frac{1}{\sqrt{h_t}+\theta} \nabla E$
###Adam
・モメンタムの過去の勾配の指数関数的減衰平均
・RMSPropの過去の勾配の2乗の指数関数的減衰平均
上記をそれぞれ孕んだ最適化アルゴリズムである。
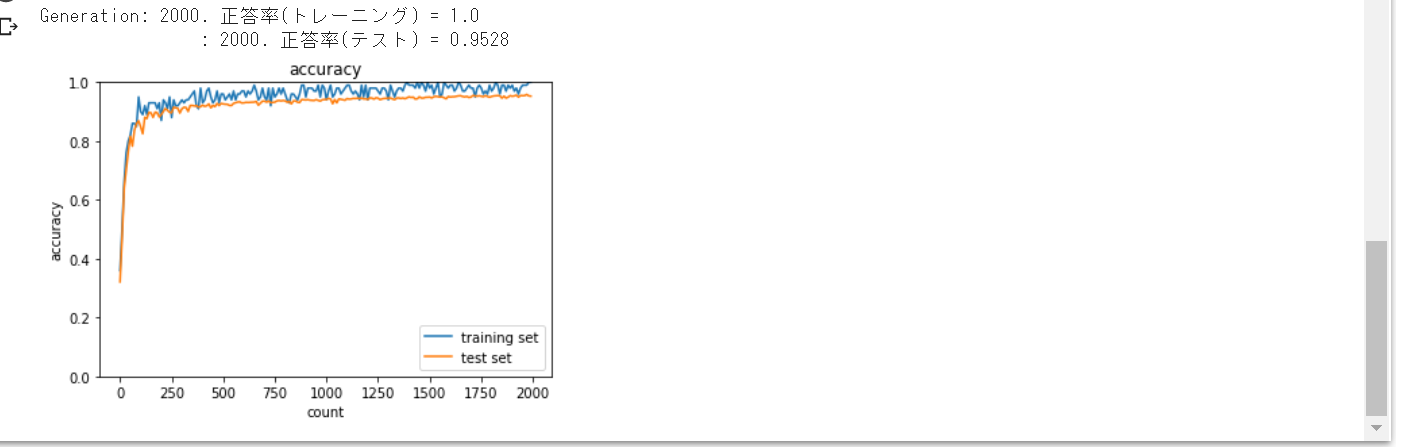
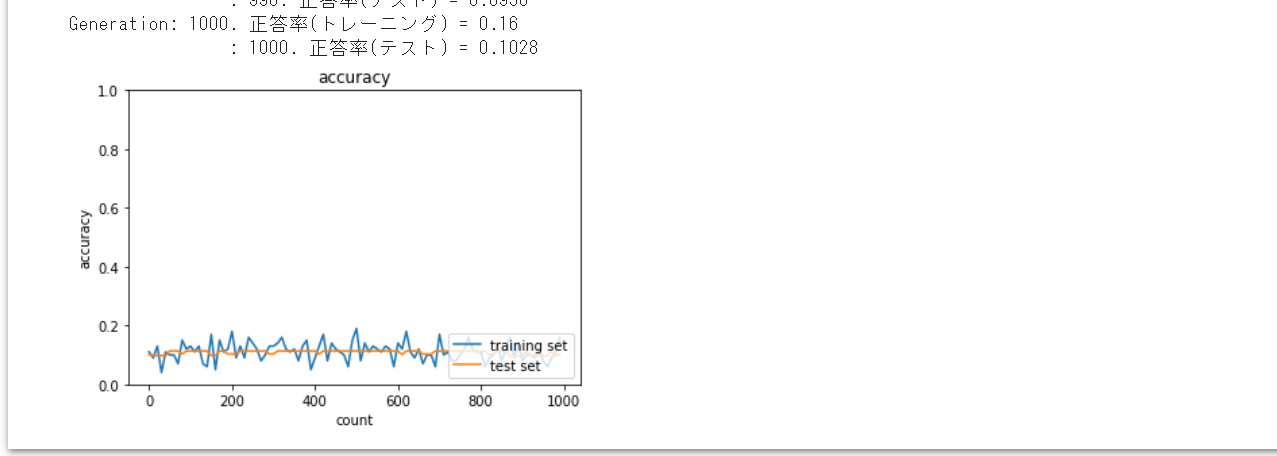
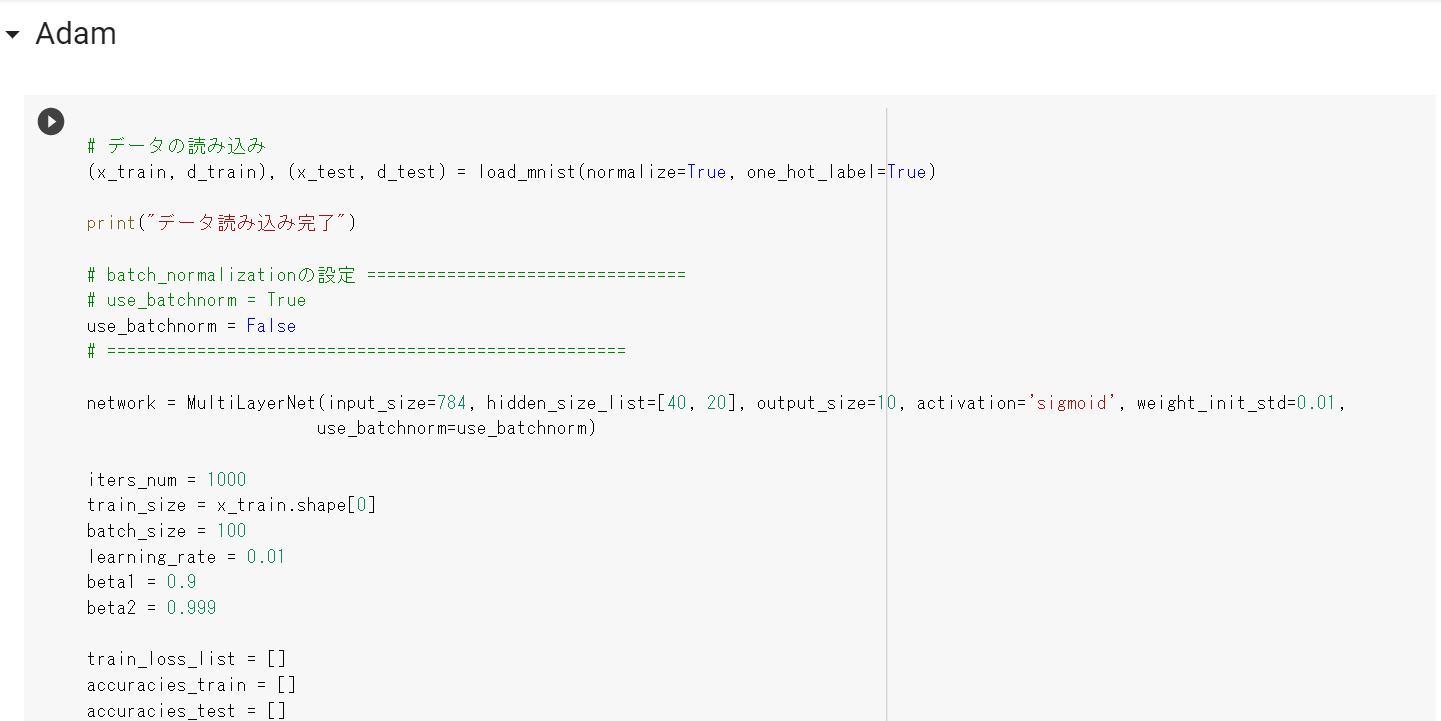
■演習
SGDでは、勾配消失問題が発生し学習が進まないことが確認された。
今回、学習率最適化手法 (モメンタム、AdaGrad、RMSProp、Adam) を使用して
勾配消失問題を回避できるか確認してみた。
結果として本モデルでは、モメンタム、AdaGradでは勾配消失問題が
発生し学習がうまく進んでいかなかったが、RMSProp、Adamでは
勾配消失問題を回避し学習はうまく進んでいくことが確認された。
##Section3：過学習について
■過学習
テスト誤差と訓練誤差とで学習曲線が乖離すること
■正則化
ネットワークの自由度 (層数、ノード数、パラメータの値等) を制約すること
⇒正則化手法を利用して過学習を抑制する
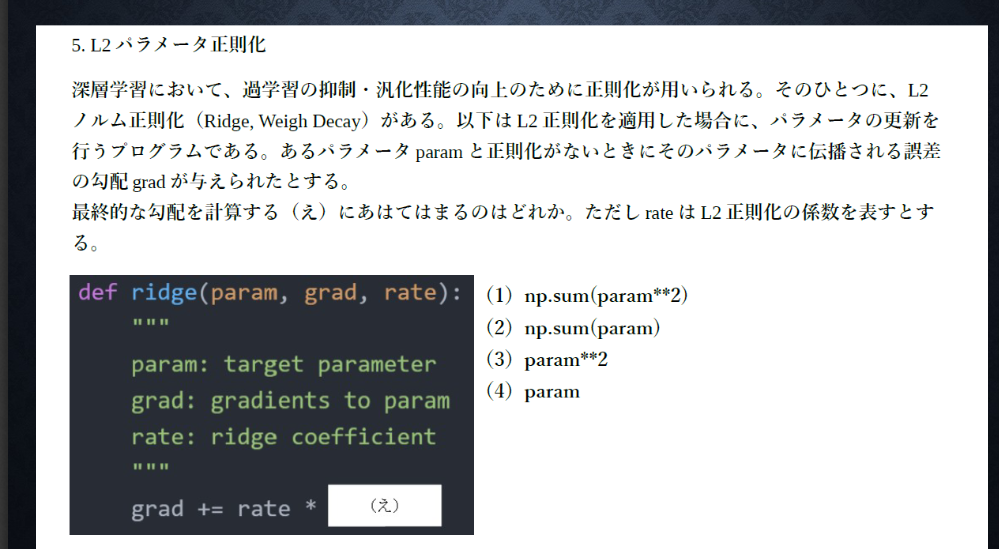
■L1、L2正則化
$$E_n(\boldsymbol w)+\frac{1}{p}||x||_p$$
$$||x||_p=(|x_1|^p+\cdots+|x_n|^p)^ \frac{1}{p}$$
$p=1$の場合，L1正則化と呼ぶ．
$p=2$の場合，L2正則化と呼ぶ．
■確認テスト
下図についてL1正則化を表しているグラフはどちらか答えよ。
・解答
右側 (Lasso推定量) のグラフ
■例題チャレンジ
・解答
(4)
■例題チャレンジ
・解答
(3)
##畳み込みニューラルネットワークについて
■畳み込み層
画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し
次に伝えることができる。
結論として3次元の空間情報も学習できるような層が畳み込み層である。
■パディング
畳み込み層の処理を行う前に、入力データの周囲に固定のデータ (例えば0など) を
埋めること。
■ストライド
フィルターを適用する位置の間隔のこと。
■確認テスト
サイズ6×6の入力画像をサイズ2×2のフィルタで畳込んだ時の
出力画像のサイズを答えよ。
なおストライドとパディングは1とする。
・解答
7×7