領域四分木で当たり判定を高速化する 理論編

対象読者

ゲーム開発をしていて当たり判定を高速でしたい人 or データ構造に興味がある人

はじめに

本テーマは既にいくつかの文献で説明がされています。しかし、今広まっている実装よりも洗練された実装があります。また、理論的な側面をちゃんと説明した文章が見つからなかったため今回筆を執った次第です。途中難しいと感じる部分があるかもしれませんが、実装には関係ないところもあるので適宜飛ばして読んでください。

どういうデータ構造？

「当たり判定の回数」を「簡単な事前計算」を元に大きく減らす枝狩り手法です。特に、事前計算が非常に早いことが特徴になります。

あるオブジェクトと衝突しうるのは、そこに近いオブジェクトだけ。遠いオブジェクトとはそもそも当たり判定を計算する必要がありません。そこで領域を四角形で分割し、オブジェクトを内包する軸並行矩形 (これは高速に計算できると仮定します) を元にオブジェクトを適切な領域に割り当てます。
そして本当に当たり判定をしなければいけない領域にあるオブジェクトとだけ当たり判定を行います。
これによって、当たり判定そのものの回数を劇的に減らすことができます。

これはオブジェクトを内包する軸並行矩形の図です。外接している必要はないですが、外接しているとより良いです。
矩形は斜めには取れないことに注意してください。例えば楕円は外接矩形を簡単に計算できますが、軸並行にならないのでダメです。 (以下、ダメな例)

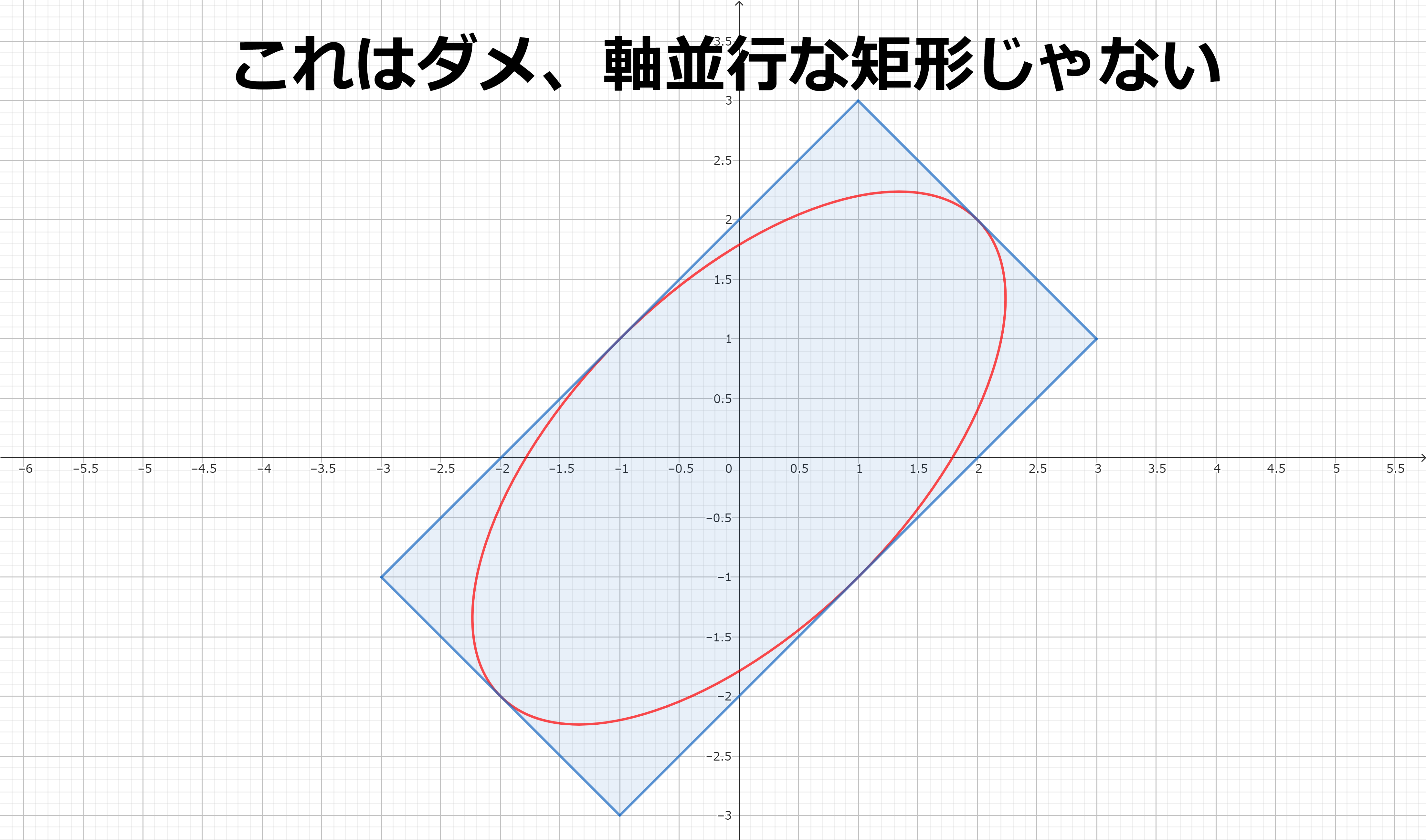
このデータ構造の上手い部分は、オブジェクトを内包する軸並行矩形→領域 への計算を爆速でできるようにしている部分です。後ほど説明します。

適応できる問題

円や軸並行矩形 などの2次元の当たり判定をもつ 移動しうる 物体が大量にあり、多対多 の当たり判定の回数を減らして高速化したい場合。

複雑な図形は複数の円や軸並行矩形の和集合で近似すれば問題ありません。

今回は2次元での当たり判定を扱いますが、実はこの記事で述べた方法は一般に任意の次元 $d$ に拡張できます
その場合、$2^d$ 分木を使います

以下補足

なぜ円や軸並行矩形かというと、外接軸並行矩形が高速に計算できるからです。楕円などは外接軸並行矩形の計算が面倒です。とはいえ内包する軸並行矩形の計算は高速にできるのですが、楕円が細長く傾いている場合はスカスカになるので結局この手法による恩恵は少ない気がします。楕円の大きさが小さいときはありかもしれません。(要考察) 凸包は回転しないのなら軸並行矩形は事前に1度計算すればその後O(1)で計算できるのでかなりありだと思います。

また、一対多なら愚直な当たり判定を計算するので十分な場合が多いですが、1回の当たり判定の計算が重い場合はこの手法によって当たり判定そのものの回数を減らすことができるのでその場合も有用です。

領域四分木の理論

理論編なので公理的な考え方で説明してきます。
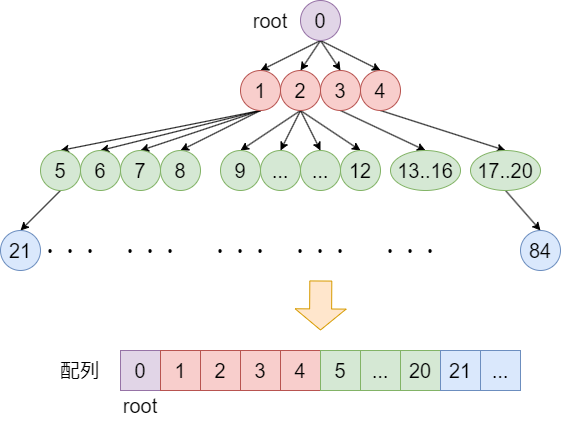
木を考えます。あるノードは子を4つもつか、あるいは葉です。これからノードと領域を対応させます。

1. 親の領域は4つの子の領域の非交差和とし、根には空間全体を対応させます

   {Area}_{parent} = \bigsqcup_{child} {Area}_{child} \tag{1}
   

2. 木は完全4分木にします
3. 領域を2のべき乗の正方形で分割し、各深さごとに、z階数で順序づけて木のノードと対応させます

オブジェクトは、それが完全に含まれる中で最小の領域をもつノード1つに登録されます。言い方を変えると、ノードはオブジェクトのリストを持ち、同じオブジェクトを持つ異なるノードはないとします。

性質1から導かれる当たり判定の枝狩り

性質1：”親の領域は4つの子の領域の非交差和とし、根には空間全体を対応させる” から、
ノードAはノードBの子孫⇔ノードAのオブジェクトとノードBのオブジェクトは衝突する可能性がある⇔AとBの当たり判定をする必要がある
ことがわかります。これを使って木を根からの一回の巡回ですべての可能性のある当たり判定を計算することができます。具体的には、オブジェクトを入れるスタックを用意して、DFSでノードを訪問する際にノードに登録されているオブジェクト達の間でまず当たり判定を行います。次に、ノードに登録されているオブジェクト達とスタックの中のオブジェクト達で当たり判定を行います。そして、ノードに登録されているオブジェクトを全てスタックにpushして、子をDFSで辿っていきます。ノードからの帰りがけに、スタックからオブジェクトをpopしていきます。
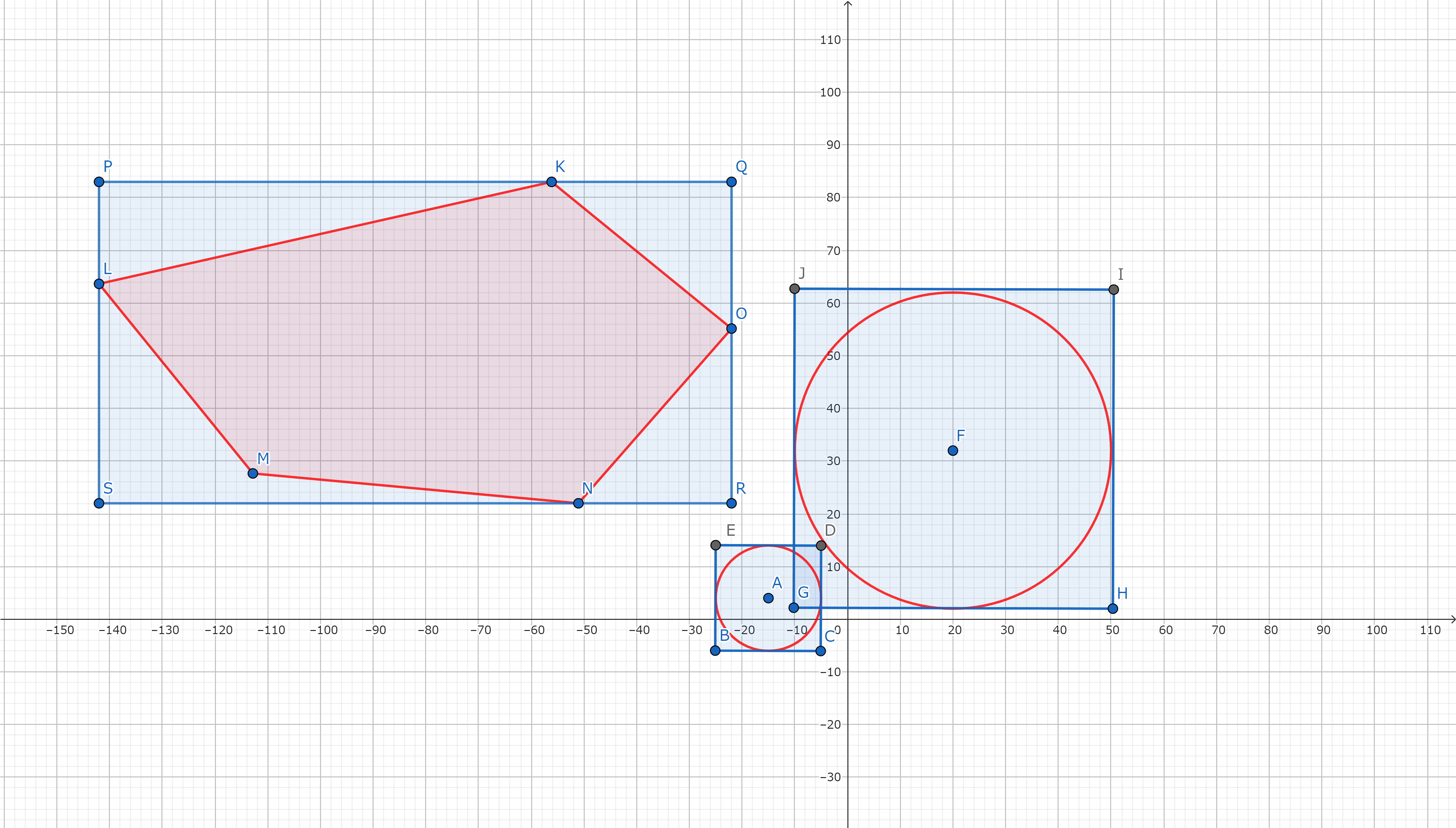
例を用いて説明します。

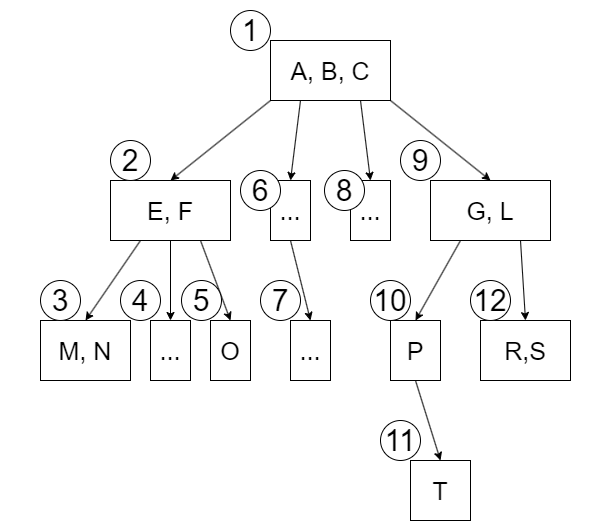
根からDFSをしていきます。図のノードに振られている番号はDFSによる訪問順 (行きがけ順) です。注意してください。

以下具体例の解説

1. スタック= [ ], ノード= [A, B, C] ノード内のA,B,Cで衝突判定を行います。その後 A, B, Cをスタックにpushして子を探索します。 2. スタック= [A, B, C], ノード= [E, F] EはF,A,B,Cと、FはE,A,B,Cと衝突判定を行います 3. スタック= [A, B, C, E, F], ノード= [M, N] MはN,A,B,...,Fと、NはM,A,B,...Fと衝突判定を行います。子がないのでM, Nをスタックにpushすることなく親に戻ります。 4. スタック= [A, B, C, E, F], ノード= [ ] 衝突判定は行いません 5. スタック= [A, B, C, E, F], ノード= [O] OはA,B,...,Fと衝突判定を行います。子がないのでOをスタックにpushすることなく親へ戻ります。さらに、親の[E,F]は全ての子を探索し終えたので、[E, F]をstackからpopして戻ります。 6. スタック= [A, B, C], ノード = [ ]

(中略)
10. スタック= [A, B, C, G, L], ノード= [P]
PとA, B, ..., Lで衝突判定を行います。
12. スタック= [A, B, C, G, L], ノード= [R, S]
RはS, A, ..., Lと、SはR, ..., Lと衝突判定を行います。

長々と書きましたが、[A, ..., T] の全ての組で衝突判定するより、当たり判定そのものの回数をかなり減らせているということです。

性質2による実装の定数倍高速化

性質2：”木は完全4分木にする” によって、一般の四分木と違い動的に分割しないので木をポインタで実装する必要がなく、木を 配列で実装できる のでアクセスが高速化します。特定のノードへのアクセスは根から辿らず直接アクセスでき高速ですし、親や子へのアクセスもポインタを辿らないので高速化できます。後者は二分ヒープの完全二分木による実装と全く同じ話です。

以下の図のように、親のノード番号が $i$ なら、子のノード番号は $4i+1, 4i+2, 4i+3, 4i+4$ です。
逆に 子の番号が $i$ なら、親のノード番号は $\left\lfloor \frac{i-1}{4} \right\rfloor$ になります。

性質3 (z値) による 座標→領域 の爆速計算

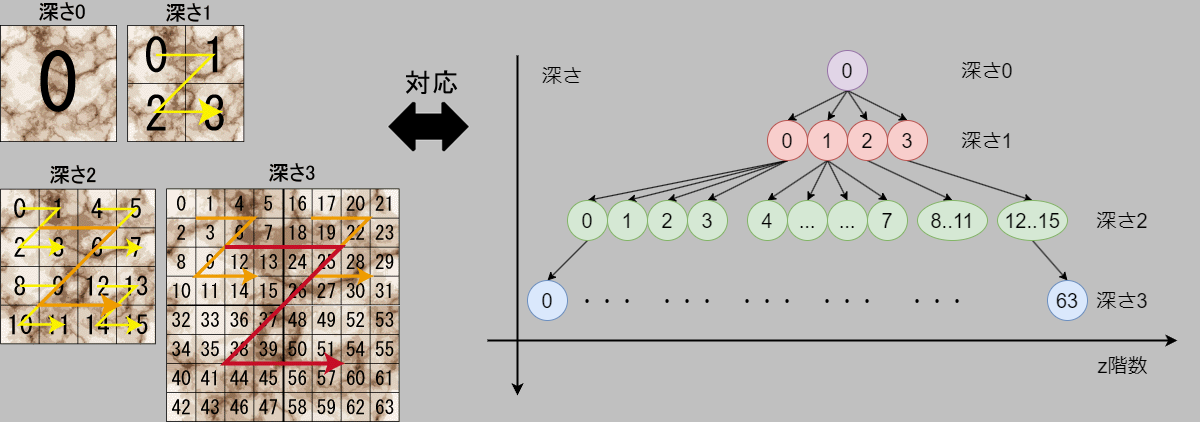
性質3の”領域を2のべき乗の正方形で分割し、各深さごとにz階数で順序づけて木のノードと対応させる” とは以下の図のようなことです。

「ノード番号」は木を通してのノードの通し番号、「深さ $d$ のz値」は深さ $d$ のノードの中でのz階数を表します。
混同に気を付けてください。上の図の番号は、「深さ $d$ のz値」の説明です。以降もこの2つの用語は厳密に使い分けます。

これからの目標：オブジェクトがすっぽり入る空間を求める=深さと、その深さでのz値を求める

このz階数のもつ性質について、具体的な例を用いて説明します。以下では深さ3、つまり$2^3=8$ 分割している状況を仮定して説明します。

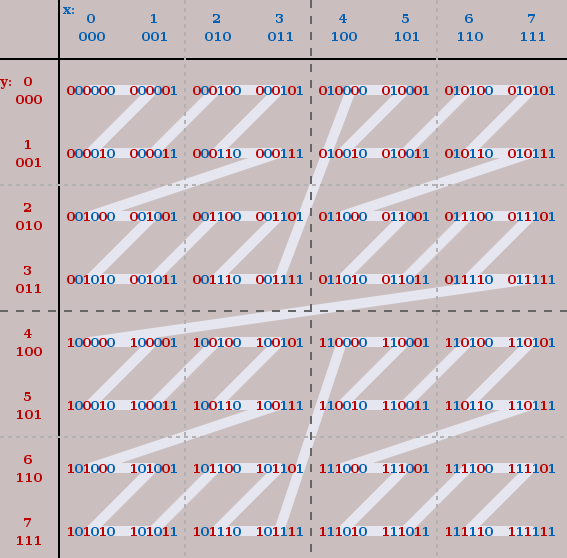
グリッド座標から、最も深い空間でのz値の計算

8分割なので、x座標は0から7の値を取ります。z値を2進数で表した上の表を見ると、x座標の値はz値の偶数番目のビットを抜き出したものに現れています！同様に、y座標の値はz値の奇数番目のビットに現れています。表を上から下、左から右に見てみるとわかります。
よって、点のx座標とy座標が分かればビットをずらして重ねることで、簡単に最大深さのz値を計算することができました。これは計算機で簡単なビット演算で実現できます。

任意の深さでのz値の計算

ここがz値である理由の全てです。z値はそれより浅い深さのz値の情報を保持しています。深さ $d$ でのz値から、深さ $d-1$ のz値は、深さ $d$ のz値を4で割って切り捨てた値になります。よって、深さ $d-k$ のz値は $\lfloor {z_d}/{4^k} \rfloor$ で計算できます。これは計算機で $2k$ ビットシフトするだけです。

補足ですが、x座標, y座標を1bit削る(2で割る) った後に、xとyのビットをずらして重ねた結果、前のz値から2bit削った(4で割った)値になったと解釈できます。

四角形のすっぽり入る空間の深さを求める

四角形の対角の2点が $(x_1, y_1), (x_2, y_2)$ と与えられているとします。
このとき、$(x_1\oplus x_2)\parallel (y_1\oplus y_2)$ のMSB (Most Significant Bit) を見ることで四角形がすっぽり入る領域の深さがわかります。ここで、$\oplus$ はbitごとの排他的論理和(xor)のことで、$\parallel$ はbitごとの論理和(or)です。
これは、次元ごとに考えれば理解できます。以下の図を見てください。

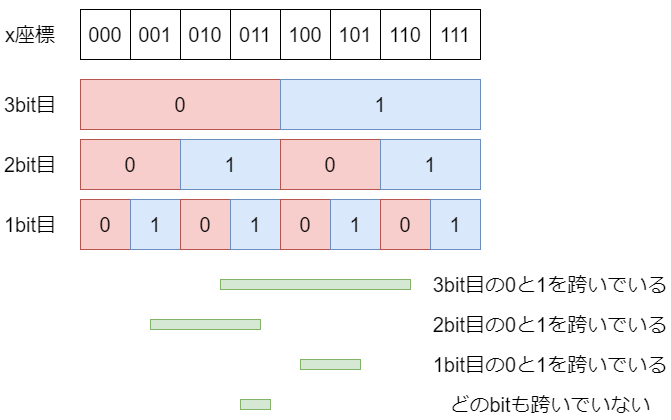
図より、$x_1とx_2$がbitの境界線を跨いでいるかは、$x_1\oplus x_2$ が1になっている最も左側のbitを見れば、線分がすっぽり入る領域の細かさがわかります。
2次元になった場合、領域は縦横同じ幅をもつので、xとyそれぞれのxorのMSBのうち、大きいほうを採用すればいいわけです。これは、$(x_1\oplus x_2)\parallel (y_1\oplus y_2)$ のMSBを見るのと同じです。

まとめ：四角形のすっぽり入る空間の深さとz値を求める

四角形の対角の2点が $(x_1, y_1), (x_2, y_2)$ と与えられているとします。

1. どちらか片方の $(x, y)$ を使って、グリッド座標から、最も深い空間でのz値の計算 の方法で点の最も深い空間でのz値を計算します
2. 四角形のすっぽり入る空間の深さを求める の方法で、すっぽり入る領域の深さを計算します
3. 任意の深さでのz値の計算 の方法で、最も深い領域のz値からその深さでのz値を計算できました

全部合わせてO(1)ですね。しかも3つ全てが単純なbit演算で実現できることは驚くべきことです。つまり、定数倍でもかなり速いことが期待されます。

理論編まとめ

領域を2のべき乗の正方形で分割し、各深さごとに、z階数で順序づけて完全四分木のノードと対応させました。
すると、オブジェクトを内包する軸並行矩形→オブジェクトがすっぽり入る領域をO(1)で計算できました。
木をDFSで巡るだけで、必要最低限の衝突判定の回数で計算できます。

以上。

つづき

参考文献

• 4分木空間分割を最適化する！（理屈編）
  http://marupeke296.com/COL_2D_No8_QuadTree.html
• wikipedia Z階数曲線
  https://ja.wikipedia.org/wiki/Z%E9%9A%8E%E6%95%B0%E6%9B%B2%E7%B7%9A