ボウリングデータで階層ベイズ

この記事は Stan Advent Calendar 2016 の6日目の記事です。

こんにちは。
そろそろ年末ですね。
忘年会のお話がちらほら聞こえてくる頃でしょうか。
そんな折，Stanをこよなく愛する紳士に「なんでもいいから今すぐMCMC(*´Д`)ﾊｧﾊｧするのだ」という指令を頂きましたので，初ブログを書いてみようと思います。
基本的にアヒル本を参考にしながらやっています。
アヒル本すごく楽しく読ませて頂いています。

アヒル本はこちら
StanとRでベイズ統計モデリング(Wonderful R)

今回は，昨年の忘年会のボウリングデータを使って階層ベイズをやってみたいと思います。
ですが，私はまだベイズもStanもRも初心者ですので，勘違いしているところがたくさんあると思います。訂正のコメントを頂けたら有難いです。
あと，私自身は心理学を専攻していますので，最後にほんの少しだけ心理学や教育学の研究における階層モデルの応用について述べたいと思います。
環境はR3.2.2，Rtools3.3，Rstan2.12.1です。
よろしくお願いします。

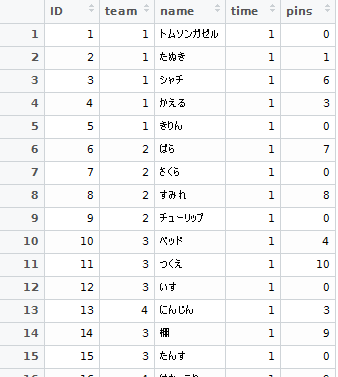
今回使うデータセットは，以下のようになっています。

個人を識別するIDとチームを識別するID，1フレームで何本ピンを倒したかが入っています。
人数は29名で，チーム数は6です。2ゲームしてるので，一人につき20フレーム分のデータがあります。

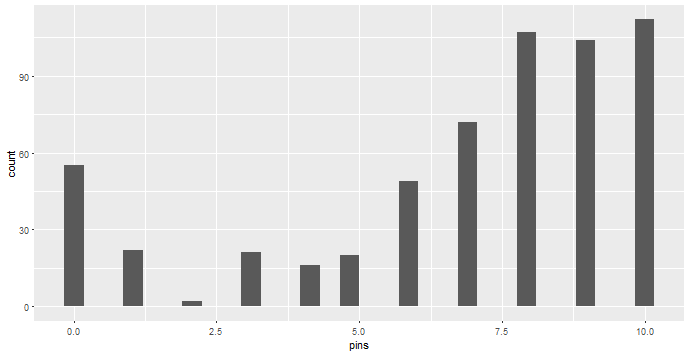
ヒストグラムを描くとこんな感じです。

このボウリングの倒れたピンのデータが試行数10の二項分布に従うものと仮定して分析していきたいと思います。

個人差・チーム差を考慮しないモデル

まずは，個人差もチーム差も考えないで，すべてのデータが同じ二項分布から生成されたと仮定して推定したいと思います。
Stanコードはこんな感じです。

b1.stan

data{
  int<lower=0> N;  //データ数
  int<lower=0> Trial[N];  //試行数
  int<lower=0> Y[N];  //データ
}

parameters{
  real<lower=0,upper=1> pi; //推定する成功確率
}

model{
  for(n in 1:N){
    Y[n] ~ binomial(Trial[n],pi);  //尤度関数
  }
  pi ~ uniform(0,1);  //事前分布
}

これを実行するRコードは以下のようになっています。

b1.R

b1 <- stan_model("b1.stan")      # Stanコードのコンパイル
Trial <- rep(10,nrow(b))             # 試行数データの作成
bdat <- list(N=nrow(b),Trial=Trial,Y=b$pins)  # Stanに読み込むデータの作成
b.fit1 <- sampling(b1,bdat)      # サンプリング
print(b.fit1,digits=3)       # 結果の表示, digitsは表示する小数点以下の指定。

modelのところには，今回得られたボウリングデータY[n]が試行数T[n]（今回は10），成功確率piの二項分布から生成されていると仮定したことと，成功確率piに無情報事前分布として範囲[0,1]の一様分布を仮定したことが表現されています。

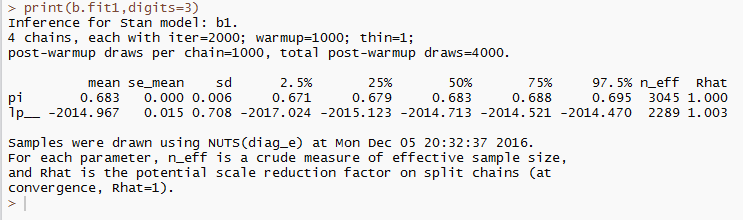
結果はこんな感じです。Rhatが1.01以下であり，有効標本数も十分なので，収束していると考えられます。トレースプロットや自己相関，密度関数なども問題なかったので，今回は省略します。

個人差もチーム差も考えずに，すべて同じ二項分布から生成されたと仮定した場合，サンプリングによって近似された二項分布の成功確率の事後分布は，事後平均が0.68であり，事後標準偏差が0.01だということがわかりました。つまり，平均的には1フレームで（10本中）だいたい6.8本くらいピンは倒れるということがわかりました。

チーム差を考慮したモデル

つぎに，チームで共通した部分とチームによって異なる部分とを分けて考えて，推定したいと思います。

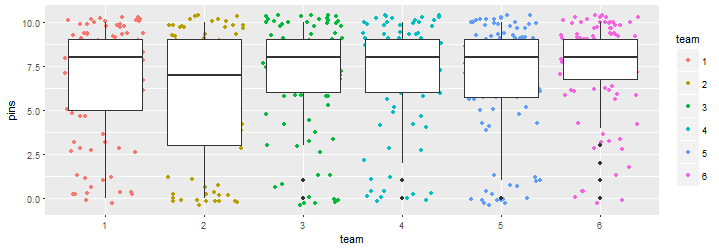
まず，横軸にチームを，縦軸に倒れたピンの数をとって，散布図とボックスプロットを描いてみます。

あまりチームによる差はなさそうですね。なかなかいい勝負だったようです。

チームによらず共通している成功確率と，チームごとの成功確率を分けて推定するためのStanコードはこんな感じです。

b2_1.stan

data{
  int<lower=0> N; //データ数
  int<lower=0> M; //チーム数
  int<lower=0,upper=M> team[N]; //チームID
  int<lower=0> Trial[N]; //試行数
  int<lower=0> Y[N]; 
}

parameters{
  vector<lower=0,upper=1>[M] pi; //チームごとの成功確率
  real<lower=0,upper=1> mu;  //チームによらず共通する成功確率
  real<lower=0> sigma;  //チームごとの成功確率のばらつき
}

model{
  //尤度関数
  for(m in 1:M){
    //チームごとの成功確率が，Normal(mu,sigma)から生成されている
    pi[m] ~ normal(mu,sigma);  
  }
  for(n in 1:N){
    //データYがチームごとの成功確率を持つ二項分布から生成されている
    Y[n] ~ binomial(Trial[n],pi[team[n]]);  
  }
  //事前分布
  pi ~ uniform(0,1);
  mu ~ uniform(0,1);
  sigma ~ student_t(4,0,10);
}

今回は，チームごとの成功確率（pi。piはチーム数分あります。今回は6つ）とチームによらず共通している成功確率（mu），チームごとの成功確率のばらつき（sigma）を推定していることが表現されています。ここでは，チームごとの成功確率が，範囲[0,1]の平均muと，標準偏差sigmaの正規分布から生成されていることを仮定しました。事前分布について，チームごとの成功確率とチームによらず共通している成功確率には，無情報事前分布として範囲[0,1]の一様分布を，チームごとの成功確率のばらつきには，「範囲[0,1]の確率のばらつきは，0から大きく離れることはない」という情報をもとに，弱情報事前分布として自由度4，平均0，標準偏差10の半t分布を仮定しました。

チーム差を考慮しないモデルでは省略しましたが，自分の書いたStanコードが正しく推定するのかどうかをRでシミュレーションによって確認することは重要ですよね。
そのためのRコードは以下のような感じです。

b2_1test.R

# チームによらない成功確率
mu <- .5
# 成功確率のプロビット変換
q_mu <- qnorm(mu)
q_mu
# チームごとの成功確率のばらつき
sigma <- .8

# チームごとの成功確率の作成
set.seed(1234)
# まずプロビット値を乱数で発生させる
phi_rate <- rnorm(6,q_mu,sigma)
phi_rate
# プロビット値を正規分布の累積分布関数によって確率に変換する
theta <- pnorm(phi_rate)
theta

# 試行数10，チームごとの成功確率piの二項分布からデータを生成
Y <- rbinom(600,10,theta)

# チームのID
Team <- rep(1:6,100)

# 試行数データの作成
Trial <- rep(10,600)

# Stanに読み込ませるデータの作成
dt2 <- list(N=length(Y),M=6,Trial=Trial,team=Team,Y=Y)

# サンプリング
b.fit2t <- sampling(b2_1,dt2)

# 結果の表示
print(b.fit2t,digits=3)

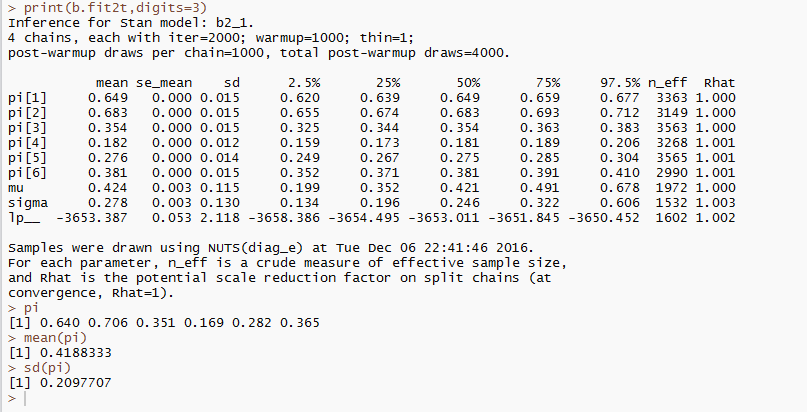
結果はこんな感じです。

おおむね推定はうまくいっているようです。
実際は，何度かパラメータの設定を変更して，うまく推定できるか確認することが必要ですが，今回は省略します。

それでは，実データにあたってみたいと思います。
実行するRコードは以下のような感じです。

b2_1.R

b2_1 <- stan_model("b2_1.stan")
Trial <- rep(10,nrow(b))
bdat2 <- list(N=nrow(b),M=6,Trial=Trial,team=b$team,Y=b$pins)
b.fit2 <- sampling(b2_1,bdat2)
print(b.fit2,digits=3)

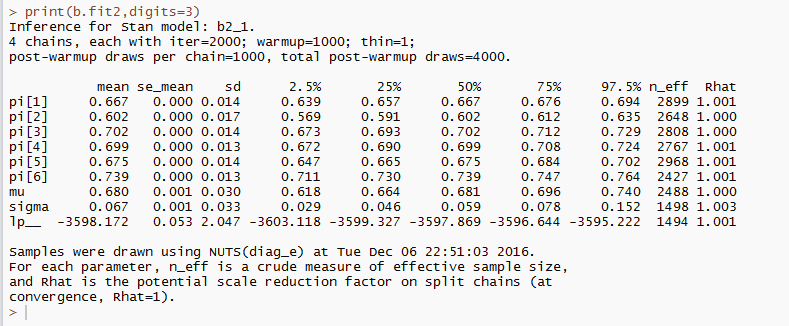
結果は，以下のような感じです。Rhatがすべての母数に関して1.01以下であり，有効標本数も十分であるため，十分収束していると判断しました。トレースプロットや自己相関，密度関数を確認することは重要ですが，問題なかったので，今回は省略します。

推定結果から，チームによらず共通している成功確率は事後平均で0.68であり，チームごとの成功確率はチーム6が事後平均で0.739と最もピンを倒す確率が高いことがわかりました。また，チームごとの成功確率のばらつき（sigma）は事後平均で0.067，事後中央値で0.059とあまり大きくはないことがわかりました。本来は，generated quantitiesブロックで，推定した母数を使って色々分析できると思いますが，そこはまたつぎの機会にしたいと思います。

心理学や教育学などの研究で

心理学や教育学などの研究場面では，今回のボウリングのチームを「異なる特徴を持つグループ」と捉えなおしてみるのもよいかと思います。たとえば，異なる6つのクラスで10点満点のテストを実施したといった例が考えられるかと思います。あるいは，階層のある回帰モデルも考えられると思います。つまり，ある変数xによる他の変数yへの影響が「異なる特徴を持つグループ」ごとで異なるというようなモデルです。たとえば，宿題の量が子どもの成績に与える影響は子どもの持つ特質によって異なることなどが考えられます。
また，ボウリングデータのチームを「実験に参加した個人」と捉え，チームにネストされている倒れたピンのデータを「実験参加者個人にネストされているデータ」だと捉えたら，この階層モデルは個人差による部分と個人差によらない部分を分けて見ていることになるかと思います。そのため，個人差を見たくない実験や逆に個人差によるばらつきに関心がある研究にも応用できると思います。
このほかにも推定した個人差やグループ差によるばらつきを他の変数によって説明するモデルや複数の階層を仮定するモデルなど階層モデルの応用範囲は広いと思います。

おそらくボウリングってチーム差よりも個人差の方が大きいのかなと思うので，本当はチーム差に個人差も加えた複数の階層を持つモデルもやりたかったのですが，今回は時間も技術も足りなかったので，またつぎの機会にやってみたいと思います。

読んでくださりありがとうございました。
それでは。

Enjoy, Stan!!