宇宙の彼方の重力レンズ
この写真は南半球のろ座に位置する GAL-CLUS-022058 。見事なアインシュタインリングが観察できます。

この画像の中央に見えるのは銀河団です。その銀河団の重力により、背後にある別の銀河団の像が拡大かつ歪んでリングのように見えています。
ここではレンズの重力源の銀河団が明瞭に見えますが、重力源がブラックホールの場合は中心に黒い穴がある形で見える場合があります。
CGによるブラックホールシュミレーション
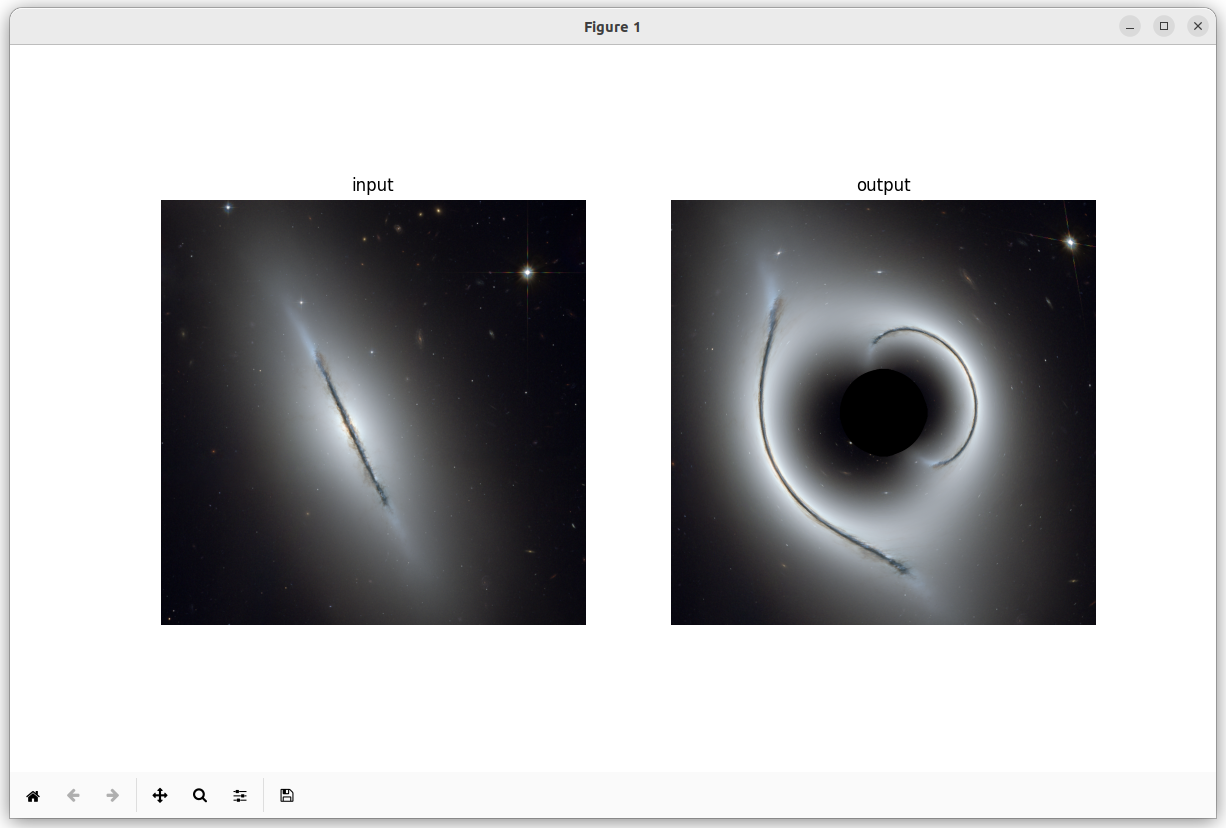
下はブラックホールの場合を想定したCGです。重力レンズ効果がない場合の通常の Ngc5866 銀河 の写真が左側。右側は銀河の手前にブラックホールがあった場合のシュミレーション。黒い穴が出現しています。
このシュミレーターは Python プログラムとして公開されています。
これを今回、試してみました。
環境
- Ubuntu Linux 22.04 LTS
- Python 3.10.12
ダウンロード、設定
上記のレポジトリからクローンします。
$ git clone https://github.com/Shaun-F/Gravitational-Lensing-Visualization.git
$ cd Gravitational-Lensing-Visualization/
動かすためには以下のモジュールが必要でした。
$ sudo pip install matplotlib
$ sudo pip install astropy
プログラム
$ tree
.
├── Grav_Lensing.py
├── Grav_Lensing_Image.py
├── Gravitational_Lensing_Image.ipynb
├── README.md
└── test_images
├── Ngc5866_hst_big.png
├── eso1738b.jpg
├── eso1738c.jpg
└── eso1738e.jpg
レンズ効果形状の計算
Grav_Lensing の方を動かしてみます。
$ python3 Grav_Lensing.py
太陽の 10^11 倍の質量の重力源が作り出す重力レンズが表示されます。
source は 重力源、lensed source は背景にある光源で、Einstein Ring の中心に存在します。

source を中心近くに持ってくるとアインシュタインリングが出現します。
うーん? 距離のパラメーターとかどうなっているのかな?
ソースに以下のように書かれてました。
D_S = 5000 #parsecs
D_L = 2000 #parsecs
D_LS = np.abs(D_S-D_L) #parsecs. distance from source to hole
G = c.G.value #gravitational constant
M = 10**11 #solar masses. Mass of lensing hole
5000パーセクと2000パーセクとなってますね。ちょうどM12球状星団(約16000光年)と、かに星雲(約6500光年)ぐらいの距離になります。
画像に重力レンズ効果を施す
$ python3 Grav_Lensing_Image.py
とすると、
ソースを見ると、画像ファイルはコードに埋め込まれていますね。
#Open the image file as a matrix of rgb values
# image_file = "./test_images/eso1738e.jpg" #relative path to image file
image_file = "./test_images/Ngc5866_hst_big.png"
image_data_unshapped = img.imread(image_file) #import image file as a matrix. Each component of the NxM matrix is a length 3 array containing the RGB values of the pixel.
image_min_side_inxlength = np.min(image_data_unshapped.shape[:2]) #find the minimum length of the image matrix. I.E. for an NxM matrix, which is smaller the 'N' or the 'M'?
image_data = image_data_unshapped[:image_min_side_inxlength,:image_min_side_inxlength] #crop the matrix using the minimum side length so that it is square. I.E. if 'N' is smaller, then reshape to an NxN matrix.
source_data = np.empty(image_data.shape) #Create the target matrix that will be populated by the lensed pixels of the input matrix
#setup the physical system
D_L = 500*u.pc # Distance to black hole in parsecs
D_S = 3000*u.pc # Distance to source object in parsecs. This assumes the stars in the image are distributed planarly and they are much further away from the hole than they are from each other. This assumption makes the math much easier
D_LS = np.abs(D_S-D_L) #parsecs. distance from source to hole
G = c.G #gravitational constant
M = 10**11*u.Msun #solar masses. Mass of lensing hole
C = c.c.to(u.m/u.s) #m/s. speed of light
R_E = np.sqrt((4*G*M*D_LS)/((C**2)*D_L*D_S)).decompose().value*radtoarcsec #Einstein Radius in arcseconds
schwarz_radius = (((2*c.G*M/(c.c**2)))).to(u.pc) # schwarzschild radius in parsecs
距離パラメーターは今度は3000パーセクと500パーセク、質量は同じで計算しています。
3000パーセクは 10000光年、500パーセクは1600光年。
比較として、太陽系から銀河中心まで25000光年、地球に最も近いブラックホールであるガイアBH1が1600光年です。
さて、画像はソースコードを書き換えたら何でも指定できそうなので、秋葉原ロボット部同人誌「ロー」のキャラクターを指定してみました。