お宝論文
1975年に発表された、軌道エレベーターの古典的な論文を見つけた。
「The orbital tower: a spacecraft launcher using the Earth’s rotational energy」
出典：JEROME PEARSON(1975) p.785
著者ジェローム・ピアソンは現在も宇宙企業スターテック社を経営していて、その Webサイトで読める。
http://star-tech-inc.com/papers/tower/tower.pdf
軌道エレベータの材料問題
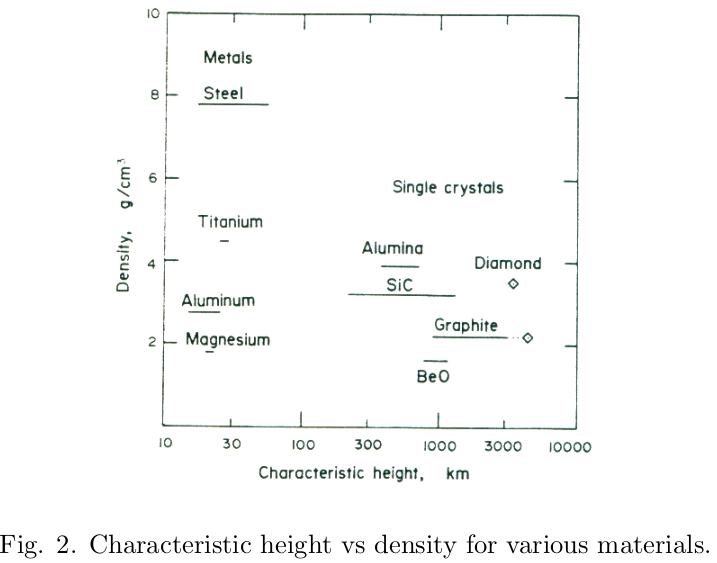
軌道エレベータの実現のための問題は十分な強度を持つ材料がこの世にないことである。現在の材料技術でも必要とされる強度に達しないが、当時の材料技術において単結晶グラファイトが検討されている。
出典：JEROME PEARSON(1975) p.789
このグラフの Characteristic height (特性高) は、現在一般に破断長と呼ばれているもの。
一定の断面積を持つ細い材料を、均一な重力加速度 9.8m/s で垂らしたときに自重で切れる長さが破断長。それが最低4960kmあれば、軌道エレベータが実現できるとされている。
「◇」マークは理論的強度で、単結晶グラファイトの理論強度はなんとか4950km を満たしていそうだけれども、論文では実験室での計測を元に h=2150km を元に議論をしている。
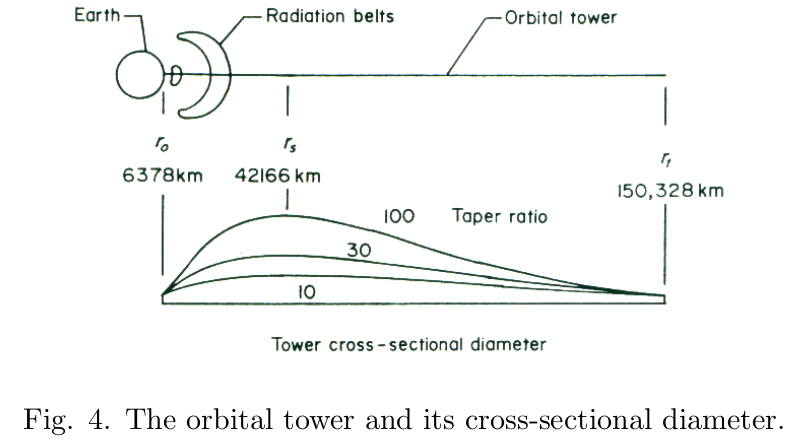
破断長 4960km を満たさずにどうすればいいか? 論文では軌道から垂らすエレベータケーブルであるテザーにテーパーをつける理論を展開している。
テザーの地表高度での断面積 $A_0$ よりも重心位置の断面積 $A_s$ を大きくすることで、小さな破断長の材料でも軌道エレベータを作ることが可能となる。
パラメータ h (破断長=特性高) とテーパー比 $A_s$/$A_0$ の関係は論文中の式10で示され、
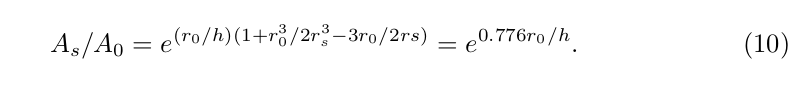
出典：JEROME PEARSON(1975) p.788
これを図で表すと
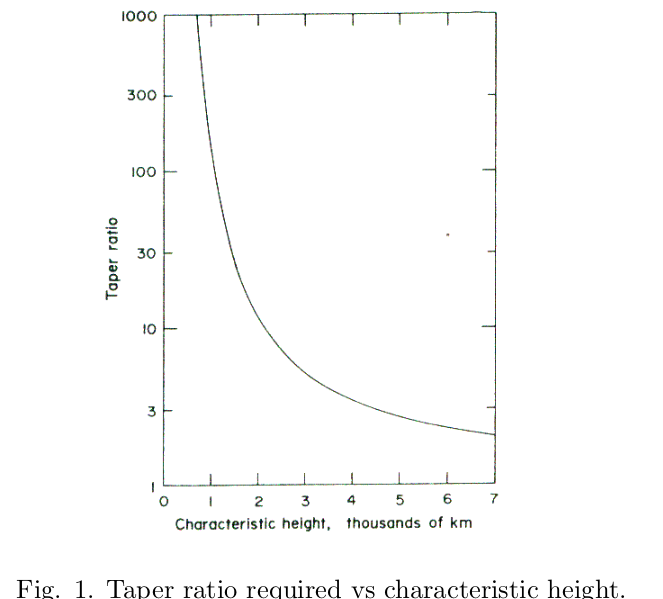
出典：JEROME PEARSON(1975) p.788
破断長2150kmだとテーパー比10程度が必要となることがわかる。
現在の材料
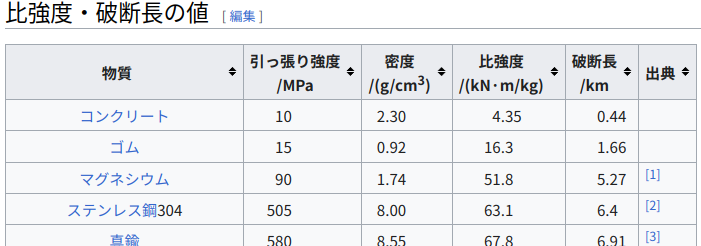
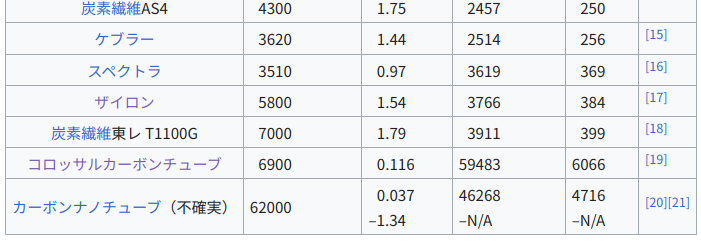
残念ながら破断長 2150km の単結晶グラファイトは論文発表後50年以上経過した現在でも、実用材料として実現となっていない。
において、
︙
とリストがあるが、
︙
破断長の十分大きな値のものとして、カーボンチューブが挙げられている。
軌道エレベータといえば今はもっぱらカーボンナノチューブに話題が行き着いてしまうけれども、しかしながらそれらはあくまでも未来の期待値であり、技術のブレークスルー待ちになっている。いつ解決するかは予定を立てられるものではない。
さて、それらを待たずに今ある技術、せめて少なくとも実現可能性の強いものでなんとか考えられないだろうか?
挙げられているものの中で実用材料としては「炭素繊維東レ T1100G」が最大のものとなっている。
これを元に、希望的な計算をしてみよう。
もうちょっとだけ背伸び
「東レT1100G」の破断長が 399 km であるけれども、2割強欲を出せば軌道エレベータに必要な最低破断長の1/10 である 496kmとなる。
この強度の追加分が表題のα。この値でなんとか軌道エレベータを実現できないだろうか?
テーパー比を計算
式(10) にあてはめて計算すると、テーパー比は 22000 となる。
なお、テーパーは直線錐というわけではなく、以下のように地球中心から42166kmの静止軌道で max となりより外側に長く伸びる曲線形状となる。
出典：JEROME PEARSON(1975) p.790
フルスペックで考えると・・・
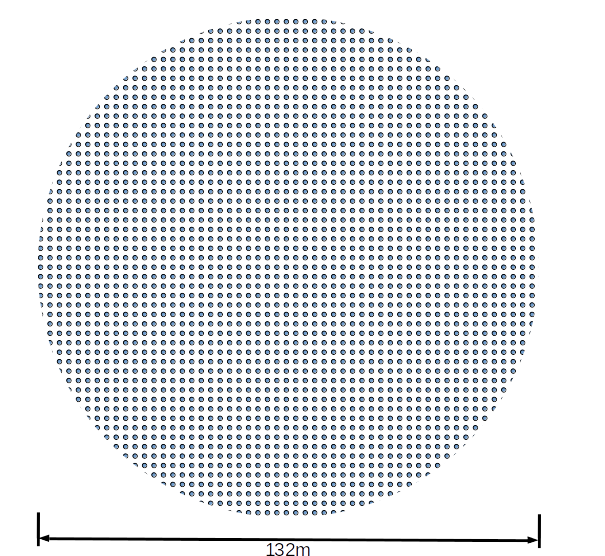
地表で 1 平方メートルの断面積を持つテザーとすれば、断面積の最大部は 22000 平方メートルとなることになる。
これはあまりにも大げさなので、地表で0.025平方メートル(円柱形にして直径20cm弱)のテザーを複々線として運用することを考えてみた。
これを静止軌道上で2200平方メートルになるとすると、断面積1平方メートルのテザー2200本を2.5mのグリッドで配置したとして、こんな感じかな。
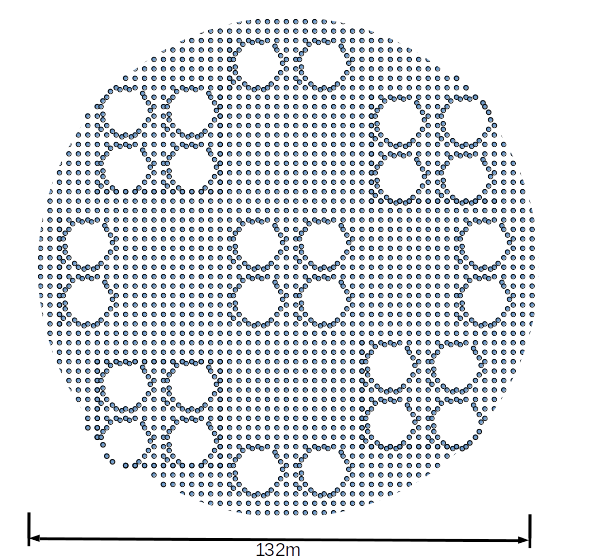
これだと使いでが良くないので、植物のように導管を作ってみたら・・・
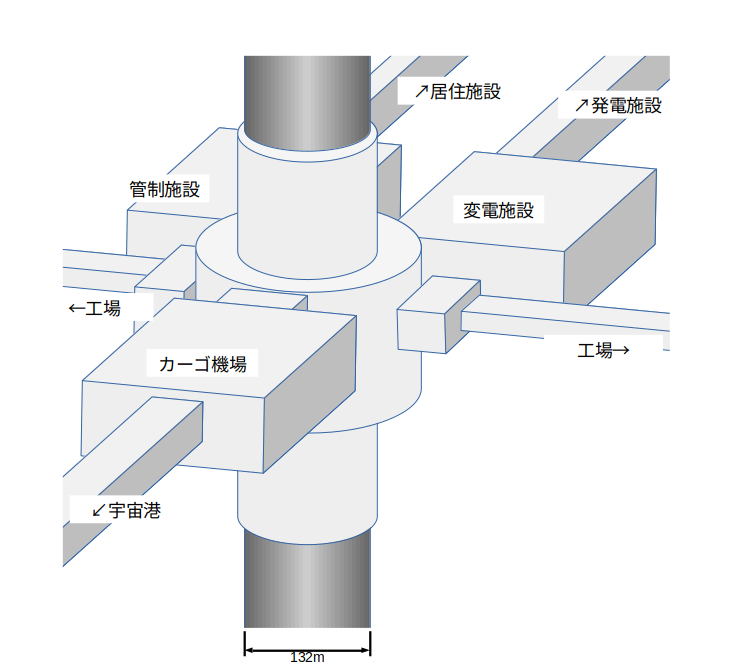
結構大掛かりになりますね。これらを維持するためには、静止軌道上にこのくらいの施設が必要じゃないかな?
こんな施設を除外して、テザーだけだとしてもかなりの分量になりそうです。
テザーの全体は、先に示した図では、静止軌道を超えて150328kmまで延びていました。
出典：JEROME PEARSON(1975) p.790
これだけの長さのテザーだと、仮にテーパーが無いとしても、
(150328km-6378km)10^3 0.1 1.7910^3 = 2.58万トン
テーパー比22000となると更にこれの10000倍以上もの材料が必要となり、 大体2〜3億トンとなります。
うーん、軌道エレベーターは安いコストで宇宙に行けるということなのですが、こんなのを静止軌道に作ったら予算がいくらあっても足りませんね。
考え直してみます。
1/1000 に縮小
先の想定は地表に0.025平方メートルの断面積のテザーを4本で降ろしました。テザーの引張強度は 8000 〜 9000 MPa/m^3 位を想定しているので1本のテザーで2万トンを持ち上げることができます。実際には安全比率や大気の擾乱、軌道のずれの吸収などでの力学があるためにこれから減りますが、そこらへんの考慮をもっと減らしてみましょう。
これを地表で10x10^-3 平方メートル すなわち断面積 1平方cm のテザー1本だけの構造で考えてみます。
これでも、80〜90トンを持ち上げることができます。静止軌道上では2.2平方メートルということになります。
だいぶ小さくなったかな・・・?
テザーの全体重量も 1/1000 となり、20万トン〜30万トンとなります。
うーん、宇宙に30万トンを輸送!?
ロケットで持っていくのはだいぶ問題がありますね。
ブートストラップ
吊橋の建設でエアスピニングという工法があります。吊橋のワイヤを一度にかけるのではなく、まず細いワイヤを1本だけ通し、それを伝って2本目、3本目のワイヤをかけて補強していく方法です。
同様に軌道エレベータも最低限のテザーを地表に降ろし、それを伝って地表から登っていきながら補強するという方法をとることができます。
仮に、最初のテザーが地表で1平方ミリメートルの断面積を持ち、800〜900kg を持ち上げることができるものとすると・・・静止軌道上の断面積は220平方cm、円柱にして直径16cm程度となります。
しょきテザーの全体重量は200トン〜300トン。
15億ドル
これを安いロケットで打ち上げるとして Falcon Heavy で10回分。打ち上げ費用は15億ドル。打ち上げ費用だけなので、材料費や地表から登っていくクライマーの費用、地表や軌道上の基地を作成する費用、などをこれにプラスしていくことになります。
さて、全体はいくらになるか・・・
俺達の戦いはこれからだ!