この記事はRust wgpuで3DCGに挑戦するの姉妹記事になります。姉妹記事のほうは Rust 2 Advent Calendar 2020 - Qiita の20日目記事にもなっています!
2つの記事は、Unityによるゲーム制作に嫌気がさした筆者が、ゲーム制作の未来を担うモダン言語Rustでゲーム制作を行うために3DCGをやってみるという内容です。本記事ではこのうち、理論編ということで、今回取り組むうえで必要だった知識について、Rustとwgpuに関係ない部分を簡単にまとめています。3DCGを行うためのすべての知識を列挙しているわけではない点に注意してください。
Unityで3Dモデルをロードする方法(あるいはBlenderで3Dモデルをエクスポートする方法)はいろいろありますが、その中でも扱いやすいObjファイルを使用して3Dモデルを描画できれば、Unityがなくても3Dゲームプログラミングが可能になるかもしれません!それが本記事の目標です!
本記事は、3DCGAPIとしてOpenGLやWebGL、Vulkan、WebGPUなどを想定し、GLSLに合わせた内容となります。検証はRustのgfxライブラリによる実装とRustのwgpuライブラリによる実装で行いました。とはいえ、GLSLはほとんど書かないつもりです。シェーダーファイルとの連携方法みたいな具体的な話は、フロントに使う言語(JavaScript & WebGLなのか、C++ & DirectXなのか、Rust & wgpuなのか...以降本記事のローカルルールとして便宜上 フロント側 などと呼ぶことにします。実際になんて呼ぶのかはわかりません。)によって大きく変わってしまうので、そういった話は今回はしません。Objファイルを描画するための基礎知識集という位置づけです。
0. リンク集
リンク集は通常最後に書くものだと思いますが、私の下手な記事よりも私が参考にしたサイトのほうが詳しいと思うので、最初のほうに載せさせていただきます()
- WebGLの基本
- 【3Dモデル】Objファイル基礎
- チュートリアル7:モデルのロード
- その70 完全ホワイトボックスなパースペクティブ射影変換行列
- Phongの反射モデル - Wikipedia
- その44 深度バッファシャドウの根っこ:0から原理を眺めてみよう
- Graphics by Squares: a Gfx-rs Tutorial
- Introduction | Learn Wgpu
WebGL Fundamentals (WebGLの基本) が基礎から書かれていて一番詳しいです。本記事で雰囲気をつかんで本格的に学びたくなった方に最適だと思われます。(JavaScriptのコードはかなり長くごちゃごちゃとしていますが...)
そのほか細かい情報については マルペケつくろーどっとコム さんの記事がめちゃくちゃ参考になります。ゲーム制作をする人はみなここにお世話になっているんじゃないかと思います。
前置きが長くなりました。早速内容に入りましょう!
1. 頂点シェーダー (Vertex Shader)
まずOpenGLやGLSLとはなんでしょうか?とても簡単に言えば「面倒な計算をGPUに任せるためのインターフェース」です1。
面倒な計算というのは、3DCGの場合「頂点の座標変換計算」と「ゲーム画面の1ピクセルごとの色の決定」になります。前者は頂点シェーダーで行い、後者はピクセルシェーダーで行います。
3Dモデル(ポリゴン)は時にはものすごい頂点数になります。そのため「頂点の座標変換計算」はものすごい計算量になります。面倒な計算と言ったのはそのためです。GPUはCPUに比べて簡単な並列計算がとても得意なので、こういった計算に向いているというわけです。
頂点シェーダ(Vertex Shader) で行う座標変換計算は、3DCGの場合二つの要素からなります。
単純な移動&3Dっぽくする
一つ目は、頂点を適切な位置に移動させるための計算です。
例えば1秒ごとにy軸中心で2°ずつ反時計回りに回転するポリゴンがあったとします。すべての頂点についてCPUで(例えば、普通のプログラミング言語で普通に)位置を計算するプログラムを書いたとすると、計算に日が暮れてしまいます。そこで、あらかじめ回転する量をシェーダにあげておき、回転する計算を並列に行わせます。
「3Dのように見せるための変換」を例にこの計算をビジュアル化してみたいと思います。
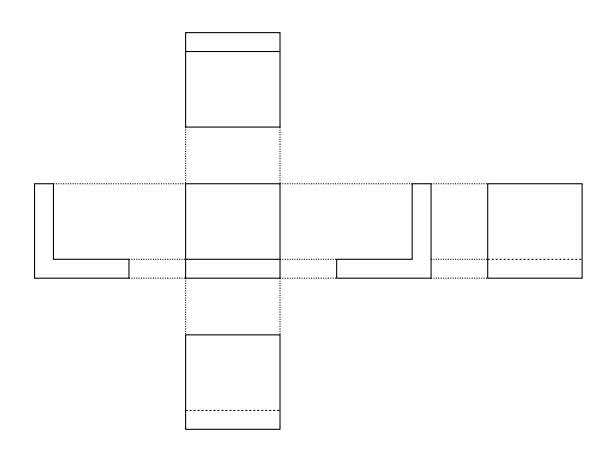
中学の技術科を思い出してください。三次元の物体を描く際、次のような「第三角法」で展開図のように物体を描くことがあったかと思います。
何も移動・回転計算を行わなかった場合、真ん中に描かれた正面から見た図形が表示されるでしょう。今度はこのL字物体を、同じく中学技術で扱ったであろうキャビネット図で描いてみると次のようになります。
キャビネット図は3D "もどき" な描画法ですが、人力でも簡単に描けるぐらい計算が単純です。
- もっとも前面にあたる正面図を普通に描く
- 奥の物体は、斜め45°の方向に、実際の距離の1/2で描く
よって、奥行きをz座標として考慮した場合2の作図に用いられる各頂点のx, y座標 (便宜上 $x'$, $y'$ としましょう) は次のように求まります。
\begin{eqnarray*}
x' &=& x + \frac{z}{2 \sqrt{2}} \\
y' &=& y + \frac{z}{2 \sqrt{2}}
\end{eqnarray*}
これをもとに座標変換するための行列を用いた式は以下のようになります。
\left[
\begin{array}{ccc}
1 & 0 & \frac{1}{2 \sqrt{2}} \\
0 & 1 & \frac{1}{2 \sqrt{2}} \\
0 & 0 & 1
\end{array}
\right] \left(
\begin{array}{c}
x \\
y \\
z
\end{array}
\right) = \left(
\begin{array}{c}
x' \\
y' \\
z'
\end{array}
\right)
頂点シェーダーでは、あらかじめこのような変換行列をシェーダーにアップロードし、そのあとに頂点をアップロードして計算を並列に行わせます。今例として挙げた変換行列が実際の3DCGで使われることはまずないと思います(やろうと思えば当然できます)が、原理的には同じようなことをしていると考えることができます。
具体的に考える計算は拡大・平行移動・回転になります。拡大行列、平行移動行列、回転行列は掛け合わせることができるので、シェーダーにアップロードする前に計算してしまいます。ただし、順番によって結果が変わる点に注意が必要です。
頂点シェーダーでの座標計算は WebGLの基本 の最初のほうでかなり丁寧に解説されています。行列の計算についても書かれており前提知識がなくても読みやすいのでおすすめです。
遠近法
頂点を移動させただけでは3次元のようにはなりません。近くの物体は大きく、遠くの物体は小さく描かれることで、より3Dに見せることができます。
遠近を決めるにはカメラが必要です。物体のワールド座標をカメラの座標に応じて変形させます。カメラには次に示すようなパラメータがあります。(すべてを頂点シェーダーで使用するとは限りません。)
- カメラ座標
- カメラの目線
- カメラの上方向 (目線軸の回転量)
- 画面のアスペクト(縦横)比
- 視野角
- near Z (描画する最も近くのZ座標)
- far Z (描画する最も遠くのZ座標)
これらの値から、視錐台というものを想定し、この台の中に存在する物体を描画するようにします。
遠近法に基づく変形について詳しい話は、次のサイトがとても参考になります。
私はRustでの実装ではパースペクティブ行列の用意をライブラリに頼りました。一から実装しても良いですが、車輪の再開発と思う3ならばそれぞれの環境において既存のライブラリの存在を調べると良いでしょう。
2. ピクセルシェーダー (Fragment Shader)
頂点シェーダーでは、ポリゴンの頂点位置を変形する処理を行いましたが、いわばテントの骨組みを組んだだけであり、テントに張った布については何もわかっていません。ピクセルシェーダー (Fragment Shader) ではこの頂点に囲まれたピクセルの色を決定します。
平面は頂点が3つあれば決まることより、基本的にシェーダーでは 3頂点がそろうことで一つの平面が描かれます 4。3Dモデルでは複雑なものでも基本的にすべて三角形で描かれることになります。この三角形を利用して、三角形内部のピクセルを補間します。補間は、頂点シェーダーからピクセルシェーダーに渡される値が頂点間でなめらかになるように行われます。
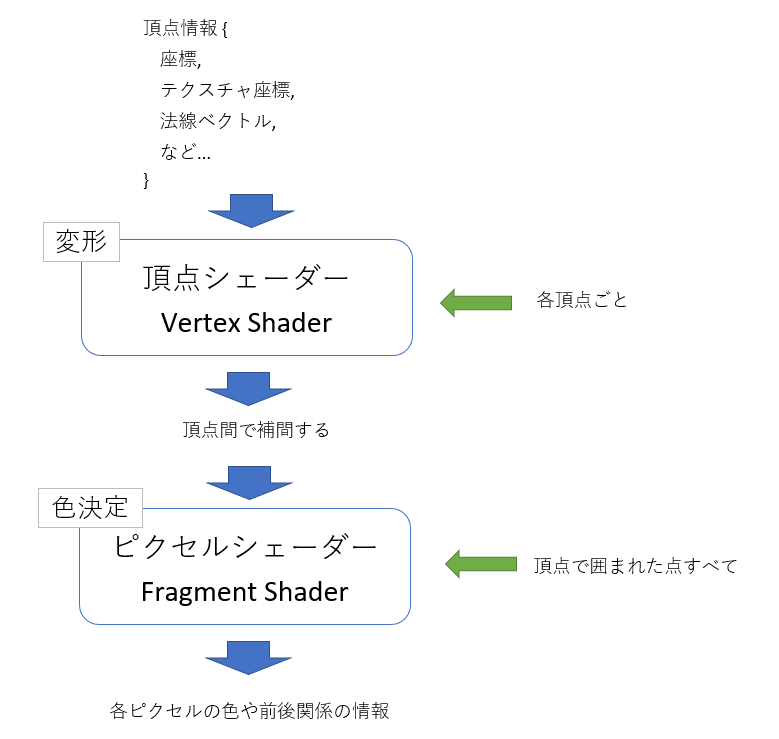
2つのシェーダーとシェーダーに渡すデータをまとめると次の図のようになります。
色は、頂点シェーダーから渡された補間値を使ったり、3Dモデルに張り付けるテクスチャ画像から抽出したり、さらにそれに陰影を付けるなどをして決定します。つまり、ピクセルシェーダーの仕事は、テクスチャ画像からの色の抽出や、陰や影を付けたりといった処理ということになります。
もし、3頂点について座標と色を渡すと、両方に関して補間された値がピクセルシェーダーに渡されます。試しに「赤い頂点」、「緑の頂点」、「青い頂点」を渡すと、次のように描画されます。
[
# [座標, 色],
[[ 0.0, 0.5], [1.0, 0.0, 0.0]],
[[-0.5, -0.5], [0.0, 1.0, 0.0]],
[[ 0.5, 0.0], [0.0, 0.0, 1.0]],
]
頂点間に関しては補間された色になっていることがわかります。繰り返しになりますが、補間は色に関してだけではなく、頂点座標やそのほか頂点シェーダーからピクセルシェーダーに渡されるすべての情報について行われます。ちなみに補間ではなく定数を渡したい場合などは、頂点シェーダーからピクセルシェーダーに渡すのではなく、フロントのプログラムから直接 Uniform な値として渡すのが定石です。
3頂点について座標と平面に適用するテクスチャの座標を渡し、ピクセルシェーダーにてテクスチャサンプリングを行うようにすると、テクスチャを平面に合うように変形させて表示させることも可能です。
[
# [座標, テクスチャ座標],
[[ 0.0, 0.5], [0.0, 0.0]],
[[-0.5, -0.5], [0.0, 1.0]],
[[ 0.5, 0.0], [1.0, 0.0]],
]
この節で解説した内容は、 WebGLの基本 の次のページで詳しく解説されています。
3次元描画特有の問題
ここで3次元に話を戻すと、3次元っぽく2次元平面にオブジェクトを描画するために位置を変形させられた頂点を骨格として、その中を塗りつぶすことで3次元っぽく描くということになります。ここで問題になってくるのは、 描画されない隠れる部分がある ということです。
とても簡単な例は立方体です。
この図について、真ん中に示すように面Aのほうが前方にあるように描画をしたいとします。もしここで何も考えず面A → 面Bというように描画してしまうと、一番右に示すみたいに面Bのほうが前方に描かれてしまいます。
全てのオブジェクトについて描画前に面の描画順序を決めることでも解決できそうですが、とても難しそうです。そこで2つの考え方からこの問題に取り組みます。
描画する平面としない平面
そもそも、面Bは描画したい面なのでしょうか? 今回の場合、本当に描画したい立方体は次のようなイメージになると思います。
面Bは全く描画されていません。面Bはカメラに対して「完全に裏側を向いている」面です。実はこのような面は次のルールを適用することであぶりだすことが可能です。
- カメラからみて、3頂点の座標を渡された順に見ると反時計回りになっている面を表とし、描画する
時計回りでも同じことができますが、とにかくシェーダーに頂点を渡す順番を一つの回り方に定めます。すると、決めた回り方と反対回りで渡されるときは「裏を向いている」ことがわかるのです!
頂点の順番は立方体のモデルを作成する際に指定できます。カメラに向いている面が表になるように反時計回りに頂点を渡すようにしましょう。
面Aが表を向いているとき面Aを構成する頂点は反時計回りになっている一方、面Bの頂点はカメラからみて時計回りになり、描画対象ではないことがわかります。このようにして、描画対象から面Bを外すことができます。
深さで描画を制御する - 深度バッファ
前の方法で対策をとっても、以下のように「描画される面同士」の場合は矛盾が起きてしまう可能性が残っています。
水色の面 → 赤い面という順番で描画される場合は問題ありませんが、赤い面の後に水色の面が描画されると右図のような現象が発生します。ここまでもったいぶりましたが、これを回避する方法はいたって単純です。「面の位置する深さ」、すなわち頂点のZ座標から得られる深さを保存しておき、上書きされそうなときにより手前にあるほうのピクセルを残せばよいのです。(つまり面の描画順を決めたりはしません。)
そのために、色情報だけを保存するのではなく、深さも同時に保存しておく必要があります。その保存領域は深度バッファとして用意します。これはフロント側での仕事で、GLSL側では頂点シェーダーの段階でZ座標を含めた適切な情報を gl_Position 変数などに渡せれば問題ないはずです。
ここまで紹介した話題の関連リンクです。
次の節以降もピクセルシェーダー関連の話題ですが、少し重いので、ピクセルシェーダーとしての節はここで終了とします。
3. 光の導入
シェーダーの各段階におけるトピックをそれぞれ説明してきましたが、まだここまでの知識では3Dモデルを描画してものぺっとした感じになります。理由は単純で、ライトについて何も考えていないので面が単調で、立体感が損なわれているためです。
Unityにも太陽(ライト)があるように、3DCGを行う場合は光源を設定し、光源から発せられる光が反射したことで3Dモデルの色が描画されているように見せかける必要があります。本当に光が反射しているようにシミュレートする技術である「レイトレーシング」が最近は話題ですが、(最新の強つよグラボならなんとかなるでしょうが...)こちらは計算が重いので今回はやめておきましょう。
レイトレーシングの代わりに、Phongの反射モデルを使って疑似的に光の影響をシミュレートする手法を取ります。このモデルでは、光とオブジェクトの間で次の3要素について考えます。めちゃくちゃ乱暴に言うと次のような感じです。
- 環境光: 全体的な明るさ
- 反射光: オブジェクトの色
- 光沢: オブジェクトにうつる反射された光源。光沢のようになる。鏡のようなイメージ
青い球体を描画しつつ、詳しく見ていきます。
環境光 Ambient Light
暗い部屋で電気をつけると全体が明るくなります。この時、光の方向などに関係なく基本的には一様に明るくなるかと思います。これは、光源から出た光があらゆる場所に乱反射した結果起こる現象だそうです。
この一定に明るくなる光を描画します。3DCGでは「全体について5最低限これぐらい明るくしたい・明るくなる」みたいな位置づけだと思います。
後述しますがオブジェクトにはマテリアルというものがくっついていると考えます。このマテリアルには、色や使用するテクスチャなどの情報があります。マテリアルが持つ環境反射係数 $k_a$ と環境光の強さ $i_a$ (ともに3次元ベクトルです。それぞれの要素を掛けます。以降ドット積ではないものはすべて要素ごとの積(アダマール積)とします。)より、環境光によって加算される分の色 $C_a$ は次の通りです。
C_a = k_a i_a
以下環境光のみがあった場合のイメージです(薄暗くて申し訳ありません...)
反射光 Diffuse Light - 陰を付ける
ここからは光に方向性があるものとして議論を進めていきます。
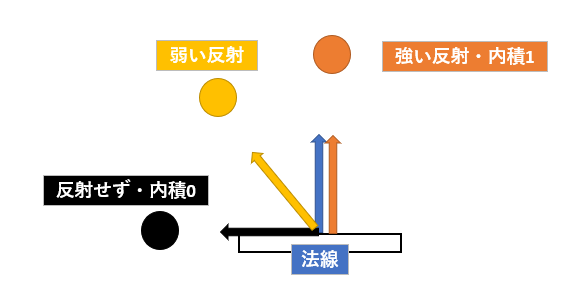
光線が反射することでオブジェクトが見えるとします。面が光線に対して垂直なときに明るく、面と光線が平行なときは暗くなることは想像に難くありません。
面が斜めの時はその中間になるようにするだけで、なんと3Dっぽく見えてしまいます。これが反射光(Diffuse Light)です。
面の向いている向きを法線ベクトル $N$ 、光線方向の逆ベクトル(オブジェクト表面から光源に向かう向き)を $L$ とし、両方のベクトルの大きさを1とすると( normalize 関数などを使うことで大きさを1にできます。)、面と光線のベクトルの内積が最もこの用途に適しているでしょう。
環境光と同様に光源ごとに設定されている光の強さを $i_d$、マテリアルが持つ拡散反射係数を $k_d$ とすると、光源ごとの反射光によって加算される分の色 $C_d$ は次の通りです。
C_d = k_d (L \cdot N) i_d
以下反射光のみがあった場合のイメージです
ちなみにこの反射光によって「陰」が表現できたことになります。ここでいう「かげ」は、物体にあたる光の量が異なることで生じる明暗のことです。一方、同じ読み方をする「影」、すなわち複数の物体間で起きる光がさえぎられることによって生じる明暗は、「複数の物体と光源」の相対的な位置関係から決定されるので、今解説したような単純な仕組みでは実装できません。これについては後の節で再び触れたいと思います。
反射光については、次のページが参考になります。
光沢 Specular Light
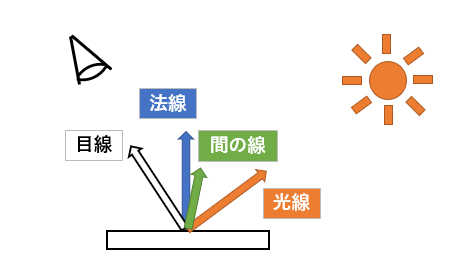
つやつやした面には、光源の光が強く反射される点がありテカって見えます。いわゆる光沢は、光線がオブジェクト表面にて反射して直接目に入ってくるという場合に強くなるものです。すなわち、下の図のように、目、光源、面の法線の関係で強さが決まります。
反射光の時とは違い、光線そのものではなく、目線と光線の中間にあたるベクトルと法線の内積で強さを決めます。反射光に少し似ていますが、「光源そのものの鏡による反射」と考えると(反射という文字列が入っていてややこしいですが...)違うイメージが持てるかと思います。
ここまでと同様に光源ごとに設定されている光の強さを $i_s$、マテリアルが持つ鏡面反射係数を $k_s$ とし、中間ベクトルを $H$ 、光沢感を出すために設定する内積を累乗する回数を $\alpha$ とすると、光源ごとの光沢によって加算される分の色 $C_d$ は次の通りです。
C_d = k_s (H \cdot N)^{\alpha} i_s
以下光沢のみがあった場合のイメージです(暗くて申し訳ないです...)
光沢は目線の移動の影響を強く受けるので、ゲーム内で目線が動く時に立体的に感じさせる効果が期待できそうです。
光沢については次のページが参考になります。
これらの和
そしてここまで紹介した3要素の合計が表面の色 $I_p$ になります。Phongの反射モデル - Wikipedia によると最終的に以下のような式となります。(光沢のみ少し計算方法が異なります。)
I_p = k_a i_a + \sum_{すべての光源} \left( k_d (L \cdot N) i_d + k_s (H \cdot N)^{\alpha} i_s \right)
全ての要素を足すと次のように描画されます。...設定が甘いせいで光沢が全然ないですがご容赦ください...
以下参考になるページです。
4. Objファイルを覗いてみる
ここまで紹介した話題は実はObjファイルの中身を理解するためのものであったりします。というわけで、いよいよObjファイルを読み解いていこうと思います!
Blenderを立ち上げたときにデフォルトで表示される立方体に緑色のマテリアルを付与し cube.blend という名前で保存後、それを .obj 形式でエクスポート※します。すると以下のようなObjファイルが得られると思います。
※ ここまでの話と矛盾がないように、ジオメトリ → 三角面化にチェックを入れて エクスポートしています。普通にエクスポートした場合は三角面化されておらず f 命令に渡される頂点数が4つになっているかと思います。
# Blender v2.83.5 OBJ File: 'cube.blend'
# www.blender.org
mtllib cube.mtl
o Cube
v 1.000000 1.000000 -1.000000
v 1.000000 -1.000000 -1.000000
v 1.000000 1.000000 1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 1.000000 -1.000000
v -1.000000 -1.000000 -1.000000
v -1.000000 1.000000 1.000000
v -1.000000 -1.000000 1.000000
vt 0.875000 0.500000
vt 0.625000 0.750000
vt 0.625000 0.500000
vt 0.375000 1.000000
vt 0.375000 0.750000
vt 0.625000 0.000000
vt 0.375000 0.250000
vt 0.375000 0.000000
vt 0.375000 0.500000
vt 0.125000 0.750000
vt 0.125000 0.500000
vt 0.625000 0.250000
vt 0.875000 0.750000
vt 0.625000 1.000000
vn 0.0000 1.0000 0.0000
vn 0.0000 0.0000 1.0000
vn -1.0000 0.0000 0.0000
vn 0.0000 -1.0000 0.0000
vn 1.0000 0.0000 0.0000
vn 0.0000 0.0000 -1.0000
usemtl Material
s off
f 5/1/1 3/2/1 1/3/1
f 3/2/2 8/4/2 4/5/2
f 7/6/3 6/7/3 8/8/3
f 2/9/4 8/10/4 6/11/4
f 1/3/5 4/5/5 2/9/5
f 5/12/6 2/9/6 6/7/6
f 5/1/1 7/13/1 3/2/1
f 3/2/2 7/14/2 8/4/2
f 7/6/3 5/12/3 6/7/3
f 2/9/4 4/5/4 8/10/4
f 1/3/5 3/2/5 4/5/5
f 5/12/6 1/3/6 2/9/6
# で始まる行はコメントです。使用したBlenderのバージョン等が書かれています。 mtllib cube.mtl はマテリアルについて記述したファイルを指定しています。
v 命令によって頂点座標が記述されています。
v 1.000000 1.000000 -1.000000
ここでは頂点座標を宣言しているだけのようなものであり、これ自体はまだ「描画するための頂点情報」としては不完全です。
v 命令ブロックの次のブロックでは vt 命令でテクスチャ座標を宣言しています。
vt 0.625000 0.500000
これも後ほど使うために宣言しているのみで、この情報単体では意味を成しません。
3つ目のブロックでは、 vn 命令によって面の法線を宣言しています。法線は反射光を実現するのに必要不可欠なのでした。
vn 0.0000 1.0000 0.0000
そして、この3つの宣言を用いて、描画する頂点を指定することで面を記述しています。 面がもつ3つの頂点を順番に渡せば シェーダーが面を描画してくれるのでした。
f 5/1/1 3/2/1 1/3/1
それぞれの頂点情報は使用する 座標番号/テクスチャ座標番号/法線番号 が指定されています。上で宣言された要素と番号が1始まりで対応しています。面の持つ頂点は、表を向いているときに反時計回りになるように宣言されているはずです。(多分...確かめた限りでは)
これらの頂点情報を用いることで、「面の向き」と「法線」が6得られるので、反射光を含めた3DCGがようやく描けそうです。そして、あとは色の情報が必要です。これはマテリアルをまとめた .mtl ファイルのほうに記述されています。
# Blender MTL File: 'cube.blend'
# Material Count: 1
newmtl Material
Ns 323.999994
Ka 1.000000 1.000000 1.000000
Kd 0.000000 1.000000 0.000000
Ks 0.500000 0.500000 0.500000
Ke 0.000000 0.000000 0.000000
Ni 1.450000
d 1.000000
illum 2
マテリアルファイルには、今回は書かれていませんがテクスチャ情報(テクスチャ画像の名前)や、先ほど光の導入で解説した各種係数が記述されています。 Ka は $k_a$、 Kd は $k_d$、 Ks は $k_s$ に対応しています。
これらの情報を読み込んで、どう使うかはフロントとシェーダーの記述次第です。Objファイルのロードは結構ライブラリが落ちているみたいなので、探してみると良いと思います。Rustの場合はpistonが提供しているものやtobjというライブラリがあります。
- PistonDevelopers/wavefront_obj: A parser written in rust for the wavefront .obj file format.
- tobj - Rust
私はtobjの方を使用しています。
以下にこの節の関連リンクを載せます。(まるぺけの方はObjファイルではなくFBXファイルに関してですが、参考にはなると思います。)
5. 影を付ける - Shadow Mapping
Objファイルとはもうあまり関係のない話題ですが、姉妹記事のほうで取り組んでいるためこちらで原理を解説します。
反射光 Diffuse Light - 陰を付けるのところで解説した通り、シェーダーにおいて影は陰と比べて描画するのが難しいです。なぜなら、ここまでで解説した頂点情報が渡されても、他のオブジェクトとの関係をシェーダーは知らないので、シェーダーだけの力では描画できないからです。フロントとの協力が必要になってきます。難しそうですね。
でも実は今回紹介するシャドウマッピングという手法は言葉として説明すると意外とシンプルです。
- 影の原因となる光源の立場から見る。光源の座標に立ち、ある物体を見ると、その物体の後ろ側は見えない。光線からすれば光が届かない場所であるから、他の場所から見ると、その後ろ側は影になっているはずである。
とはいえ言葉だけだと難しいので映像を使おうと思います。最初のほうで描かれている白い点が光源位置とします。影が見えている状態からこの白い点に移動し、オブジェクトを光線目線から見てみると、影がすっぽりとなくなっていることが観測できると思います。
つまり、最後に示した次の "写真" と、座標との対応を何かしらの方法で事前に取得しておけば、どこが影になるかを判別することができます!
この写真を用いた影生成手法を深度バッファシャドウと呼ぶそうです。もう少し詳しい原理はまるぺけさんのサイトを見ていただければと思います。
言うのは簡単だけど実際に行うのは難しい...というのがこの手法のイメージです。この記事は原理の紹介にとどめるものですから、言うだけ言いました(笑)
ちなみに、Rustでの実装では次のプロジェクトを参考にしました。参考までに。
あとがき
ここまで読んでいただきありがとうございました!具体的な実装方法などが書かれていなかったため雰囲気ぐらいしか出せなかったかもしれませんが、3DCGの雰囲気だけでもこの記事から読み取っていただけたならば幸いです。
コメントや編集リクエスト等ありましたら是非お願いいたします。
-
この箇所に限らず記事全体について、解説のしやすさを優先し、思い付きで記述しているので、多分に間違いを含んでいる可能性がありますが、ご了承ください。間違いとしてひどいと思われるものがあれば気軽にコメントや編集リクエストをください! ↩
-
この座標系は左手系となります。詳しくは調べていませんが、3DCGでは、右手系左手系どちらについても使われることがあるようです。 ↩
-
もっともUnityを捨てている時点で車輪の再開発ではあります。要はそこに主眼を持たないならばという意味です。 ↩
-
設定次第では四角形で描画することもできますが、本記事では扱いません。 ↩
-
記事ではお茶を濁していますが、 $i_a$ は各光源のもつ強さの合計を使用しても、定数として設定してもどちらでも良いかと思います。実装方法次第です。私は合計になるような形で実装しました。 ↩
-
数学的には面の向きと法線は同意義かもしれませんが、ここまでで解説した通り、面の向きは描画対象である表向きを検出するためのみ、法線は反射光を返す強さを決定するために用いられ、つまり用途が異なります。一応念のため。 ↩