ワールドルールテトリスの作り方またはRust入門した感想的な何か

こちらは大学で所属しているゲーム制作サークルの会誌にあてた記事です。テトリスを我流で何度か作ってきたので、「どうすればテトリスを作成できるか」をまとめました。...といいつつも、Rustの紹介もしているのでかなりかなりかなり読みにくい文章です。あらかじめご了承ください。

ここから遊べます!!!!!↓(IE、Edge非対応、スマホ対応)

完成したテトリスのデモ(Pistonのほう)↓

Githubレポジトリ:

ライブラリ: https://github.com/anotherhollow1125/tetris_by_rust_lib
Piston: https://github.com/anotherhollow1125/tetris_by_rust
Wasm: https://github.com/anotherhollow1125/tetris_by_rust_wasm

Tスピン判定以外はワールドルールに準拠しています。

使用した言語とその理由

タイトル通り今回のテトリス制作にはRustを使用しました。ライブラリにはPiston (https://github.com/PistonDevelopers/piston) を使用しました。筆者がRustの勉強を始めたのは今年の夏休みで、タイトル通り入門したてホヤホヤです。

Pistonでの実装後、せっかくなら他の人に 遊んでもらいたい と考え、WebAssemblyにもしました。これに一週間もかかってしまった...ワッサン🥐...¹ちなみにWebAssemblyにするにあたり Tutorial - Rust and WebAssembly (https://rustwasm.github.io/docs/book/game-of-life/introduction.html) というページがものすごく参考になりました。英語の記事ですがとても読みやすかったです。ライフゲームをブラウザで動かすチュートリアルです。

話を戻します。なぜRustを選んだかというと、最近話題だからという以上に、RustはPistonのGuide (https://github.com/PistonDevelopers/piston/blob/master/GUIDE.md) にも書いてある以下に示す ゲーム制作という観点で有利な点 が多々あったからです。

ガベージコレクションを使用しない

普段はUnity C#等でゲーム制作を行っていますが、C#やJavaといったモダンなプログラミング言語にはガベージコレクションがつきものです。GCが標準にはない言語はC言語かC++ぐらい²じゃないでしょうか？

普通のゲームを作成する場合は別にGCが働いたぐらいでは(GCが大量に働くような書き方をしない限り)パフォーマンスに影響はないと思われますが、 テトリスを作ったとして、例えば強化学習してみたい とか思ったりしませんか？(いきなり出る意識高いワード)

筆者は以前、Nimでテトリスの動的ライブラリを作成しPythonで強化学習した³ことが実際にあったのですが、そのときにガベージコレクションでかなり悩まされました。

強化学習させるにはかなり高速に回数をこなさせる必要があります(別に速度は重要ではないですが、現実問題としてです)。毎回GCが少しでも働くように書いてしまうとかなり遅くなります。結果として、せっかくNimというモダンな言語を使用しているのに、インスタンスや動的配列等を極力使いまわすように書かなければならないという、かなりの苦痛を味わうことになったのでした。

Rustにはガベージコレクションなしでも動的配列等を安全に扱う仕組みである 所有権とライフタイム があります。

今後またテトリスの強化学習をさせたいと考えたときに、GCを使わない方法で実装されたテトリスのライブラリがあればかなり楽になると考え、Rustで書いてみることにしました⁴。

便利な列挙型がある&Null安全

Scala等のモダン言語だとよくある機能なのか、筆者には経験が足りないのではっきりとはわかりませんが、 他の型を内包できる列挙型とそれを便利に扱えるmatch式 があります。

例えば今回実装したホールドでは、

Rust

enum Hold {
    Holding(&'static Mino),
    None
}

のように書いています(Minoというのはテトリミノを意味します)⁵。テトリスではゲーム開始直後にはホールドがありません。持っているか、持っていないかの2状態を表すので他の言語ではブール型を使用してもいいかもしれませんが、この列挙型のおかげで 持っているか という情報と 何を持っているか という情報を統一化できるため、より直感的に、より安全にホールドを実装することができます。

ちなみにホールド周りの処理は以下のようになってます。

Rust

let mino = match self.holdmino {
    Hold::Holding(mino) => mino, // ホールドしていたミノを返す
    Hold::None => {
        self.nextminos.push_front(self.minogen.generate()); // Nextにミノを充填する
        self.nextminos.pop_back().unwrap() // Nextから取ってきてミノを返す
    }
};
self.holdmino = Hold::Holding(self.contmino.mino); // 降っていたミノをホールドする
self.game_over = !self.drop_start(mino); // 降らせることができなければゲームオーバー
self.holdflag = true; // ホールドが次のミノが降り始めるまでできないようにするためのフラグ

matchが式であるというのも良い点です。とても直感的にコードを書くことができています。

match式の機能についてこれ以上詳しくは述べませんが、記述漏れがあったりするとコンパイルエラーになってくれたりと、かなり便利です。

Option型という標準の列挙型もあり、Rustの列挙型はNull安全を保つための強い機能となっています。

C言語のライブラリを使用できる、低レイヤーからいじれる

今回は使用しませんでしたが、描写のライブラリにSDL2が使える等、既存のC言語ライブラリが使えるという強みを持っています。

ライブラリを容易に作成できる

Rustの管理を一通り行ってくれる機能Cargoのおかげで、ライブラリ等を楽に記述&使用可能です。筆者には詳しく書くだけの力量がないです()
ただ絶対に一つ言えるのは、C言語書いたことがある人ならライブラリの記述のしやすさに驚きます。階層構造等に強く、ファイルの整理が容易です。

正直個人的にはPythonと同等か複雑なライブラリならPython以上に記述しやすいように感じました。

UFCS記法と理解が容易なオブジェクト指向

JavaやC#のようなクラス型オブジェクト指向、別に悪いとは思いませんが、最近のモダン言語では取り入れられていない機能であるような気がします。(偏見？)

Rust、Nim、Go、Pythonなどの言語⁶では、「構造体を型とみなし 関連関数 (他の言語で言うクラスメソッド)を実装する。インスタンスメソッドは第一引数を構造体にすることで実装する」という形のオブジェクト指向を採用しています。 hoge.method() のような書き方は UFCS記法 (Unified Function Call Syntax) というシンタックスシュガーで、実際は Hoge::method(hoge) という風に「ただの関数を呼び出し、構造体を渡している」のです。(Pythonでも同じです。Hoge.method(hoge) を試してみてください。)

こうすることで構造体は ただの型 になります。クラスじゃないのでかなり幅広い書き方が可能になります(多分)。個人的にはこのしくみは理解しやすいので好きです。

クラス型オブジェクト指向の継承の代わりとしては トレイト があります。大規模なゲームではトレイトも必要になってくるでしょうが、テトリスみたいな小さなゲームでは不要でしたので、重要な機能ではありますが説明を省きます。

関数型言語ライクなイテレータの扱い方

Unity C#やってる人ならLINQって言ったほうが伝わるかもしれないあれです。C#でLINQ使うとどうパフォーマンスに影響するかはよく知らないですが、要は関数型言語にある map とか filter とかが使いやすい上に使ってもパフォーマンスに影響しない(一説によるとむしろ向上する)よという話です。

例えばラインチェックの場面などで使えます。

for i in 0..21 {
    if self.field[i][1..11].iter().all(|b| b.filled) {
        // ラインクリア用の処理
    }
}

ここでは all 関数に無名関数を渡しライン上のすべてのブロックが満たされているかを確認しています。

よりよい例は公式ガイドが詳しかった&分かりやすかったのでリンクを載せておきます。

• 一連の要素をイテレータで処理する - The Rust Programming Language https://doc.rust-jp.rs/book/second-edition/ch13-02-iterators.html

• パフォーマンス比較: ループVSイテレータ - The Rust Programming Language https://doc.rust-jp.rs/book/second-edition/ch13-04-performance.html

長々と紹介してきましたが結局のところ、「ゲーム制作においてパフォーマンスを求められる場面で使えそうな言語で、C++じゃないものとしてRustが使えるのではないかと考えた」というのがRustを使った理由という感じです。

本題　テトリスの作り方

テトリスの技術記事のはずがなぜまだよく理解していない言語の紹介になってるんだ()

ここからは普通にテトリスの実装の話です。必要な機能の考察が中心なので、方針としてソースコードはあまり書きません。全体を見たい方は Githubレポジトリ (https://github.com/anotherhollow1125/tetris_by_rust_lib) をぜひご覧ください。

本記事でテトリスの実装方法の全てを語るつもりはありません。個人的にこれは紹介したいというテトリス実装の考え方を書き綴っています。

またタイトル通りワールドルールに準拠するための考察が多数を占めています。ワールドルールについては以下に示すTetrisちゃんねる様のサイトがとても詳しいです。

Tetrisちゃんねる Rule (https://tetrisch.github.io/main/rule.html)

テトリミノについて

定義

一つの実装方法として思いつくのは、列挙体として定義する方法です。

Rust

enum MinoKind {
    I, O, S, Z, J, L, T,
}

しかし今回のRust製テトリスでは、 Mino 型の構造体を定義し、それを使う形になりました。列挙体をうまく利用して書きたかった...うーん

Rust

struct Mino {
    shape: [[bool; 4]; 4],
    size : usize,
    color: [f32; 4],
}

const PURPLE: [f32; 4] = [0.5 , 0.0 , 0.5 , 1.0];

// Minoインスタンスの一例
static T: Mino = Mino {
    shape: [
        [false, true , false, false],
        [true , true , true , false],
        [false, false, false, false],
        [false, false, false, false],
    ],
    size : 3,
    color: PURPLE,
};

「参照するだけ」という定数的扱いをしたかったので運用時はすべての型記述で &'static Mino としました。これ以外に static は使用していません。

まぁ要は「形、大きさ、色」を一緒に扱えるとこの先便利ということです。

コードゴルフしてるようなテトリスだと形がわからないような記述になったりしてますが、ここを横着せずともテトリスはちゃんとできます。直感に従いましょう。

テトリミノの向き

次に現在落下中のミノの回転に伴う方向について考えてみます。 これらもまずは列挙体を考えます 。上右下左とは区別するために、北東南西で記述しています。以降この向きを方角と呼びます。

Rust

enum Dir {
    North, East, South, West,
}

列挙体で考えるべき理由は2つあります。

まず十分条件的な意味として、「衝突判定時」と「描画時」以外の時は、現在動かしているテトリミノの情報は不要だからです。
言い換えると、「現在動かしているミノの情報を1マスずつ配列か何かに保存しておく必要性はない」という意味です。

判定時、描画時にフィールドに投影してみればよいということです。そのための現在操作中のミノを扱う構造体の一例が以下です。

Rust

struct ControlledMino {
    pos   : (i32, i32),
    mino  : &'static Mino,
    dir   : Dir,
}

つまり「左上の座標、扱ってるミノの種類、方角」の3つさえあれば十分という意味です。

パフォーマンスに問題がない言語(Rustなら無問題ですし多分Pythonぐらいの言語でも問題なし)ならば、この3情報から比較や描画の都度描画用の配列を作るのでなんの問題もありません。書きやすさを優先しましょう。

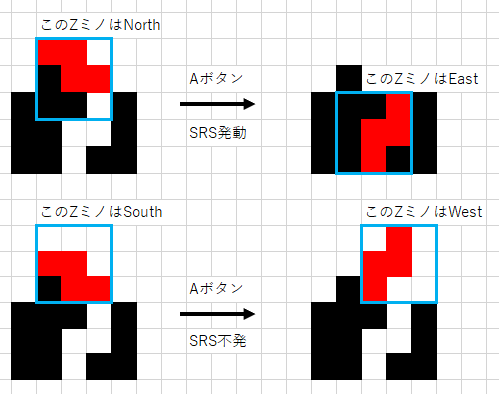
2つめの理由は必要条件的なものです。それは「ワールドルールでは方角によって適用される回転規則が異なる場合がある」からです。

最も決定的なのはSブロックやZブロックでしょう。以下の図はスーパーローテーションシステム(SRS)を実装した場合の挙動の話ですが、テトリス上級者なら体験したことがあるのではないでしょうか？

そうです、見た目が同じでも方角によって結果が変わる場合があるのです！

となると仮に現在操作中のミノの配置を常に何かしらの配列で保存する方針で行くにしても、ワールドルールを適用したい場合は結局方角『も』保存する必要が出てきます。これが必要条件と言った意味です。

なら、最初から方角だけ保持しておけばいいということになります。

操作中ミノのブロックの取得方法

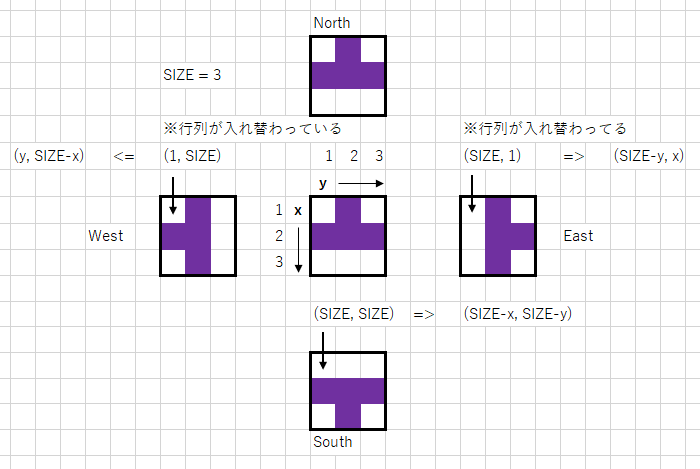
ミノの種類と方角、大きさをバラバラにしたところで、判定時、描画時にどのようにブロックを取得すればいいのでしょうか？図のように考えましょう。

それぞれ取得時にどのブロックがどこに行くかを考えます。左上のマスにまず注目して考えると分かりやすいです。インクリメントに従い参照されるブロックの位置がどう変化するかに要注意です。(East West だと軸が入れ替わっていることに注意しましょう。)

図をもとにそのままコード化します。ブロックが入ってる箇所が真となる二次元配列を返す関数です。

Rust

fn rend_mino(&self) -> Vec<Vec<bool>> {
    let size  = self.mino.size;
    if size < 1 { return vec![]; }
    let shape: [[bool; 4]; 4] = self.mino.shape;
    let mut method: Box<dyn FnMut(usize, usize) -> bool> = match self.dir {
        Dir::North => Box::new(|i, j| shape[       i][       j]),
        Dir::East  => Box::new(|i, j| shape[size-1-j][       i]),
        Dir::South => Box::new(|i, j| shape[size-1-i][size-1-j]),
        Dir::West  => Box::new(|i, j| shape[       j][size-1-i]),
    };
    (0..size).map(|i| {
        (0..size).map(|j| method(i, j)).collect()
    }).collect()
}

取得用関数を方角ごとに用意し、それを使ってあたかも向きを変更させたかのように取得します。Rustの場合のクロージャの型ですが、各関数のメモリ上の大きさがわからない(=実行時ヒープ領域に保存される)ので、 Box という構造体を用いてやり取りしています。

フィールドの設定

すでに固定されたブロックを記憶しておく方法について、流れ的に一応言及しておきます。入門書系テトリスだとまず最初にフィールドについて考えるような気がします。

覚えておくべきは「満たされているか」と「色」の二点だけです。それで十分です。(パブリックにしておくと描画時に多少楽になる可能性があります。こだわる人はゲッターを書いてもいいと思います。)

Rust

pub struct Block {
    pub filled   : bool,
    pub color    : [f32; 4],
}

これだけに限定しろという意味ではないです。例えばラインクリア時にエフェクトを掛けたいときなどにエフェクトの対象であるかを把握するブール値があったりしてもいいでしょう。

フィールドは、入門書系テトリスに従うと22ライン×12ブロックであることが多いように感じます。テトリスは21×10(20ラインではなく21ラインです。見えないラインが最上部にあります⁷。これだけは変わりません。)であるはずなのでこれは妙ですが、外側に衝突判定用のダミーブロックを置くための処置です。

後述する衝突判定の処理の実装次第では21×10でも問題ないです。慣例に従い自分は今回も22×12で記述してますが、正直21×10で書いたほうが楽な気が最近はしています。

結局、形状としては次のような感じになるでしょう。

field: [[Block; 12]; 22];

ここで座標についても考えましょう。配列の並び順に合わせ、垂直下向きをx(またはi)方向、水平右向きをy(またはj)方向と定めると、経験則的に自然にコーディングが可能です。行列と同じです。

field[x][y] == x行y列にあるブロック

ただしこの場合ウィンドウ等に描画する際はx軸とy軸が逆になることに注意してください。

衝突判定

移動時と回転時において衝突判定が必要です。2つの方法が考えられます。

• 移動、回転前に隣接するブロックを調べることで衝突しているか(すなわち移動、回転可能か)調べる
• 先に移動、回転を試みて、ダメだったら(他のブロックと重なっていたら)戻す

1つめの方法のほうが直感的ですが、一体どこのブロックについて調べればいいのかがはっきりしません。例えば右に移動するならば操作中のテトリミノの右側を見ることになりますが、下に移動する際は右を見る必要はないです。また、操作中ミノの範囲を3×3で捉えたとして、衝突する可能性があるブロックがすでにその範囲内に入っているかもしれません...

...とこのように考えていくと、少しむず痒く感じる方もいらっしゃるかもしれませんが、2つめの方法のほうが実装がかなり容易であることがわかります。

ちなみに衝突判定はブロックが存在する場所だけでおｋです。...何を当たり前のことを言ってるんだと思われるかもしれませんが、例えば「ControlledMino構造体の左上座標が負値になってしまっているかなんてみなくていい」という意味です。ここで下手に調べなくていいところまで調べて衝突として判定してしまうと、「スキマが空いているのに移動が行えない」などの悲惨な結果になりかねないです。その意味で、ブロックで埋まっている箇所だけ調べましょう。

Rust

fn pos_verify(&mut self, field: &[[Block; 12]; 22]) -> bool {
    let r = self.rend_mino(); // 形状取得
    let size = self.mino.size;
    for i in 0..size {
        for j in 0..size {
            if !r[i][j] { continue; } // 埋まってない場所に興味はない

            let (x, y) = self.pos;
            // 範囲チェック
            let (x, y) = ((i as i32 + x) as i32, (j as i32 + y) as i32);
            if x < 0 || 21 < x || y < 0 || 11 < y { return false; }
            let (x, y) = (x as usize, y as usize);
            // 設置可能チェック
            if field[x][y].filled { return false; }
        }
    }
    true
}

移動関連

先程出した「操作中のテトリミノの情報を格納する構造体」( CntrolledMino )の左上座標を変化させれば良いだけです。移動用に関数を定義し、衝突判定で述べたとおり、移動後もしすでに設置されたブロックと重なっていたら、戻すように処理を書きます。関数の返り値として移動が完了したかのブール値を返すようにしておくと、後述のSRSや固定処理を楽に記述できるようになります。

Rust

fn move_mino(&mut self, field: &[[Block; 12]; 22], i: i32, j: i32) -> bool {
    let pre = self.pos; // 以前の座標を記憶する
    self.pos = (self.pos.0 + i, self.pos.1 + j); // 移動してみる
    if !self.pos_verify(field) { // ダメだったら
        self.pos = pre; // 戻して
        return false; // 移動できなかったことを知らせる
    }
    true // 移動が完了したことを知らせる
}

これに関連して、ハードドロップの機能を予め作成しておくとよいです。下に移動できるだけ移動させ、強制的に固定するという、言葉にしてみるとそれだけの処理です。恐れることはありません。

回転関連　スーパーローテーションシステム(SRS)

いわゆるTスピンだとか先ほど紹介したZミノの回転入れだとかそういう関連の話ですが、 実はただの左上座標の移動なので記述量は多いもののそこまで大変ではありません。

...と言い切ってしまうほど簡単ではないんですけどね、SRSについては先にも紹介したTetrisちゃんねる様が一番参考になります。

Tetrisちゃんねる SRS (https://tetrisch.github.io/main/srs.html)

SRSを実装しない場合は移動のときとほぼ処理は同じです。今回は方角の方を変更してみて、もし衝突していたらもとの方角に戻します。

SRSの処理は方角変更後の判定中に入れます。(移動->判定)->(移動->判定)...を試し、全ての移動について失敗したら方角を戻すように実装します。難しいこと(中心軸の移動、とか言われたりしてます)をしているように見えて、実は座標を少し変えてただけなんですね。

Tetrisちゃんねる様のサイトに書いてある情報を改めて一応ここに書いておきます。

T、S、Z、L、J ミノ

1. 回転してみる
2. 座標を左右に動かしてみる
   • 回転後East: 左に移動
   • 回転後West: 右に移動
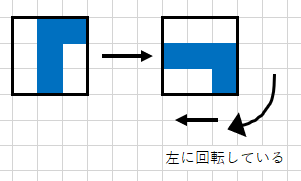
   • 回転後North or South: 回転した方向の逆へ移動。例えばEast -> Southなら左に回転している(図を参照)ので右に移動
3. 2の状態から座標を上下に動かす
   • 回転後East or West: 上
   • 回転後North or South: 下
4. もと(1の状態)に戻し座標を上下に2マス動かす
   • 回転後East or West: 下2マス
   • 回転後North or South: 上2マス
5. 4の状態から座標を左右に移動。移動の方向は2と同様に考える

Iミノ

※ Tetrisちゃんねる様のサイトの「図」のほうに合わせた解説です。図と下に書かれた考察で相違があるようです。実装時は深く考えず図を見ながら機械的に記述したほうが楽です。

1. 回転してみる
2. 軸を左右に動かす
   • 回転前North: 左の壁にくっつく(例えば回転後Eastなら2マス、回転後Westなら1マス左に移動)
   • 回転前East: 回転後Northなら右2マス、Southなら左1マス
   • 回転前South: 右の壁にくっつく
   • 回転前West: 回転後Northなら左2マス、Southなら右1マス
3. 1に戻し反対側を考える
   • 回転前North: 右の壁にくっつく
   • 回転前East: 回転後Northなら左1マス、Southなら右2マス
   • 回転前South: 左の壁にくっつく
   • 回転前West: 回転後Northなら右1マス、Southなら左2マス
4. 謎移動1(根っこに軸を置いて考えてみると非常にわかりやすい)
   • 回転前North: 一番左のブロックを固定し、(左|右)回転する位置に移動、例えばNorth->West(左回転)なら左1マス、上2マスの位置に移動するがこれは左端が固定されていると考えると直感的である。
   • 回転前East: 一番上のブロックを固定し、(左|右)回転する位置に移動
   • 回転前South: 一番右のブロックを固定し、(左|右)回転する位置に移動
   • 回転前West: 一番下のブロックを固定し、(左|右)回転する位置に移動
5. 謎移動2(4と反対の根っこで考える)
   • 回転前North: 一番右のブロックを固定し、(左|右)回転する位置に移動
   • 回転前East: 一番下のブロックを固定し、(左|右)回転する位置に移動
   • 回転前South: 一番左のブロックを固定し、(左|右)回転する位置に移動
   • 回転前West: 一番上のブロックを固定し、(左|右)回転する位置に移動

固定処理

単純に実装する場合はそこまで深く考えなければならない部分はないです。以下の流れで処理が行われるように書きましょう。

1. 本当に固定するべきか確かめる : 固定関数内で再度下方向移動不可か確認しましょう。呼び出し元のミスで空中に固定されてしまう...みたいなバグを回避できます。(今回自分もやらかしたバグ)
2. フィールドにブロックとして登録する(固定する)
3. ラインクリアを行う。得点をいれる。
4. 新しくテトリミノを降らせる。降らせる場所が埋まっていたらゲームオーバー

3、4については、例えばラインクリアにエフェクトを掛けたい時や、次のテトリミノが降ってくるまでにインターバルを置きたい場合などは、少し実装を工夫する必要が出てきます。これは解説が難しい部分なので、試行錯誤してみてください(例えばですが、落下中なのか、それともインターバル中なのかを表す列挙体をどこかに持たせる、などの方法が考えられます。)

ラインクリア(のうち行を詰める時)

自分も少し躓いてしまったポイントなので解説しておきます。

判定と消去は上下どちらの方向から行うか

少し考えてみるとわかりますが、対象行を発見するたびに消去を行うことにするならば、上下は無関係なことがわかります。最大4ライン消去することになり、それがご存知の通り「テトリス」です。

どこから移動を行うか

対象行を発見した際に上下どちらから移動を始めるかです。「上の行をそのままコピーしてくる」と考えます。つまり上の行に関して情報を残しておく必要があるので、対象行を含め 下から 移動を行っていくことになります。消去が完了したら一番上の行に空行を入れます。

描画処理とゴースト

方針としては、フィールドをコピーして、そのコピーに現在操作中のミノを投影し、それを描画用の配列として返せばよいです。

ここで関連事項としてゴーストについて解説します。ゴーストは案外簡単に取得できます。

1. 操作中ミノの現在座標を記憶しておく
2. ハードドロップみたいに降ろせなくなるまで下まで一気に下ろす
3. その時点での座標を記憶する
4. 操作中ミノをもとの場所に戻す

そして操作中ミノの取得&描画時についでに描画します。意外と簡単でしょう...?!

注意としては、実行してみればわかりますが、ゴーストの描写は操作中ミノの描写の前に行う必要があります。

ネクストの実装

テトリミノはランダムに降ってきますが、完全にランダムに降っているわけではありません(何言ってんだこいつ)

...要するにですね、例えばコイントスを思い浮かべてほしいのですが、完全にランダムなら 表が何度連続で出ても別に問題ありません。 (これは僕が大学で受けているプログラミング講義の教授の受け売りです)

テトリスで言えば 何度Iミノが連続で落ちてきてもそれはテトリスとして成り立つ ということです。なんかそういうテトリス見たことありますが、それは クソゲーです 。

これはちょっと極端に言い過ぎたかもしれないですけど、やってみればわかりますが完全にランダムに落ちてくるようにするとなかなか欲しいミノが来ないテトリスになり、難しく、あるいはつまらなく感じます。正直ホールドやゴーストなんかよりもずっと重要な要素です。

まぁ要は「全てのミノが確率とは別に均等に落ちてくる」ように実装する必要があります。ワールドルールでは、「7種類のミノ全てが落ちてくるまで同じミノがもう一度落ちてくることはない」ように実装しろと定められています。(解説サイト等ではよくこの7種類ごとのセットをツモと呼んだりします。)

例えば「T、O、L、T、Z、S、J、I、L、O、S、I、T、Z」みたいな並び方は不正⁸ですが、「T、L、Z、S、O、J、I、I、O、T、L、Z、S、J」は正しい配列です。ホールドまで含めるとIミノは最大でも3連続までしか不可能なので、テトリスも3連続が最大であることがわかります。

これの実装方法もいろいろ考えられますが、一例として「落とした個数を記憶する」という楽な実装方法があります。

Rust

struct MinoGenerator {
    dropped: Vec<(usize, u32)>,
    count  : u32,
    rng    : rand::rngs::ThreadRng,
}

impl MinoGenerator {
    fn new() -> MinoGenerator {
        let dropped = (0..7).map(|i| (i as usize, 0) ).collect();

        MinoGenerator {
            dropped,
            count  : 0,
            rng    : rand::thread_rng(),
        }
    }

    fn generate(&mut self) -> &'static Mino {
        if self.dropped.iter().all(|m| m.1 >= self.count) { self.count += 1 };
        let cands = self.dropped.iter().filter(|m| m.1 < self.count).collect::<Vec<_>>();
        let m = match cands.choose(&mut self.rng) {
            Some(v) => v,
            None    => panic!("Error in Mino Generating"),
        };
        let i: usize = m.0;
        self.dropped[i].1 += 1;
        [&I, &O, &S, &Z, &J, &L, &T][i]
    }
}

構造体 MinoGenerator には「それぞれのミノを何個落としたか、何ツモ目か、乱数生成器」を持たせています。

generate メソッドの

Rust

if self.dropped.iter().all(|m| m.1 >= self.count) { self.count += 1 };

この部分で、「すべてのミノの落とした回数がツモ数(何ツモ目)と一致したら、ツモ数をインクリメントする」という処理をし、

Rust

let cands = self.dropped.iter().filter(|m| m.1 < self.count).collect::<Vec<_>>();

この部分で「まだ落としていないミノの候補を絞る」ということを行っています。あとはこの候補から一つミノを選び、そのミノの落下数を増やしながらミノを返せばよいです。

ネクスト自体はキュー構造の動的配列(Rustだと VecDeque が使えます)に蓄えると補填・取り出し等が楽です。というかネクストってまさにキュー構造にうってつけな概念だと思います。

重力と遊び時間について

この項は筆者自身未だ納得の行っていない部分が多いです。ただし、重要な箇所なので説明を試みます

まず重力というのはテトリミノの落下速度のことを意味します。単位は「G」で、「1フレームあたりに何マス落ちるか」を表しています。例えば、「0.017G」ならば大体60フレーム(約1秒)で1段落ち、「1G」ならば1フレームで1段ずつ落ちます(操作不能なほど速い落下です。)

今回の実装方法では1G以上は考慮していませんが、この世には更に上の20Gとかいう化物もあります。20Gというのは「落下が始まった瞬間に接地している」という重力です。

もちろん、ゲームを面白くするにはラインが消去されるにつれ落下速度を上げるようにしたいです。そこで問題になってくるのが、「接地から何フレーム経ったら固定するか」です

落下が遅いうちは問題ないのですが、速くなってくるとこれは致命的な問題になってきます。先程出した20Gなどが良い例ですが、接地した瞬間に固定されてしまうようにすると「操作可能な要素が0になり」ます。確約されたゲームオーバーですね。

そのためにも、接地してからの数フレーム、あるいは数秒間は固定までに対して「遊び時間」を導入する必要性があります。

しかし遊び時間の導入を行うと、今度は「ハードドロップを知らない人」にとってフラストレーションの溜まるゲームとなります。接地してから何も操作を行ってない(本人としてはもうそこでいい)のに固定が行われないのは、確かにあまりよくありません。

となってくると、接地後に回転操作があったときにのみ、固定までの遊び時間を延長するような実装が思いつくかもしれません。

しかしその実装、ちょっとまってください！下手に導入すると「回転し続ければ永遠に固定されない」テトリスの完成です。せっかくの重力が台無しになる可能性すらあります。

という風に考えて行くと、つまるところ、次の3点を考慮しなければならないと結論付けられます。

• 接地後最低数フレームは固定しない
• 接地後操作がなければ固定、操作があれば遊び時間を入れる
• 遊び時間が一定値に達したら強制的に固定する

このあたりの感覚の調整はかなり難しいです。自然な感じに実装できたら素直にすごいと思います。

Rustでテトリスを作った感想とまとめ

本当はもう少し詳細に書くべき事項があったかもしれませんが、以上が自分がテトリスを作成する際に気を付けているポイントとなります。参考になったでしょうか？

Rustで書いてみましたが苦労もかなりありました。本当は1日か2日でテトリスを実装する予定だったのが、4日以上かかり、さらにFirebaseでデプロイするためにWebAssembly化するのに1週間かかり、執筆現在もうフラフラです()

というわけで、でもないですが触れてみた感想です。

良かった点

イテレータ周りは書いていて気持ちが良かったです。やはりPythonライクに書ける要素が多いのはPythonistaな自分にとっては嬉しかったです。またmatch式やif let式等、大抵の構文が式であるのは、可読性を大いに向上させている良い点だと改めて感じました。

苦労した点

なんだかんだ所有権周りをまだちゃんと理解しきれておらず、その辺りで苦労しました。Rustが難しいと言われる所以だと思います。

ただ、慣れな部分だとは思いますし、これでいいのかよくわからないですが コンパイルエラーの内容に従って修正したらあっさりと解決できました。

Rustのコンパイラってとにかく丁寧なんですよね、指摘された箇所についてちょちょいと直しただけで普通に動いたので、「よくわかっていないのにエラーを解決できた」というのを何回か経験してます。いいのかこれで...(良くない)

まとめ

人間苦労して習得したり苦労して得た物に愛着をもちがちですよね...Rustが好きになったように感じているのはただの吊橋効果？かもしれません。その疑いをもって、まだ勉強していない他の言語や他の概念にこれからも触れていければと思います。

Rustはイイぞ！(多分)...コメント、編集リクエスト、お待ちしております。ここまで読んでいただき、誠にありがとうございました。

1. この注釈をわざわざ見た人はまちカドまぞくをすこってくださいm(_ _)m ...で結局wasmってなんて読むんですかね？ ↩

2. ちなみに筆者はC++は書けません。C++にはガベージコレクションある...? ↩

3. https://github.com/o1810156/tetris_by_nim にありますが読めたもんじゃありませんねハイ。ちなみにある程度の学習には成功しました。ただ成果としては残念ながら微妙でした。 ↩

4. 今回は作成しませんでしたがRustでも動的ライブラリを作成する手段はあるようです。GCが働かないとは言っても、空間計算量(要はメモリ使用量)には気を配る必要はあるかもしれません。 ↩

5. ここ Option<&'static Mino> で良くないかですって...? それはそう(この場合列挙は Some(mino) と None )...いいじゃん！書きたかったんだもん！！！ ↩

6. Go言語に関しては全くやったことがないので間違った情報を載せている可能性があります(軽く調べた感じだと第一引数をレシーバとして受け取っているようです。根本の考え方に相違はなさそう)。あとPythonは微妙...?うるさい人には突っ込まれそうです。 ↩

7. 本当のテトリスでは最上部みたいなものはない可能性もあります。端の方で2マスぐらい上に飛び出していても、新しいテトリミノを降らせることができればゲームオーバーにならないという例があります。ぷよぷよなんかもそんな感じっぽい...? 商業レベルのテトリスを作成する場合は気にする必要があるかもしれませんが、難しそうなので筆者はやったことがないです。25行ぐらい取っておけばいける...? ↩

8. どうでもいいですけどなんかAtCoderのB問題かC問題で出てきそうな問題ですね ↩