1.はじめに
この記事は生存時間解析の1つ、Cox比例ハザードモデル(以下、Cox回帰)を実務で利用したい人に向けて作成しています。
主な内容としては、Cox回帰の基礎(2,3章)からやや発展的な内容(時間依存性Cox回帰(4章)、評価指標(5章)など)を扱います。
この記事を読むにあたって、特に必要な知識はありませんが、ロジスティック回帰などの初歩的な2値分類モデルの知識があると理解しやすいと思います。
2.生存時間解析の概要
Cox回帰は生存時間解析の手法の1つです。
ここではまず、Cox回帰の説明前により広い概念である生存時間解析の概要を説明します。
2-1.生存時間解析とは
生存時間解析とは、あるイベントが発生するまでの時間(生存時間) の推定を目的とした分析を指します。
ここで、イベントと生存時間は以下で定義されます。
- イベント:分析を行いたい重大な出来事(例:人の死亡)
- 生存時間:イベントが発生するまでの時間(例:人が死亡するまでの時間)
生存時間解析は、例のように「人が死亡するまでの時間」などの推定を目的として特に医療分野で利用されています。
また、医療分野に限らず、ビジネス分野でも生存時間解析を利用することができ、「機械の故障までの時間」や「顧客のサービス退会までの時間」の分析など幅広いシーンで利用することができます。
例えば、生存時間解析は下記のような疑問に答えることを目的に利用されます。
- 集団の平均的な生存時間はどの程度か
- 異なる集団(例:投薬有、投薬無etc.)の生存時間に差はあるか
- 現在の状態から予測される生存時間はどの程度か
1つ目の平均的な生存時間については単に生存時間の平均値を計算すればよいと思うかもしれません。しかし、実際には生存時間データ特有の「打ち切り」と呼ばれる状態が存在するため、単純な平均値で"平均的な生存時間"を計算することは困難です。
この打ち切りについて次節で説明します。
2-2.打ち切り
一般的な生存時間データには打ち切りと呼ばれる特徴的な状態があります。打ち切りは端的に言うと、「観測している間にイベントが発生しなかったデータ」です。
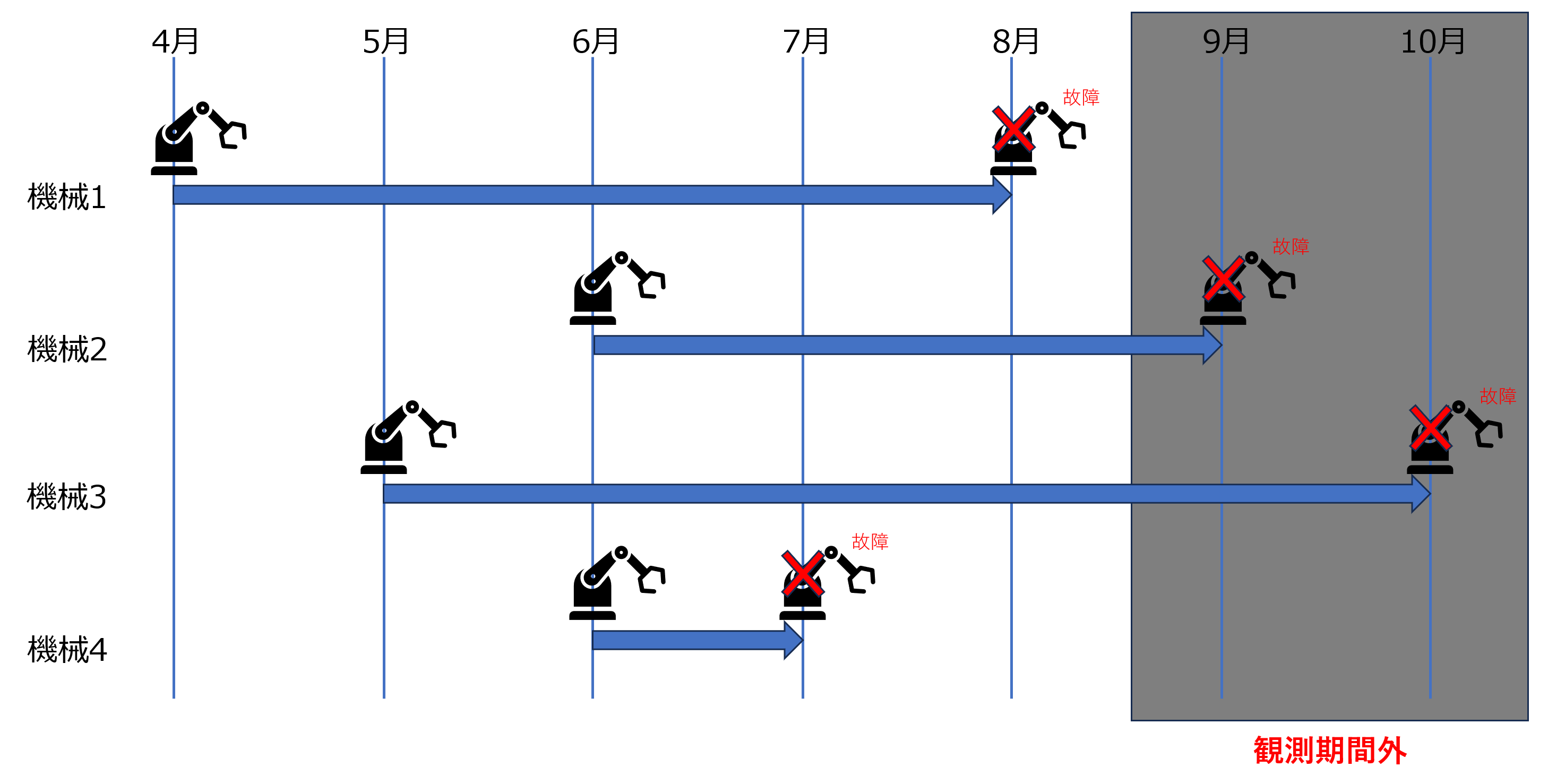
例として、機械の故障までの時間データを4-8月に取得し、以下のようなデータが取れたとします。
この時、9-10月は観測期間外のため、機械2と機械3は故障タイミングを取得できません。そのため、機械2(機械3)のデータは「2か月(3か月)以内では故障していない」という故障タイミングを特定できない不完全なデータになります。
このように「イベントが発生するまでの時間は不明だが、ある期間内でイベントが未発生であることは分かっている状況」を打ち切りと呼びます。
上の例では以下のように、機械2と機械3が打ち切りとなります。
このように観測期間などの影響で打ち切りデータが存在することが生存時間解析の特徴です。
打ち切りデータがある場合は、分析に注意が必要です。
例えば、上図のデータで平均的な故障時間(生存時間)を知りたい場合、打ち切りを気にせず、単純に平均値を計算すると
(4+{\color{red}2}+{\color{red}3}+1)/4=2.5か月,
となります。一方、上の例で9-10月も観測を続けて全ての故障を観測できた場合の正確な故障時間の平均値は
(4+{\mathbf 3}+{\mathbf 5}+1)/4=3.25か月,
と先ほどより少し大きな値になります。
つまり、打ち切りデータを含めて算出した故障時間(生存時間)は過小評価されてしまいます。
他に打ち切りデータを除外して平均値を計算するということも考えられますが、使用できるデータ数が減少するため、平均値の推定精度が悪化します。
そこで、生存時間解析では打ち切りデータを利用した上で、故障時間(生存時間)を過小評価しないように2-4節で紹介するKaplan-Meier法やCox回帰といった手法が用いられます。
2-3.ハザード関数
生存時間解析の手法に入る前に、ハザード関数について説明します。
この節の最後で説明するように、ハザード関数が分かれば様々な統計量を計算できるため、ハザード関数は生存時間解析において重要な役割を持ちます。
まず、経過時間$t$において以下のように記号を定義します。
\begin{align}
生存時間&:T, \\
[条件]を満たす確率&:P([条件]), \\
死亡関数&:F(t)=P(0\leq T\leq t), \\
死亡確率密度&:f(t)=\frac{d}{dt}F(t), \\
生存関数&:S(t)=P(T> t)=1-F(t).
\end{align}
この時、ハザード関数$h(t)$は生存関数$S(t)$を使って次のように定義されます。
S(t)=\exp\left(-\int_0^th(s)ds\right).
このハザード関数$h(t)$は死亡確率密度$f(t)$、生存関数$S(t)$で書けることが分かります(導出は下記の折りたたみ参照)。
\begin{align}
h(t)=\frac{f(t)}{S(t)}. \tag{1}
\end{align}
この式から分かるように、ハザード関数は「経過時間$t$まで生存している条件下で$t$に死亡する確率密度」と解釈することができます。
(1)式の導出(折りたたみ)
$S(t)$は$h(t),f(t)$を使って2通りで書くことができます。
\begin{align}
S(t)=&\exp\left(-\int_0^th(s)ds\right),\\
S(t)=&1-F(t)=1-\int_0^tf(s)ds.
\end{align}
それぞれの式を$t$で微分します。
\begin{align}
\frac{d}{dt}S(t)=&\frac{d}{dt}\exp\left(-\int_0^th(s)ds\right)\\
=&-h(t)\exp\left(-\int_0^th(s)ds\right)\\
=&-h(t)S(t),\\
\frac{d}{dt}S(t)=&\frac{d}{dt}\left(1-\int_0^tf(s)ds\right)\\
=&-f(t).
\end{align}
したがって、2式を比較して
h(t)=\frac{f(t)}{S(t)},
が得られます。
逆にハザード関数$h(t)$が分かれば、死亡確率密度$f(t)$を求めることができます。
f(t)=h(t)S(t)=h(t)\exp\left(-\int_0^th(s)ds\right).
死亡確率密度$f(t)$からは期待生存時間などの重要な統計量を計算できます。
そのため、ハザード関数$h(t)$は生存時間解析において非常に重要な関数となります。
このハザード関数の推定がCox回帰の目的になります。
2-4.生存時間解析の手法
ここでは生存時間解析で用いられる、関数推定方法や検定方法をいくつか簡単に紹介します。
Kaplan-Meier法
Kaplan-Meier法はある集団全体に対して生存関数$S(t)$を推定する方法です。
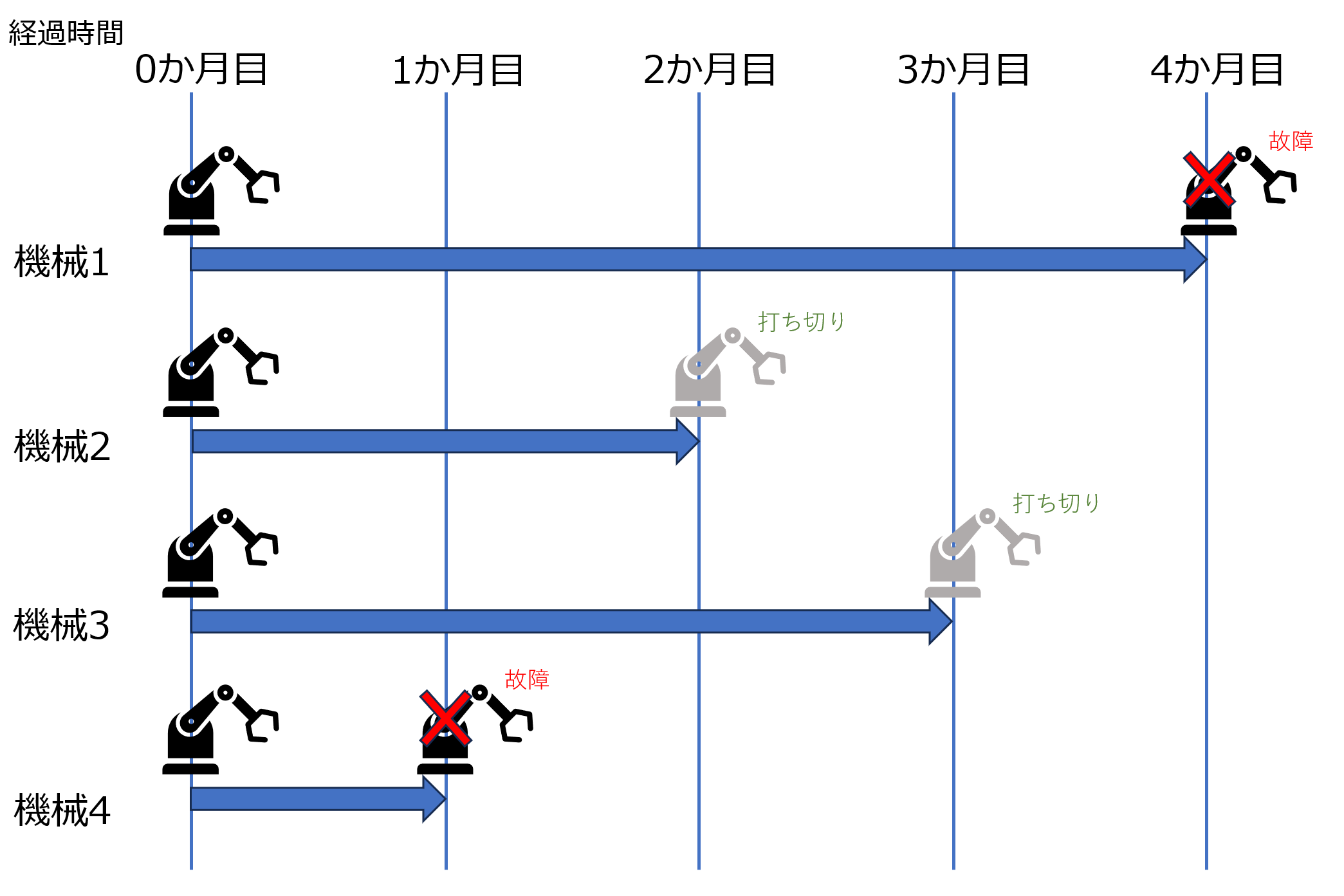
以下のように機械1~5がある場合を考えます。
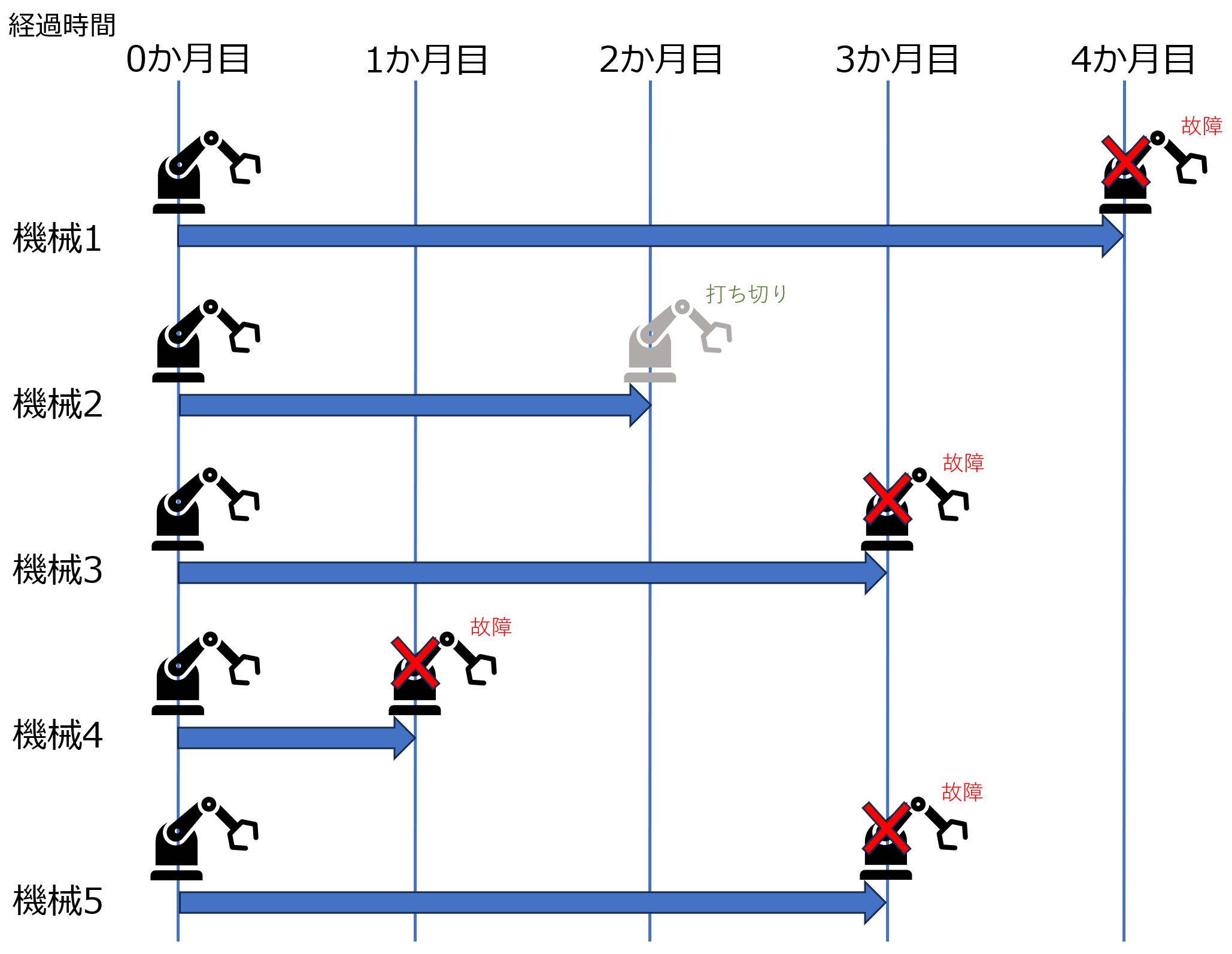
今、「$t$より前に故障していない条件の下で$t$にも故障しない確率:$\sigma(t)$」を故障が発生したタイミングそれぞれで求めます。
\begin{align}
\sigma(1か月目)=&\frac{4}{5}, \\
\sigma(3か月目)=&\frac{1}{3}, \\
\sigma(4か月目)=&0.
\end{align}
ここで打ち切り後のデータはカウントされなくなっていることに注意してください。例えば、$\sigma(3か月目)$の分母は3で機械1、機械3、機械5をカウントしていますが、打ち切り後の機械2はカウントしていません。(一方、$\sigma(1か月目)$では打ち切り前の機械2を含む機械1~5をカウントしています。)
この$\sigma(t)$をかけ合わせることで、生存関数$S(t)$を求めるのがKaplan-Meier法です。
\begin{align}
S(1か月)=&\frac{4}{5}, \\
S(3か月)=&\frac{4}{5}\times \frac{1}{3}=\frac{4}{15}, \\
S(4か月)=&\frac{4}{5}\times \frac{1}{3}\times 0=0.
\end{align}
ログランク検定
投薬有無、性別などの属性でデータを2つの集団に分割したとき、その2つの集団の生存時間が有意に異なるかを検定する手法の1つがログランク検定(log-rank test)です。
ログランク検定における帰無仮説は「比較する2つの集団の生存関数が等しい」です。この帰無仮説に対してp値を求めて帰無仮説が棄却されるかを調べます。帰無仮説が棄却された場合は2群の生存関数が有意に異なることが分かります。
詳細については"David W. Hosmer et al. 『生存時間解析入門』東京大学出版会"などを参照してください。
Cox比例ハザードモデル(Cox回帰)
Cox比例ハザードモデル(Cox回帰)はハザード関数の推定方法の1つです。
上で触れたKaplan-Meier法では属性情報(説明変数)によって全データをいくつかの集団に分割し、それぞれの集団に対して生存関数を推定、比較することが出来ました。
しかし、このようなデータの分割では対応が難しいケースがあります。
例えば、説明変数の種類が多い場合は集団の分割数が増えることで比較が難しくなります。また、説明変数が連続値で与えられる場合にはどこで集団を分割するかを決める必要があり、系統的な評価が難しくなります。
このような困難を解決する方法として、データを分割せずに回帰によってハザード関数を推定することが考えられます。このハザード関数の回帰を行うのがCox比例ハザードモデル(Cox回帰)です。
本記事の残りの部分ではこのCox回帰について説明を行います。
3. Cox比例ハザードモデル(Cox回帰)
生存時間解析の手法の1つ、Cox比例ハザードモデル(以下、Cox回帰)について説明します。
ただし、簡単のためこの章では説明変数$X=(X_1,X_2,\cdots,X_N)$が時間依存しない場合を考えます(時間に依存した時間依存性Cox回帰については次章で説明します)。
3-1. Cox回帰とは
前章で言及したようにCox回帰ではハザード関数$h(t)$の推定を行います。
Cox回帰では次のようにハザード関数$h(t)$の形を仮定します。
経過時間$t$、説明変数$\boldsymbol{X}=(X_1,X_2,\cdots,X_N)$におけるハザード関数:
\begin{align}
h(t,X)=&h_0(t)\exp\left(\boldsymbol{\beta X}\right)\\
=&h_0(t)\exp(\beta_1X_1+\beta_2X_2+\cdots+\beta_NX_N),
\end{align}
ここで、$h_0(t)$:基準ハザード関数、$\boldsymbol{\beta}=(\beta_1,\cdots,\beta_N)$:回帰係数で$(\boldsymbol{\beta X}=\sum_{i=1}^N\beta_iX_i=\beta_1X_1+\beta_2X_2+\cdots+\beta_NX_N)$と略記しています。
基準ハザード関数$h_0(t)$は経過時間$t$のみの関数で、具体的な関数系は指定しません。そのため、ハザード関数$h(t,X)$の関数系はCox回帰において部分的にしか仮定されていません。(このように、部分的にしか関数系が決まっていないモデルはセミパラメトリックモデルと呼ばれます。)
比例ハザード性
Cox回帰の重要な性質はハザード関数$h(t,X)$同士の比が説明変数$X$のみに依存しているということです。
実際、説明変数の異なる2つのハザード関数$h(t,X),h(t,X')$の比を計算すると、$h_0(t)$が消えて$X,X'$だけの関数になります。
\begin{align}
\frac{h(t,X)}{h(t,X')}=&\frac{h_0(t)\exp(\boldsymbol{\beta X})}{h_0(t)\exp(\boldsymbol{\beta X}')}\\
=&\frac{\exp(\boldsymbol{\beta X})}{\exp(\boldsymbol{\beta X}')}.
\end{align}
特に、$X,X'$が時間依存しない場合には、ハザード関数の比が時間依存しなくなります。
このようなハザード関数の比が時間依存しない性質を比例ハザード性と呼びます。比例ハザード性は非常に強い仮定であるため、Cox回帰を利用する際は比例ハザード性を仮定する妥当性があるか注意する必要があります。
3-2. 部分尤度
Cox回帰では部分尤度と呼ばれる尤度関数によって回帰係数$\beta_1,\cdots,\beta_N$を決定します。"部分"尤度と呼ばれるのは、基準ハザード関数$h_0(t)$を含まない$\beta_1,\cdots,\beta_N$だけで決まる尤度であるためです。
この節では部分尤度の導出を直感的な方法で説明します。
(より詳細な議論については4章末【Breslow法による部分尤度・基準ハザード関数】に記載していますので、興味があればそちらをご覧ください。)
2つの故障データに対する部分尤度
まず、簡単のために次のような2つの故障データに対する部分尤度を考えます。
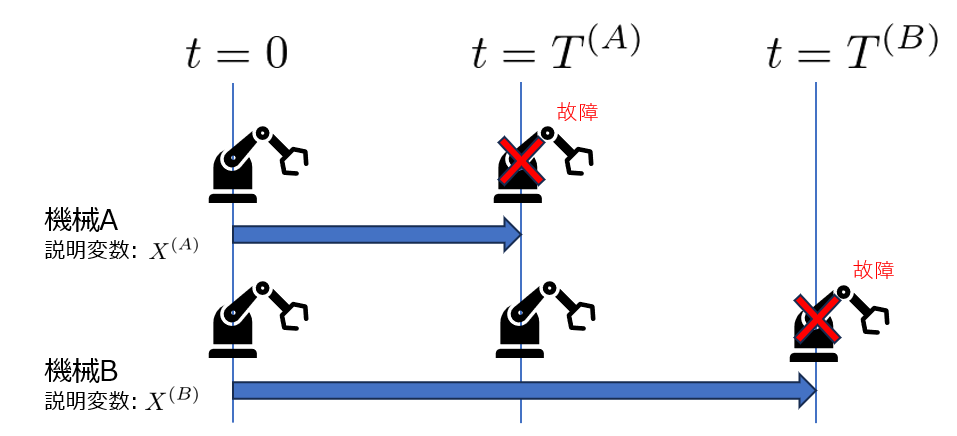
$A,B$の各関数は以下のように上付き添え字$(A),(B)$をつけて定義します。
\begin{align}
A,Bの死亡(故障)確率密度&:f^{(A)}(t),f^{(B)}(t), \\
A,Bの生存確率&:S^{(A)}(t),S^{(B)}(t).
\end{align}
この時、時間$t=T^{(A)}$に実現している状態は「Aが故障、Bは生存(未故障)」です。このような状況が実現するもっともらしさ(尤度)を考えます。
この尤度は「$A,B$のどちらか一方が経過時間$T^{(A)}$に故障したことが分かっている条件の下、$A$が故障していた確率:$l^{(A)}(\beta;T^{(A)})$」によって求めることができます。
\begin{align}
l^{(A)}(\beta;T^{(A)})=&\frac{f^{(A)}(T^{(A)})S^{(B)}(T^{(A)})}{f^{(A)}(T^{(A)})S^{(B)}(T^{(A)})+S^{(A)}(T^{(A)})f^{(B)}(T^{(A)})}\\
=&\frac{h(T^{(A)},X^{(A)})}{h(T^{(A)},X^{(A)})+h(T^{(A)},X^{(B)})},
\end{align}
上記の式変形では$h(t,X^{(i)})=\frac{f^{(i)}(t)}{S^{(i)}(t)}$を使っています。
さらに、Cox回帰のハザード関数
\begin{align}
h(t,X)=&h_0(t)\exp(\boldsymbol{\beta X})\\
=&h_0(t)\exp(\beta_1X_1(t)+\beta_2X_2(t)+\cdots+\beta_NX_N(t)),
\end{align}
を代入すると基準ハザード関数$h_0(t)$に依らない式が得られます。
\begin{align}
l^{(A)}(\beta;T^{(A)})=&\frac{h_0(T^{(A)})\exp(\boldsymbol{\beta X}^{(A)})}{h_0(T^{(A)})\exp(\boldsymbol{\beta X}^{(A)})+h_0(T^{(A)})\exp(\boldsymbol{\beta X}^{(B)})}\\
=&\frac{\exp(\boldsymbol{\beta X}^{(A)})}{\exp(\boldsymbol{\beta X}^{(A)})+\exp(\boldsymbol{\beta X}^{(B)})}.
\end{align}
次に$t=T^{(B)}$の故障タイミングを考えます。このタイミングでは「Bが故障」が発生しています。
この時の尤度$l^{(B)}(\beta;T^{(B)})$を同様に求めます。
\begin{align}
l^{(B)}(\beta;T^{(B)})=&\frac{f^{(B)}(T^{(B)})}{f^{(B)}(T^{(B)})}\\
=&\frac{h(T^{(B)},X^{(B)})}{h(T^{(B)},X^{(B)})}\\
=&\frac{\exp(\boldsymbol{\beta X}^{(B)})}{\exp(\boldsymbol{\beta X}^{(B)})}
\end{align}
全ての時間に渡った尤度$L(\beta)$は各故障時間の尤度の積で導出できます。
\begin{align}
L(\beta)=&l^{(A)}(\beta;T^{(A)})\times l^{(B)}(\beta;T^{(B)})\\
=&\frac{\exp(\boldsymbol{\beta X}^{(A)})}{\exp(\boldsymbol{\beta X}^{(A)})+\exp(\boldsymbol{\beta X}^{(B)})}\times\frac{\exp(\boldsymbol{\beta X}^{(B)})}{\exp(\boldsymbol{\beta X}^{(B)})}.
\end{align}
この$L(\beta)$が2つの故障データ$A,B$に対する部分尤度となります。
打ち切りがある場合の部分尤度
次に、打ち切りがある場合の部分尤度を求めます。
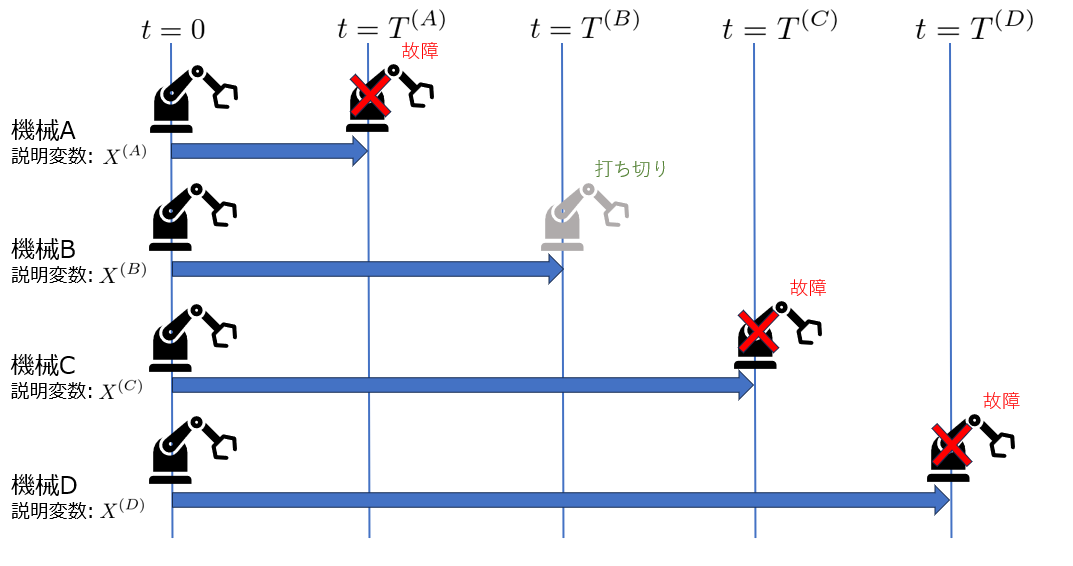
以下のような4つの機械がある場合を考えます。
この時の部分尤度を導出する手順は、上で説明した機械$A,B$だけのケースと同様に行うことができます。
(1)各故障タイミングでの尤度$l^{(i)}(\beta;T^{(i)})$を導出。
(2)$l^{(i)}(\beta;T^{(i)})$の積から部分尤度$L(\beta)$を導出。
ここで、$i=A,B,C,D$です。ただし、打ち切りデータ(機械$B$)には故障タイミングがないことに注意が必要です。
(1)各故障タイミングでの尤度$l^{(i)}(\beta;T^{(i)})$を導出。
まず、各故障タイミングでの尤度を求めます。
今回の場合は$T^{(A)},T^{(C)},T^{(D)}$が故障タイミングのため、各時間での尤度は以下のようになります。(以下、$\boldsymbol{\beta X}^{(i)}=\beta_1X_1^{(i)}+\cdots+\beta_NX_N^{(i)}$と略記しています。)
\begin{align}
l^{(A)}(\beta;T^{(A)})=&\frac{\exp(\boldsymbol{\beta X}^{(A)})}{\exp(\boldsymbol{\beta X}^{(A)})+\exp(\boldsymbol{\beta X}^{(B)})+\exp(\boldsymbol{\beta X}^{(C)})+\exp(\boldsymbol{\beta X}^{(D)})}, \\
l^{(C)}(\beta;T^{(C)})=&\frac{\exp(\boldsymbol{\beta X}^{(C)})}{\exp(\boldsymbol{\beta X}^{(C)})+\exp(\boldsymbol{\beta X}^{(D)})}, \\
l^{(D)}(\beta;T^{(D)})=&\frac{\exp(\boldsymbol{\beta X}^{(D)})}{\exp(\boldsymbol{\beta X}^{(D)})}.
\end{align}
打ち切りデータ(機械$B$)が分母にのみ現れていることに注意してください。分子に現れない理由は、打ち切りデータに故障タイミングがないためです。
一方で分母については、故障、打ち切りに関係なくそのタイミングまでに故障していないデータが使用されます。例えば、$l^{(A)}(\beta;T^{(A)})$では打ち切りデータ(機械$B$)、故障データ(機械$A,C,D$)のどちらも$t=T^{(A)}$までに故障していない機械として分母に現れます。
部分尤度$L(\beta)$は各故障タイミングでの尤度の積で与えられます。
\begin{align}
L(\beta)=&l^{(A)}(\beta;T^{(A)})\times l^{(C)}(\beta;T^{(C)})\times l^{(D)}(\beta;T^{(D)})\\
=&\frac{\exp(\boldsymbol{\beta X}^{(A)})}{\exp(\boldsymbol{\beta X}^{(A)})+\exp(\boldsymbol{\beta X}^{(B)})+\exp(\boldsymbol{\beta X}^{(C)})+\exp(\boldsymbol{\beta X}^{(D)})}\\
&\times\frac{\exp(\boldsymbol{\beta X}^{(C)})}{\exp(\boldsymbol{\beta X}^{(C)})+\exp(\boldsymbol{\beta X}^{(D)})}\\
&\times \frac{\exp(\boldsymbol{\beta X}^{(D)})}{\exp(\boldsymbol{\beta X}^{(D)})}.
\end{align}
機械数がさらに増えても同じように計算できます。任意の機械数に対する部分尤度$L(\beta)$は以下の形になります。
L(\beta)=\prod_{i\in \mathcal{A}} \frac{\exp(\boldsymbol{\beta X}^{(i)})}{\sum_{j\in \Lambda_i}\exp(\boldsymbol{\beta X}^{(j)})}=\prod_{i\in \mathcal{A}} \frac{\exp(\beta_1 X_1^{(i)}+\cdots+\beta_NX_N^{(i)})}{\sum_{j\in \Lambda_i}\exp(\beta_1 X_1^{(j)}+\cdots+\beta_NX_N^{(j)})}.
ただし、$\mathcal{A},\Lambda_i$は以下を表します。
\begin{align}
\mathcal{A}:&故障(打ち切りでない)データ全体の集合\\
\Lambda_i:&T^{(i)}以後(T^{(i)}含む)に故障、打ち切りになるデータの集合
\end{align}
タイデータ
ここまでの説明は暗に同時間で故障が発生しないことを仮定していました。
同時間で故障が発生したデータをタイデータと呼び、タイデータが存在する場合は部分尤度$L(\beta)$が変更されます。タイデータがある場合の部分尤度の計算方法には厳密な値を与えるExact法の他に近似手法であるBreslow法、Efron法などが存在します。
特にBreslow法では、タイデータがあったとしても同じ計算方法で部分尤度を導出できます。(Exact法、Efron法については"大橋靖雄 et al. 『生存時間解析』東京大学出版会"などを参照してください。)
タイデータがある場合の部分尤度(Breslow法):
L(\beta)=\prod_{i\in \mathcal{A}} \frac{\exp(\beta_1 X_1^{(i)}+\cdots+\beta_NX_N^{(i)})}{\sum_{j\in \Lambda_i}\exp(\beta_1 X_1^{(j)}+\cdots+\beta_NX_N^{(j)})}.
Breslow法はタイデータがあまり多くないとき、良い近似になります。計算時間が短いこと、歴史的に早期に提案されたことから多くのパッケージで利用されています。
部分尤度まとめ
以上より、説明変数$X^{(i)}$が時間依存しない場合の尤度は部分尤度:
L(\beta)=\prod_{i\in \mathcal{A}} \frac{\exp(\beta_1 X_1^{(i)}+\cdots+\beta_NX_N^{(i)})}{\sum_{j\in \Lambda_i}\exp(\beta_1 X_1^{(j)}+\cdots+\beta_NX_N^{(j)})},
によって与えられます。この部分尤度$L(\beta)$を最大化する$(\beta_1,\cdots,\beta_N)$がCox回帰で採用されます。
部分尤度の重要な特徴は基準ハザード関数$h_0(t)$に依存しないことです。そのため、Cox回帰では基準ハザード関数$h_0(t)$を特定せずに回帰係数$\beta$を決定することができます。特に、説明変数による影響度(ハザード比)を調べる場合は基準ハザード関数が必要ないため、基準ハザード関数を特定せずに回帰係数を決定できることは非常に有用な性質となります。
ただし、ビジネス的な用途でCox回帰を使用する場合は説明変数の影響度だけでなく期待生存時間などを予測したい場合が多いです。その際は、基準ハザード関数を含むハザード関数全体を推定する必要があります。
そこで、次節では基準ハザード関数を推定する方法を紹介します。
3-3. 基準ハザード関数の推定
ここまでで、Cox回帰の回帰係数$\beta$を部分尤度$L(\beta)$で求め、各説明変数の影響度を測ることができるようになりました。しかし、ビジネス的な用途では機械が故障するまでの時間などを知りたいケースが多く、基準ハザード関数を推定してハザード関数全体を知る必要があります。
この節では基準ハザード関数を推定する方法の1つであるBreslow法を紹介します。
なお、このBreslow法は前節で紹介したタイデータがある場合の近似手法と同じものです。Breslow法ではハザード関数を近似しており、その結果として「タイデータのある部分尤度」と「基準ハザード関数」を求めることができます。(詳細は4章末【Breslow法による部分尤度・基準ハザード関数の導出】をご覧ください。)
Breslow法では基準ハザード関数を階段関数で近似します。
$\alpha={0,1,2,\cdots}$として$t_\alpha$で等間隔に時間を分割します($\Delta t=t_{\alpha+1}-t_\alpha,t_0=0$)。
(必ずしも等間隔である必要はありませんが、ここでは簡単のため等間隔で分割します)
この時、基準ハザード関数は以下のように階段関数で近似されます。
h_0(t)=\frac{d_\alpha}{\Delta t\sum_{j\in \lambda_\alpha}\exp(\beta_1X_1^{(j)}+\cdots+\beta_NX_N^{(j)})},~~(t_{\alpha-1}<t\leq t_\alpha),
ここで、$d_\alpha,\lambda_\alpha$は次で定義されます。
\begin{align}
d_\alpha:&t_\alpha に故障した機械の数\\
\lambda_\alpha:&t_\alpha 以後(t_\alpha 含む)に故障、打ち切りになる機械の集合
\end{align}
このような式で基準ハザード関数を推定できる理由は4章末の【Breslow法による部分尤度・基準ハザード関数の導出】で説明していますので興味があればご覧ください。
4. 時間依存性Cox回帰
ここまで、説明変数$X$が時間依存しない場合を考えていました。
この章では、少し発展的な内容として時間依存がある説明変数$X(t)$の取り扱いについて説明します。
4-1. 時間依存性Cox回帰とは
説明変数$X$に時間依存性のある場合のCox回帰を特に時間依存性Cox回帰と呼びます。
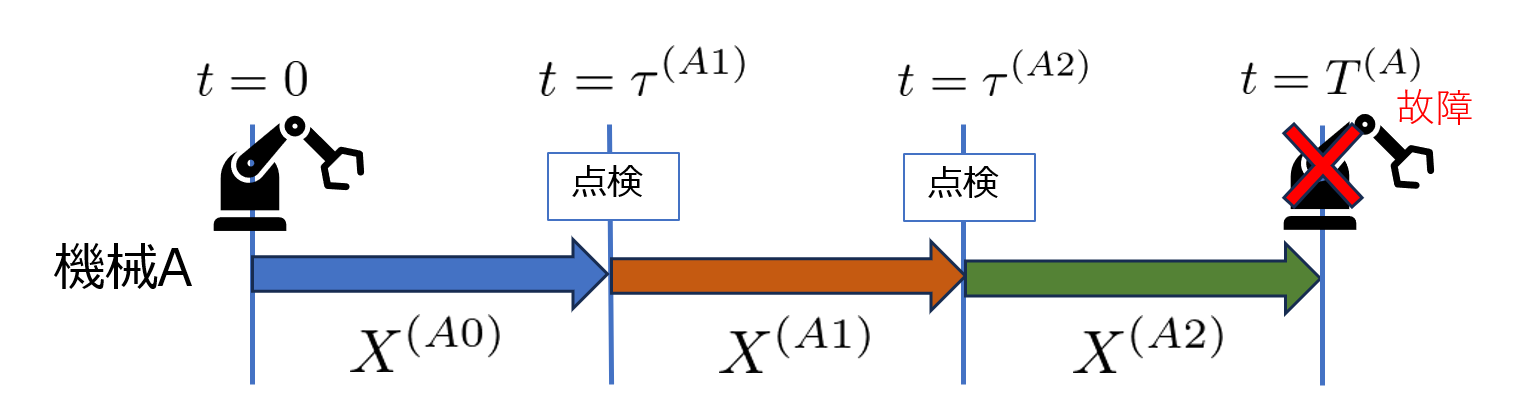
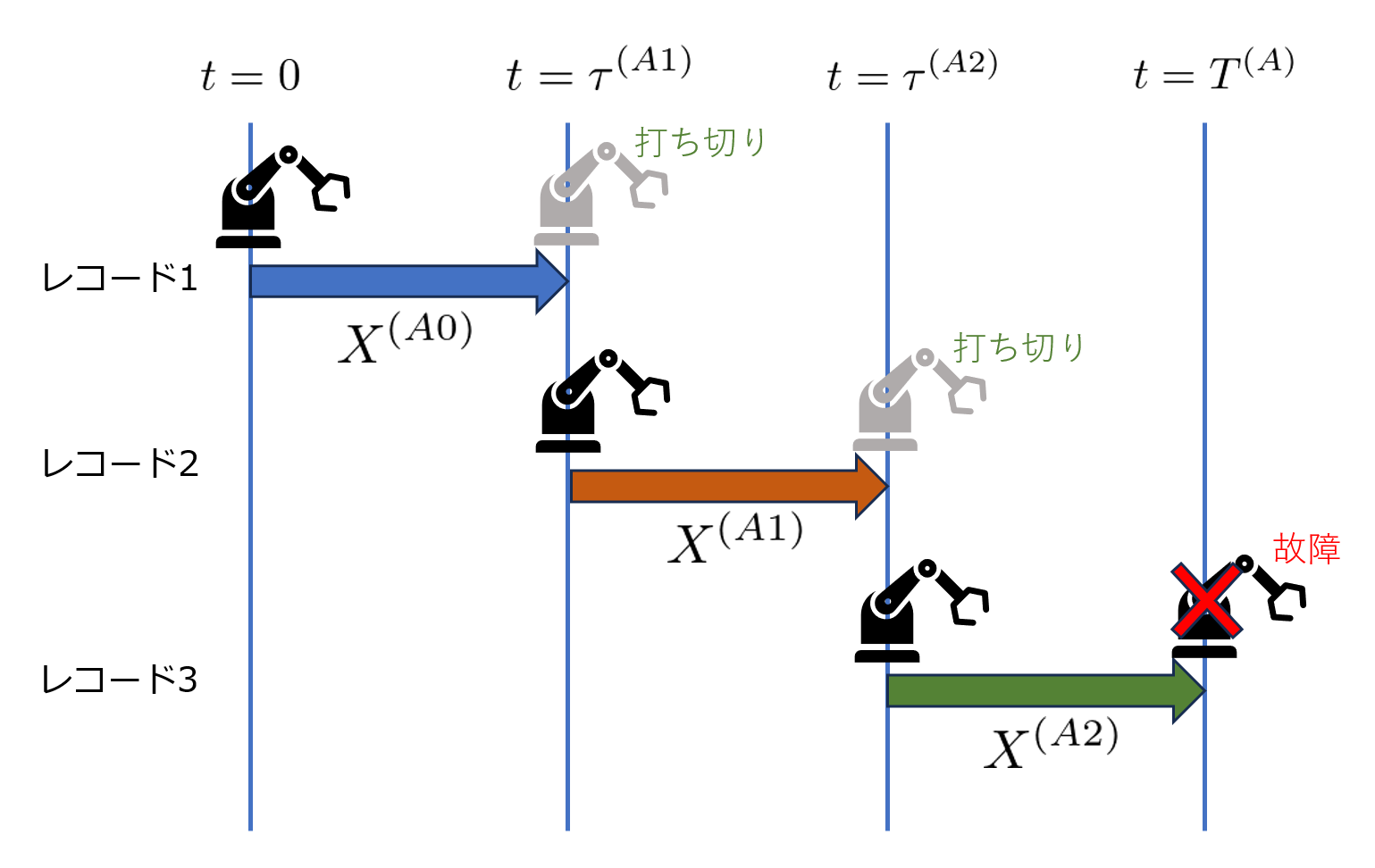
例えば、以下のように点検によって説明変数$X$が更新される状況を考えます。
この場合、1回目の点検が行われるまでの期間$0\sim\tau^{(A1)}$における説明変数は最初の測定値$X^{(A0)}$ですが、次の期間$\tau^{(A1)}\sim\tau^{(A2)}$では$X^{(A1)}$に変わります。
このように説明変数が時間経過によって変化する場合に拡張したCox回帰が時間依存性Cox回帰です。
4-2. データ作成方法
説明変数に時間依存性がある場合、説明変数が更新されるごとに新しいレコードとしてデータを作成します。(同じレコードにデータを追加していく方法もありますが、カラム数が更新のたびに増えてしまう欠点があるため、ここでは触れません。)
例えば、前節のイラストの機械$A$のデータは以下のように点検タイミングで分割して別のレコードとして保存します。
| レコード | 機械 | 開始時間 | 終了時間 | (終了時間での)故障有無 | 説明変数 |
|---|---|---|---|---|---|
| 1 | A | 0 | $\tau^{(A1)}$ | 0 | $X^{(A0)}$ |
| 2 | A | $\tau^{(A1)}$ | $\tau^{(A2)}$ | 0 | $X^{(A1)}$ |
| 3 | A | $\tau^{(A2)}$ | $T^{(A)}$ | 1 | $X^{(A2)}$ |
各レコードにはどの期間のデータか分かるように開始時間、終了時間を記録します。そして、終了時間においてイベントが発生したかのフラグを立てます。
この例では、終了時間で故障が発生した最後のレコード3に故障有無のフラグを立てます。一方、レコード1,2は終了時間では未故障のため、データ上は打ち切りと同様に扱われます。
4-3. ハザード関数
時間依存性Cox回帰のハザード関数の形は時間依存のない場合と同じ形を仮定します。
説明変数に時間依存がある場合のハザード関数:
\begin{align}
h(t,X(t))=&h_0(t)\exp(\boldsymbol{\beta X}(t))\\
=&h_0(t)\exp(\beta_1X_1(t)+\beta_2X_2(t)+\cdots+\beta_NX_N(t)).
\end{align}
時間依存のない場合と同様に、説明変数の異なる2つのハザード関数$h(t,X(t)),h(t,X'(t))$の比を取ると$h_0(t)$が消えて$X,X'$だけの関数になります。
\begin{align}
\frac{h(t,X(t))}{h(t,X'(t))}=&\frac{h_0(t)\exp(\boldsymbol{\beta X}(t))}{h_0(t)\exp(\boldsymbol{\beta X}'(t))}\\
=&\frac{\exp(\boldsymbol{\beta X}(t))}{\exp(\boldsymbol{\beta X}'(t))}.
\end{align}
このように、時間依存性がある場合でもハザード比は同じ形になります。
ただし、$X(t),X'(t)$が時間依存するため、このハザード関数の比も一般に時間変化します。そのため、時間依存性Cox回帰では一般に比例ハザード性は成立しません。
4-4. 部分尤度
部分尤度の議論は説明変数の時間依存有無でほとんど変わりません。
唯一の変更点は、どの時間の説明変数$X(t)$を使って計算するかに注意することです。
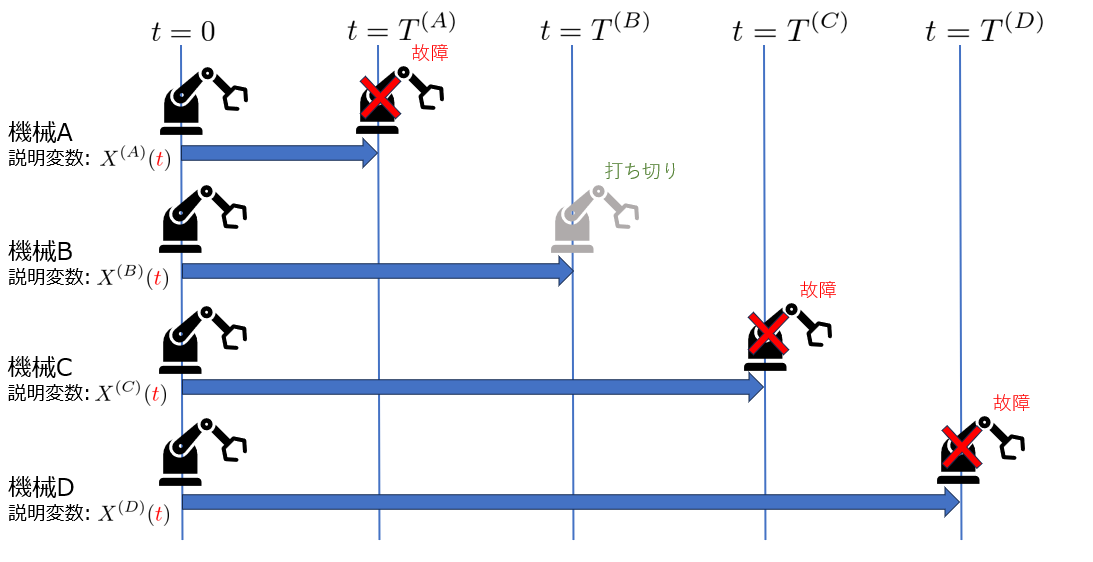
以下のような4つの機械データがある場合を考えます。
この設定は時間依存のない場合の尤度を説明した際の設定に説明変数の時間依存性を加えたものです$(X\rightarrow X({\color{red}t}))$。
まず、各故障タイミングでの尤度を求めます。
この例では$T^{(A)},T^{(C)},T^{(D)}$が故障タイミングのため、各時間での尤度は以下のようになります。
\begin{align}
l^{(A)}(\beta;T^{(A)})
=&\frac{\exp(\boldsymbol{\beta X}^{(A)}(T^{(A)}))}{\exp(\boldsymbol{\beta X}^{(A)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(B)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(C)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(D)}(T^{(A)}))}, \\
l^{(C)}(\beta;T^{(C)})=&\frac{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))}{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))+\exp(\boldsymbol{\beta X}^{(D)}(T^{(C)}))}, \\
l^{(D)}(\beta;T^{(D)})=&\frac{\exp(\boldsymbol{\beta X}^{(D)}(T^{(D)}))}{\exp(\boldsymbol{\beta X}^{(D)}(T^{(D)}))}.
\end{align}
ここで重要なことは各時間の尤度$l^{(A)}(\beta;T^{(A)}),l^{(C)}(\beta;T^{(C)}),l^{(D)}(\beta;T^{(D)})$の式中で、説明変数の時間が各故障タイミング $T^{(A)},T^{(C)},T^{(D)}$にそろっていることです。
例えば、$l^{(C)}(\beta;T^{(C)})$が「$T^{(C)}$において、$C,D$のどちらか1つが故障した条件の下で$C$が故障する確率」であることを思い出せば、以下のように時間がそろうことを確認できます。
\begin{align}
l^{(C)}(\beta;T^{(C)})=&\frac{f^{(C)}(T^{(C)})S^{(D)}(T^{(C)})}{f^{(C)}(T^{(C)})S^{(D)}(T^{(C)})+S^{(C)}(T^{(C)})f^{(D)}(T^{(C)})}\\
=&\frac{h(T^{(C)},X^{(C)}(T^{(C)}))}{h(T^{(C)},X^{(C)}(T^{(C)}))+h(T^{(C)},X^{(D)}(T^{(C)}))}\\
=&\frac{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))}{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))+\exp(\boldsymbol{\beta X}^{(D)}(T^{(C)}))}.
\end{align}
部分尤度$L(\beta)$は各時間の尤度の積で求めることができます。
\begin{align}
L(\beta)=&l^{(A)}(\beta;T^{(A)})\times l^{(C)}(\beta;T^{(C)})\times l^{(D)}(\beta;T^{(D)})\\
=&\frac{\exp(\boldsymbol{\beta X}^{(A)}(T^{(A)}))}{\exp(\boldsymbol{\beta X}^{(A)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(B)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(C)}(T^{(A)}))+\exp(\boldsymbol{\beta X}^{(D)}(T^{(A)}))}\\
&\times \frac{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))}{\exp(\boldsymbol{\beta X}^{(C)}(T^{(C)}))+\exp(\boldsymbol{\beta X}^{(D)}(T^{(C)}))}\\
&\times\frac{\exp(\boldsymbol{\beta X}^{(D)}(T^{(D)}))}{\exp(\boldsymbol{\beta X}^{(D)}(T^{(D)}))}.
\end{align}
このように説明変数の時間に注意することを除けば、時間依存性Cox回帰においても部分尤度の形は変わりません。
一般の場合の時間依存性Cox回帰の部分尤度は以下で与えられます。
\begin{align}
L(\beta)=&\prod_{i\in \mathcal{A}} \frac{\exp(\boldsymbol{\beta X}^{(i)}(T^{(i)}))}{\sum_{j\in \Lambda_i}\exp(\boldsymbol{\beta X}^{(j)}(T^{(i)}))}\\
=&\prod_{i\in \mathcal{A}} \frac{\exp(\beta_1 X_1^{(i)}(T^{(i)})+\cdots+\beta_NX_N^{(i)}(T^{(i)}))}{\sum_{j\in \Lambda_i}\exp(\beta_1 X_1^{(j)}(T^{(i)})+\cdots+\beta_NX_N^{(j)}(T^{(i)}))},
\end{align}
ここで、$\mathcal{A},\Lambda_i$の定義は時間依存性がない場合と同じです。
\begin{align}
\mathcal{A}:&故障(打ち切りでない)データ全体の集合\\
\Lambda_i:&T^{(i)}以後(T^{(i)}含む)に故障、打ち切りになるデータの集合
\end{align}
タイデータ
タイデータ(同時刻の故障、打ち切り)がある場合の取り扱いは時間依存がない場合と変わらず、Breslow法では部分尤度に変更は必要ありません。
L(\beta)=\prod_{i\in \mathcal{A}} \frac{\exp(\beta_1 X_1^{(i)}(T^{(i)})+\cdots+\beta_NX_N^{(i)}(T^{(i)}))}{\sum_{j\in \Lambda_i}\exp(\beta_1 X_1^{(j)}(T^{(i)})+\cdots+\beta_NX_N^{(j)}.(T^{(i)}))}
例として、次のような機械の故障データに対して部分尤度を計算してみます。
| 機械ID | 開始時間 | 終了時間 | (終了時間での)故障有無 | 説明変数 | |
|---|---|---|---|---|---|
| $X_1$ | $\cdots$ | 1 | 0 | 10 | 0 | 9 | $\cdots$ |
| 1 | 10 | 27 | 1 | 16 | $\cdots$ |
| 2 | 0 | 13 | 0 | 15 | $\cdots$ |
| 2 | 13 | 42 | 0 | 19 | $\cdots$ |
| 2 | 42 | 50 | 0 | 23 | $\cdots$ |
| 3 | 0 | 21 | 0 | 17 | $\cdots$ |
| 3 | 21 | 45 | 1 | 20 | $\cdots$ |
部分尤度の計算結果は次のようになります。
\begin{align}
L(\beta)=&l(t=27,\beta)\times l(t=45,\beta)\\
=&\frac{\exp(16\beta_1+\cdots)}{\exp(16\beta_1+\cdots)+\exp(19\beta_1+\cdots)+\exp(20\beta_1+\cdots)}\\
&\times \frac{\exp(20\beta_1+\cdots)}{\exp(20\beta_1+\cdots)+\exp(23\beta_1+\cdots)}.
\end{align}
4-5. 基準ハザード関数の推定
基準ハザード関数の推定も時間依存性がない場合と同様にBreslow法で行うことができます。
$\alpha={0,1,2,\cdots}$として$t_\alpha$で時間を分割します。($\Delta t=t_{\alpha+1}-t_\alpha, t_0=0$)
この時、基準ハザード関数は以下で近似されます。
h_0(t)=\frac{d_\alpha}{\Delta t\sum_{j\in \lambda_\alpha}\exp(\beta_1X_1^{(j)}(t_\alpha)+\cdots+\beta_NX_N^{(j)}(t_\alpha))},~~(t_{\alpha-1}<t\leq t_\alpha),
ここで、$d_\alpha,\lambda_\alpha$は時間依存性のない場合と同じ定義です。
\begin{align}
d_\alpha:&t_\alpha に故障した機械の数\\
\lambda_\alpha:&t_\alpha 以後(t_\alpha 含む)に故障、打ち切りになる機械の集合
\end{align}
【Breslow法による部分尤度・基準ハザード関数の導出】
ここではより詳細な議論としてBreslow法における部分尤度の導出を説明します。
上で行った部分尤度の導出では、
「1つの機械が故障した条件の下で特定の機械が故障している確率」
によって尤度が算出できることを前提にしていました。しかし、この前提は「1つの機械が故障した条件の下で」という条件付けが必要な理由が明確ではありません。ここでの議論ではこのような条件付けをせずにより自然な議論で尤度を導入します。
まず、$i=1,2,\cdots,M$の$M$個のデータに対して以下のように記号を定義します。
\begin{align}
説明変数:&X^{(i)}(t)=(X_1^{(i)}(t),\cdots,X_N^{(i)}(t)), \\
故障\ \mathrm{or}\ 打ち切りデータのフラグ:&\Delta_i(1:故障、0:打ち切り), \\
故障時間\ \mathrm{or}\ 打ち切り時間:&T^{(i)}.
\end{align}
説明変数$X$、時間$t$における関数を次のように定義します。
\begin{align}
ハザード関数:h(X,t)&=h_0(t)\exp(\boldsymbol{\beta X}(t))\\
&=h_0(t)\exp(\beta_1 X_1(t)+\cdots+\beta_N X_N(t)), \\
生存関数:S(X,t)&=\exp\left(-\int_0^th(X(s),s)ds\right), \\
死亡(故障)確率密度:f(X,t).&
\end{align}
この時、実際に観測された$X^{(i)}(t),\Delta_i,T^{(i)}(i=1,\cdots,M)$が実現する尤度$\mathcal{L}$は以下のように書くことができます。
\begin{align}
\mathcal{L}=\prod_{i=1}^Mf(X^{(i)}(T^{(i)}),T^{(i)})^{\Delta_i}S(X^{(i)}(T^{(i)}),T^{(i)})^{1-\Delta_i}.
\end{align}
この式は$\Delta_i$の値によって$S(X,t),f(X,t)$を使い分けるようになっています。
- $\Delta_i=1$:$T^{(i)}$で故障しているため、その瞬間の故障確率密度$f(X^{(i)}(T^{(i)}),T^{(i)})$を利用
- $\Delta_i=0$:$T^{(i)}$で打ち切りしているため、$T^{(i)}$までの生存確率$S(X^{(i)}(T^{(i)}),T^{(i)})$を利用
それでは、尤度$\mathcal{L}$を計算していきます。
\begin{align}
\mathcal{L}=&\prod_{i=1}^Mf(X^{(i)}(T^{(i)}),T^{(i)})^{\Delta_i}S(X^{(i)}(T^{(i)}),T^{(i)})^{1-\Delta_i}\\
=&\prod_{i=1}^M\left(\frac{f(X^{(i)}(T^{(i)}),T^{(i)})}{S(X^{(i)}(T^{(i)}),T^{(i)})}\right)^{\Delta_i}S(X^{(i)}(T^{(i)}),T^{(i)})\\
=&\prod_{i=1}^Mh(X^{(i)}(T^{(i)}))^{\Delta_i}S(X^{(i)}(T^{(i)}),T^{(i)})\\
=&\prod_{i=1}^Mh_0(T^{(i)})^{\Delta_i}\exp(\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)}))
\exp\left(-\int_0^{T^{(i)}}h_0(s)\exp(\boldsymbol{\beta X}^{(i)}(s))ds\right).
\end{align}
さらに計算を進めるために、Breslow法における近似を行います。
Breslow法では階段関数によって関数を近似します。
\begin{align}
h_0(t)=&h_{0\alpha},\ (t_{\alpha-1}<t\leq t_\alpha), \\
X^{(i)}(t)=&X^{(i)\alpha},\ (t_{\alpha-1}<t\leq t_\alpha),
\end{align}
ここで、$t_\alpha,(\alpha=0,1,2,\cdots)$は経過時刻を細かく分割したもので、以下で定義します。
\begin{align}
\Delta t &= t_\alpha-t_{\alpha-1} (\mathrm{const}), \\
t_0=&0.
\end{align}
また、記号を以下で新たに定義します。
\begin{align}
d_\alpha:&t_\alpha に故障した機械の数\\
\gamma(\ ):&T=t_{\gamma(T)}\\
\lambda_\alpha:&t_\alpha 以後(t_\alpha 含む)に故障、打ち切りになる機械の集合
\end{align}
これらの近似と記号を用いて尤度$\mathcal{L}$を計算していきます。
\begin{align}
\prod_{i=1}^Mh_0(T^{(i)})^{\Delta_i}=&\prod_{\alpha=0}^\infty (h_{0\alpha})^{d_\alpha}=\prod_{\alpha=1}^\infty (h_{0\alpha})^{d_\alpha},\\
\prod_{i=1}^M\exp\left(-\int_0^{T^{(i)}}h_0(s)\exp(\boldsymbol{\beta X}^{(i)}(s))ds\right)=&\prod_{i=1}^M\exp\left(-\sum_{\alpha=1}^{\gamma(T^{(i)})}h_{0\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right)\\
=&\prod_{i=1}^M\prod_{\alpha=1}^{\gamma(T^{(i)})}\exp\left(-h_{0\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right)\\
=&\prod_{\alpha=1}^{\infty}\prod_{i\in\lambda_\alpha}\exp\left(-h_{0\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right)\\
=&\prod_{\alpha=1}^{\infty}\exp\left(-h_{0\alpha}\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right).
\end{align}
これらを代入して、尤度$\mathcal{L}$を得ます。
\begin{align}
\mathcal{L}=&\left(\prod_{\alpha=1}^\infty (h_{0\alpha})^{d_\alpha}\right)\left(\prod_{i=1}^M\exp(\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)}))\right)
\prod_{\alpha=1}^{\infty}\exp\left(-h_{0\alpha}\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right).
\end{align}
対数尤度$\log \mathcal{L}$は以下で与えられます。
\begin{align}
\log\mathcal{L}=&\sum_{\alpha=1}^\infty d_\alpha\log h_{0\alpha}+\sum_{i=1}^M\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)})-
\sum_{\alpha=1}^{\infty}h_{0\alpha}\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t.
\end{align}
この対数尤度$\log\mathcal{L}$を最大化する$h_{0\alpha},\beta$を求めることがCox回帰の目的です。
まず、$\beta$を固定して$h_{0\alpha}$で微分します。
\begin{align}
\frac{\partial}{\partial h_{0\alpha}}\log\mathcal{L}=&\frac{d_\alpha}{h_{0\alpha}}-\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t.
\end{align}
(1)$d_\alpha=0$のとき
\begin{align}
\frac{\partial}{\partial h_{0\alpha}}\log\mathcal{L}=&-\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\leq 0.
\end{align}
ハザード関数が0以上であることから$h_{0\alpha}\geq 0$ですので、$h_{0\alpha}=0$で$\log\mathcal{L}$が最大になります。
(2)$d_\alpha\neq0$のとき
\begin{align}
\frac{\partial}{\partial h_{0\alpha}}\log\mathcal{L}=0\Rightarrow h_{0\alpha}=\frac{d_\alpha}{\Delta t\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})}.
\end{align}
したがって、対数尤度$\log\mathcal{L}$を最大化する$h_{0\alpha}$は次で与えられます。
h_{0\alpha}=
\begin{cases}
0 & (d_\alpha=0) \\
\frac{d_\alpha}{\Delta t\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})} & (d_\alpha\neq. 0)
\end{cases}.
この$h_{0\alpha}$を尤度$\mathcal{L}$に代入して、$\beta$だけの尤度を得ます。
\begin{align}
\mathcal{L}=&\left(\prod_{\alpha=1}^\infty \left(\frac{d_\alpha}{\Delta t\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})}\right)^{d_\alpha}\right)\left(\prod_{i=1}^M\exp(\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)}))\right)\\
&\times\prod_{\alpha=1}^{\infty}\exp\left(-\frac{d_\alpha}{\Delta t\sum_{j\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(j)\alpha})}\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})\Delta t\right)\\
=&\left(\prod_{\alpha=1}^\infty \left(\frac{1}{\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})}\right)^{d_\alpha}\right)\left(\prod_{\alpha=1}^\infty \left(\frac{d_\alpha}{\Delta t}\right)^{d_\alpha}\right)\left(\prod_{i=1}^M\exp(\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)}))\right)\\
&\times\prod_{\alpha=1}^{\infty}\exp\left(-d_\alpha\right)\\
=&\left(\prod_{\alpha=1}^\infty \left(\frac{d_\alpha}{\Delta t}\right)^{d_\alpha}\exp(-d_\alpha)\right)\left(\prod_{j=1}^M \left(\frac{1}{\sum_{i\in\Lambda_j}\exp(\boldsymbol{\beta X}^{(i)}(T^{(j)}))}\right)^{\Delta_j}\right)\prod_{i=1}^M\exp(\Delta_i\boldsymbol{\beta X}^{(i)}(T^{(i)}))\\
=&\left(\prod_{\alpha=1}^\infty \left(\frac{d_\alpha}{\Delta t}\right)^{d_\alpha}\exp(-d_\alpha)\right)\prod_{i\in\mathcal{A}}^M \frac{\exp(\boldsymbol{\beta X}^{(i)}(T^{(i)}))}{\sum_{j\in\Lambda_i}\exp(\boldsymbol{\beta X}^{(j)}(T^{(i)}))}.
\end{align}
定数係数を取り除くと$\beta$だけに対する部分尤度$L(\beta)$が得られます。
\begin{align}
L(\beta)=&\prod_{i\in\mathcal{A}}^M \frac{\exp(\boldsymbol{\beta X}^{(i)}(T^{(i)}))}{\sum_{j\in\Lambda_i}\exp(\boldsymbol{\beta X}^{(j)}(T^{(i)}))}.
\end{align}
以上がBreslow法における部分尤度の導出です。また、基準ハザード関数は以下で与えられます。
h_0(t)=
\begin{cases}
0 & (t_{\alpha-1}<t\leq t_\alpha,\ d_\alpha=0) \\
\frac{d_\alpha}{\Delta t\sum_{i\in\lambda_\alpha}\exp(\boldsymbol{\beta X}^{(i)\alpha})} & (t_{\alpha-1}<t\leq t_\alpha,\ d_\alpha\neq 0)
\end{cases}.
5. モデルの評価指標
ここまでで、Cox回帰モデルをどのように作成するかについて説明してきました。しかし、実際にモデルをビジネスに生かす際はモデルの精度評価が必要不可欠です。
この章では作成したCox回帰モデルの精度をどのように評価するかについて説明します。
5-1. 時点AUC
時点AUCとはある特定の経過時間$T$において死亡(故障)、生存(未故障)の2値分類の精度を評価する指標です。
例えば、30日後の故障確率に興味があるときは、「予測スコア:30日の死亡(故障)確率」、「30日での実際の死亡(故障)の有無」を比較して通常の二値分類と同様にAUCを算出します。
5-2. C-index
C-indexはConcordance indexやC統計量とも呼ばれる評価指標です。
C-indexの表すものは予測$T^{(i)}_{pred}$と実測$T^{(i)}$を比較した際に生存時間の大小関係がどの程度一致しているかです。C-indexは$[0,1]$の値を取り、大小関係が完全に一致している場合には$1$、完全に不一致の場合には$0$となります。
まず、タイデータがない($i\neq j \Rightarrow T^{(i)}\neq T^{(j)}$)場合のC-index $C$は次で定義されます。
C = \frac{\sum_{i\neq j}\Delta_iI(T^{(i)}<T^{(j)})[I(T_{pred}^{(i)}<T_{pred}^{(j)})+0.5I(T_{pred}^{(i)}=T_{pred}^{(j)})]}{\sum_{i\neq j}\Delta_iI(T^{(i)}<T^{(j)})},
ここで、指示変数$\Delta_i$、指示関数$I([条件])$は次で定義されます。
\begin{align}
\Delta_i &=
\begin{cases}
1 & (イベント発生)\\
0 & (打ち切り)
\end{cases}, &
I([条件]) &=
\begin{cases}
1 & ([条件]が真)\\
0 & ([条件]が偽)
\end{cases}.
\end{align}
タイデータがある場合のC-indexはやや複雑になります。
C=\frac{1}{2}\left(\frac{\sum_{i\neq j}\mathrm{sgn}(T_{pred}^{(i)},T_{pred}^{(j)})\mathrm{csgn}(T^{(i)},\Delta_i,T^{(j)},\Delta_j)}{\sum_{i\neq j}[\mathrm{csgn}(T^{(i)},\Delta_i,T^{(j)},\Delta_j)]^2}+1\right),
ここで、新たに定義した指示関数$\mathrm{sgn}(\ ),\mathrm{csgn}(\ )$は以下で定義します。
\begin{align}
\mathrm{sgn}(T_{pred}^{(i)},T_{pred}^{(j)})=&I(T_{pred}^{(i)}\geq T_{pred}^{(j)})-I(T_{pred}^{(i)}\leq T_{pred}^{(j)}),\\
\mathrm{csgn}(T^{(i)},\Delta_i,T^{(j)},\Delta_j)=&\Delta_jI(T^{(i)}\geq T^{(j)})-\Delta_iI(T^{(i)}\leq T^{(j)}).
\end{align}
説明変数に時間依存がある場合
説明変数に時間依存がある場合でもC-indexを定義することができます。
例えば、タイデータがない場合は以下で与えられます。
C = \frac{\sum_{i\neq j}\Delta_iI(T^{(i)}<T^{(j)})[I(\boldsymbol{\beta X}^{(i)}(T^{(i)})>\boldsymbol{\beta X}^{(j)}(T^{(i)}))+0.5I(\boldsymbol{\beta X}^{(i)}(T^{(i)})=\boldsymbol{\beta X}^{(j)}(T^{(i)}))]}{\sum_{i\neq j}\Delta_iI(T^{(i)}<T^{(j)})}.
この式は、時間依存性がない場合には上で与えたタイデータがない場合のC-indexに帰着します。(説明変数に時間依存性がなければ、$T_{pred}^{(i)}\lesseqgtr T_{pred}^{(j)}\iff \boldsymbol{\beta X}^{(i)}\gtreqless \boldsymbol{\beta X}^{(j)}$(複号同順)が成立するためです。)
詳細についてはWalter K. Kremers, 2007をご覧ください。
5-3. 評価指標の使い分け
Cox回帰の評価指標には時点AUCとC-indexの2つが存在することを述べました。この2つの評価指標はモデルの使用目的によって使い分けます。
時点AUCとC-indexのメリット、デメリットをまとめると以下のようになります。
| 評価指標 | メリット | デメリット |
|---|---|---|
| 時点AUC | 特定の経過時間における識別性能を評価できる | 時点ごとにAUCが算出されるため、全時間に渡った統一的な評価が難しい |
| C-index | モデルに対して1つの値のみが算出され、時系列に渡った統一的な評価ができる | 特定の時点における精度評価ができない |
このように、評価指標ごとに評価することができる項目が異なるため、モデルの目的に沿った評価指標を選択して使うことになります。
大まかな使い分けは以下のようになります。
- 時点AUC:特定の時点の精度が重要な場合(例: 特定の時間経過後の生存確率)
- C-index:時間全体に渡った精度が重要な場合(例: 生存時間の期待値)
6. Pythonの実装例
最後にPythonのlifelinesパッケージによるCox回帰の実装例を簡単に紹介します。
lifelinesは生存時間解析のパッケージで、Cox回帰の他に2-4節で紹介したKaplan-Meier法やログランク検定なども実行することができます。
実行環境は以下の通りです。
- Python (ver 3.9.7)
- lifelines (ver 0.27.7)
説明変数に時間依存がない場合
(1) サンプルデータのロード
#受刑者の釈放後の追跡データ(イベント:釈放後の逮捕)
data = lifelines.datasets.load_rossi()
(2) モデルの作成
#ライブラリのロード
from lifelines import CoxPHFitter
#モデルのインスタンス化
cph = CoxPHFitter()
#モデルのフィッティング
cph.fit(data #学習データ
,duration_col = 'week' #イベント、打ち切りまでの期間のカラム
,event_col = 'arrest' #イベント発生フラグのカラム
)
(3) 結果のサマリー表示
#モデル結果サマリー表示
cph.print_summary()
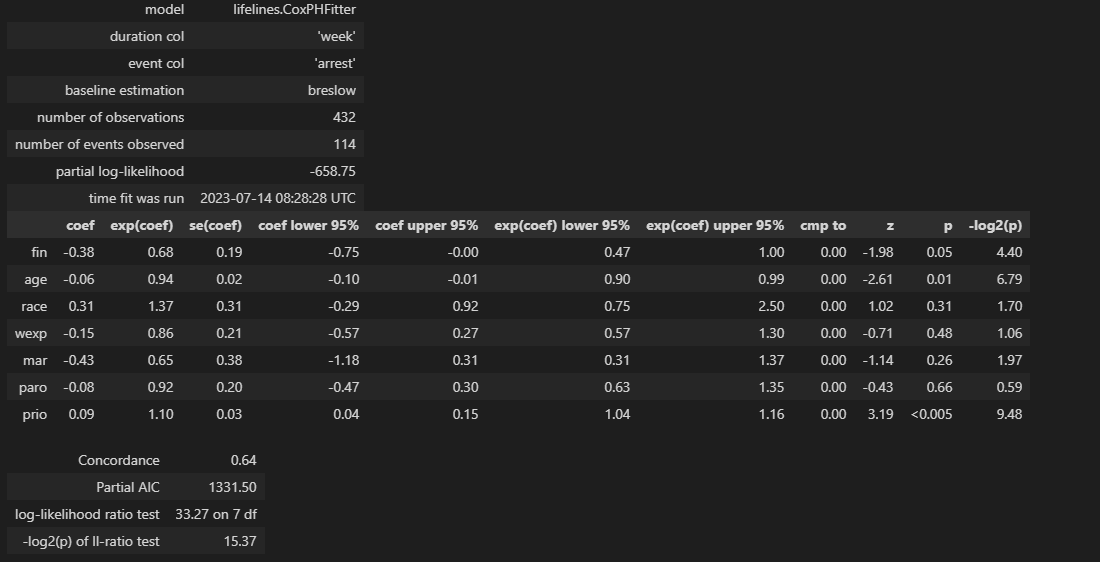
実行結果
説明変数ごとに回帰係数(coef)が出力されます。
説明変数の生存時間への影響度が有意かはp値(p)を確認してください。ここには帰無仮説「回帰係数が0」に対するp値が表示されています。
モデルの精度についてはConcordance、Partial AICなどが表示されます。
Concordanceは5-2節で紹介したC-indexのことです。1に近いほど精度が良いことを表します。Partial AICは部分尤度を利用したAIC(赤池情報量基準)です。こちらは値が小さいほど汎化性能が高いモデルと評価できます。
説明変数に時間依存がある場合
(1) サンプルデータのロード
#患者さんの生存時間データ
data = lifelines.datasets.load_stanford_heart_transplants()
(2) モデルの作成
#ライブラリのロード
from lifelines import CoxTimeVaryingFitter
#モデルのインスタンス化
ctv = CoxTimeVaryingFitter()
#モデルのフィッティング
ctv.fit(data3
,id_col='id'
,event_col='event'
,start_col='start'
,stop_col='stop'
)
(3) 結果のサマリー表示
#モデル結果サマリー表示
ctv.print_summary()
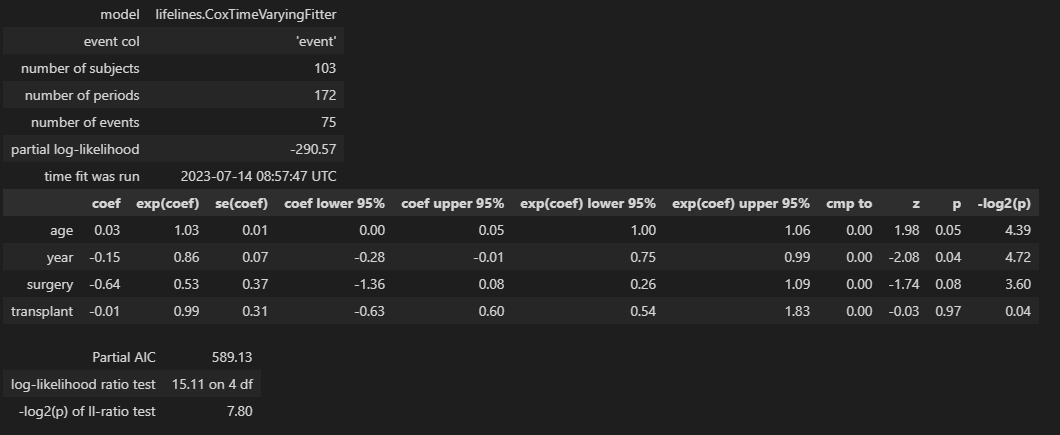
時間依存性Cox回帰の場合のサマリーも説明変数については同様です。
説明変数ごとに回帰係数(coef)、p値(p)が表示されます。
時間依存の場合、Concordanceについてはlifelinesで表示できません。
(Partial AICは部分尤度を利用したAIC(赤池情報量基準)です。こちらは値が小さいほど汎化性能が高いモデルと評価できます。)
7. おわりに
この記事では生存時間解析の基礎からCox回帰のやや発展的な内容(時間依存性Cox回帰、評価指標)までをまとめました。
Cox回帰を使ってみたい方のお役に立てれば幸いです。