1. はじめに
データ分析業務において、最近は機械学習や統計学だけでなく、数理最適化にも注目が集まっているように感じています。そこで本記事では、数理最適化とはどのようなものか、基本的な事項についてご紹介します。
2. 数理最適化の基礎
2-1. 数理最適化とは
数理最適化とは、解決したい問題を数式で表し、問題に対する最適な解を求めるための方法論です。数理最適化を活用できる問題は身近にも数多く存在します。例えば、
- 1日に必要な栄養素が取れる食品をできるだけ安く買いたい
- A駅からC駅までB駅を経由して最も早く到着したい
などは、数理最適化の枠組みでアプローチすることができます。ビジネスシーンで言えば、ぱっと思いつくものだけでも
- 従業員の出勤の頻度や時間帯が均等になるようにシフトを組みたい
- 利益を最大化するための商品の生産量を決定したい
があります。昨今の計算機の性能向上と汎用ソルバーの進歩により、簡単なプログラミングだけで数理最適化を試せるようになってきています。それに伴い、ビジネスにおける課題解決に数理最適化を活用できる可能性が広がっています。予測精度の高い機械学習技術と組み合わせることで、予測結果をもとにビジネス上の最適な意思決定をするといった活用方法もあり、数理最適化の重要度は今後一段と高まると考えています。
2-2. 数理最適化問題の定式化
数理最適化では、解決したい問題の目的と条件を数式で表します(これを定式化と呼びます)。例えば、売上を最大化するように商品A, Bの生産量を求めたいという問題は、
- 目的
- 売上(=商品Aの単価$\times$商品Aの生産数+商品Bの単価$\times$商品Bの生産数)の最大化
- 条件
- 商品A, Bの生産に使用する材料の量は在庫量以下とする
- 商品A, Bの生産量は0以上とする
と整理することができます。
これを数式で表してみます。商品A, Bの生産量を $x_{A}, x_{B}$、商品A, Bの単価を $p_{A}, p_{B}$、商品A, Bを1単位生産するのに必要な材料の量を $c_{A}, c_{B}$、材料の在庫量を $s$とすると、解決したい問題は
${\rm maximize}\quad p_{A}x_{A} + p_{B}x_{B}$
${\rm subject\ to}\quad c_{A}x_{A} + c_{B}x_{B} \leq s $
$\quad \quad \quad \quad \quad \ x_{A} \geq 0$
$\quad \quad \quad \quad \quad \ x_{B} \geq 0$
という形で書き下すことができます。ここで、${\rm maximize}$は最大化を表し、${\rm subject\ to}$は条件の始まりを表します。
また、数理最適化問題を解くことで値を決める変数(ここでは $x_{A}, x_{B}$)を決定変数、最適化の対象となる数式(ここでは $p_{A}x_{A} + p_{B}x_{B}$)を目的関数、満たすべき条件を表す数式(ここでは${\rm subject\ to}$以降の3つの式)は制約条件と呼ばれます。ここでは、売上は多い方が望ましいため目的を最大化としていますが、コストなど少ない方が望ましい場合は、目的を最小化(${\rm minimize}$)にすることもできます。
2-3. 数理最適化問題の分類
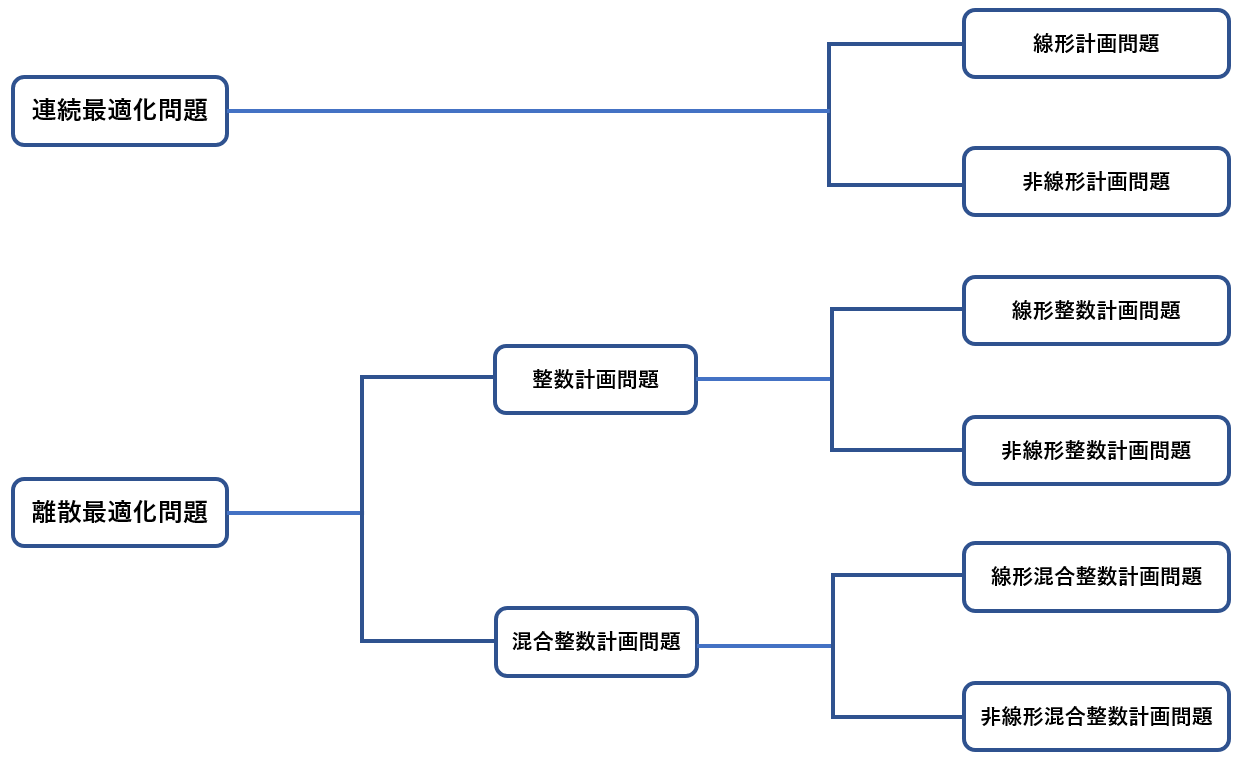
数理最適化問題は、決定変数が連続値か離散値か、目的関数と制約条件(を表す等式や不等式)が線形か非線形か、の観点で分類されます。数理最適化問題の分類を図1にまとめました。
変数が連続値の場合は連続最適化問題 (continuous optimization problem)、離散値の場合は離散最適化問題 (discrete optimization problem)と呼ばれ1、一般に離散最適化の方が解くのが難しくなります。また、目的関数と制約条件がともに線形関数で表される線形計画問題 (LP: linear programming problem) と、非線形関数で表された目的関数や制約条件を含む非線形計画問題 (NLP: nonlinear programming problem) に分類されます。
離散最適化問題の中で、決定変数が整数値のみをとる問題を整数計画問題 (IP: integer programming problem)、一部の決定変数が整数値をとり、残りの決定変数は実数をとる問題を混合整数計画問題 (MIP: mixed integer programming problem) と呼びます。
以降では、数理最適化問題の中でも、整数計画問題の解法についてご紹介します。その他の数理最適化問題の解法については他の書籍や記事に譲りますが、例えば線形計画問題については、単体法や内点法と呼ばれる効率の良い解法が開発されています。これらの解法にご興味ある方は参考文献2などをご覧ください。
3. 整数計画問題の解法
整数計画問題の解法は、制約条件を満たすものの中で最良の解を求める厳密解法と、必ずしも最適ではないが良い解を求める近似解法に大別されます。厳密解法には、決まったタイプの数理最適化問題にのみ適用できる典型解法(専用解法)と、あらゆる問題に適用できる汎用解法があります。汎用解法は、基本的には計算時間がかかっても最適解を求める解法であり、数理最適化ソルバーにも実装されています。近似解法は、厳密に最適な解が求まる保証はありませんが、計算時間が比較的短い、数理最適化ソルバーを使わずに実装可能、などのメリットがあります。
それぞれの解法のメリット・デメリットを以下の表にまとめました。こちらはあくまで相対的な評価です。どの解法を採用するかは、解に要求される精度や、許容できる計算時間などを加味して決める必要があります。
| 汎用性 | 厳密性 | 計算時間 | |
|---|---|---|---|
| 典型解法 | × | 〇 | 〇 |
| 汎用解法 | 〇 | 〇 | × |
| 近似解法 | 〇 | × | 〇 |
次に代表的な厳密解法、近似解法をいくつかご紹介します。
3-1. 厳密解法
3-1-1. 分枝カット法
整数計画問題の代表的な厳密解法として、分枝限定法 (branch-and-bound method) と切除平面法 (cutting plane method) が知られています。さらに、分枝限定法に切除平面法を組み合わせた分枝カット法 (branch-and-cut method) は、数理最適化ソルバーの求解方針のベースとなっています。決定変数が0か1の2値をとる場合、考慮(探索)すべき解の候補の数は$2^n$個($n$は変数の数)と膨大な数になり、決定変数が整数値(0, 1, 2, ...)をとる場合は、解の候補の数はさらに増えます。分枝カット法は、最適である見込みのない解の探索を省略することで、効率的な解の探索を実現しています。
まず、分枝限定法について説明します。分枝限定法は、直接解くことが難しい問題を小規模な問題に分割する分枝操作と、分割された問題の中から最適解が得られる見込みのない問題を見つける限定操作を繰り返し適用する手法です。分枝限定法は、整数計画問題以外にも多くの数理最適化問題で使用されます。以降では、目的関数を最大化する問題を解くことを想定して説明します。
分枝限定法は、解の下界と上界と呼ばれる概念を使って、解の最適性を失わず無駄な探索を省略します。下界とは、最適値(最適解における目的関数の評価値)より小さい(もしくは等しい)ことが保証された値です。上界とは、最適値より大きい(もしくは等しい)ことが保証された値で、各決定変数の整数条件を実数条件に緩和した線形計画緩和問題を解いて求めることが多いです。つまり、目的関数を $f(\boldsymbol{x})$、整数計画問題の最適解を $\boldsymbol{x}^*$、線形計画緩和問題の最適解を $\boldsymbol{\bar{x}}$ とすると、
f(\boldsymbol{\bar{x}}) \geq f(\boldsymbol{x}^*)
が成り立ちます。
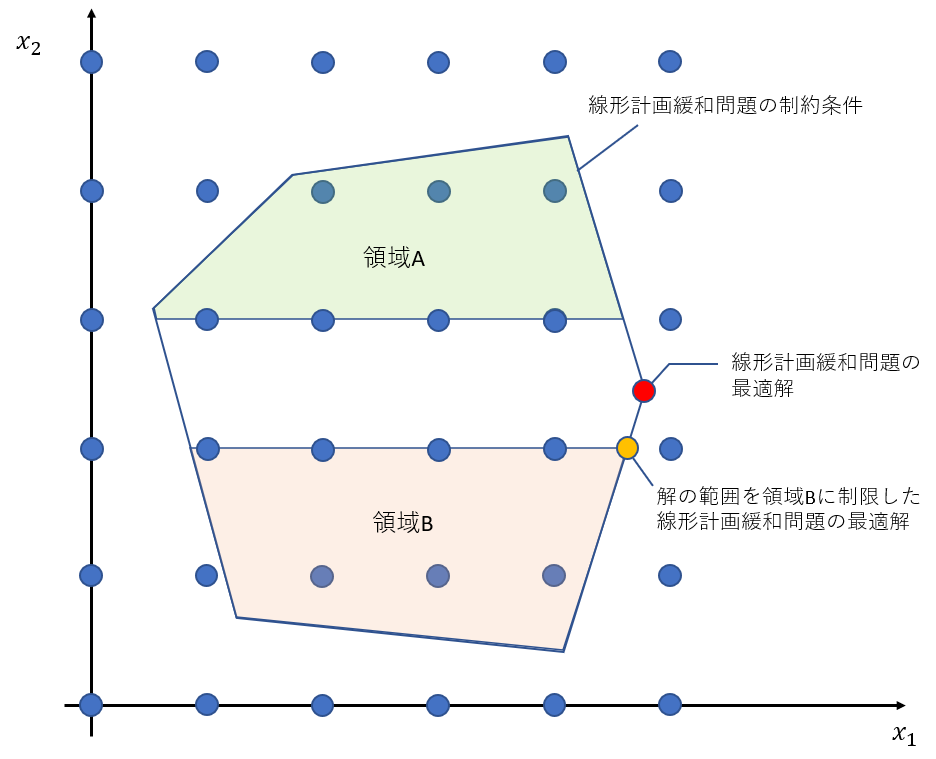
分枝操作では、1つの変数の範囲を制限した小規模な問題をつくります。例えば図2のように、線形計画緩和問題の最適解をもとに、解が領域Aに含まれるという条件を持つ問題と、解が領域Bに含まれるという条件を持つ問題をつくります。分枝操作(すなわち、解の探索範囲の制限)は再帰的に適用でき、新たにつくられた問題は再最適化 (reoptimization) と呼ばれる手続きで効率的に解くことができます。
限定操作では、以下の性質を利用して、最適解が得られる見込みのない問題、すなわち探索が不要な範囲を見つけます。
整数計画問題の暫定的な解を $\boldsymbol{x^\sharp}$ 、新たにつくられた探索範囲の狭い問題 $P$ の線形計画緩和問題 $\bar{P}$ の最適解を $\boldsymbol{\bar{x}}$ とする。それぞれの解の評価値が
f(\boldsymbol{\bar{x}}) \leq f(\boldsymbol{x}^\sharp)を満たす場合、問題 $P$ は $\boldsymbol{x^\sharp}$ より良い解を持たない。
具体的な手続きとしては、新たにつくられた問題の線形計画緩和問題の解を求め、その評価値が暫定的な解の評価値より大きく、かつ整数解である場合は、暫定的な解を更新します。評価値が暫定的な解の評価値より大きいものの整数解でない場合は、さらに分枝操作により新たな問題をつくっていきます。これにより、無駄な探索を省きつつより良い解を見つけることができます。
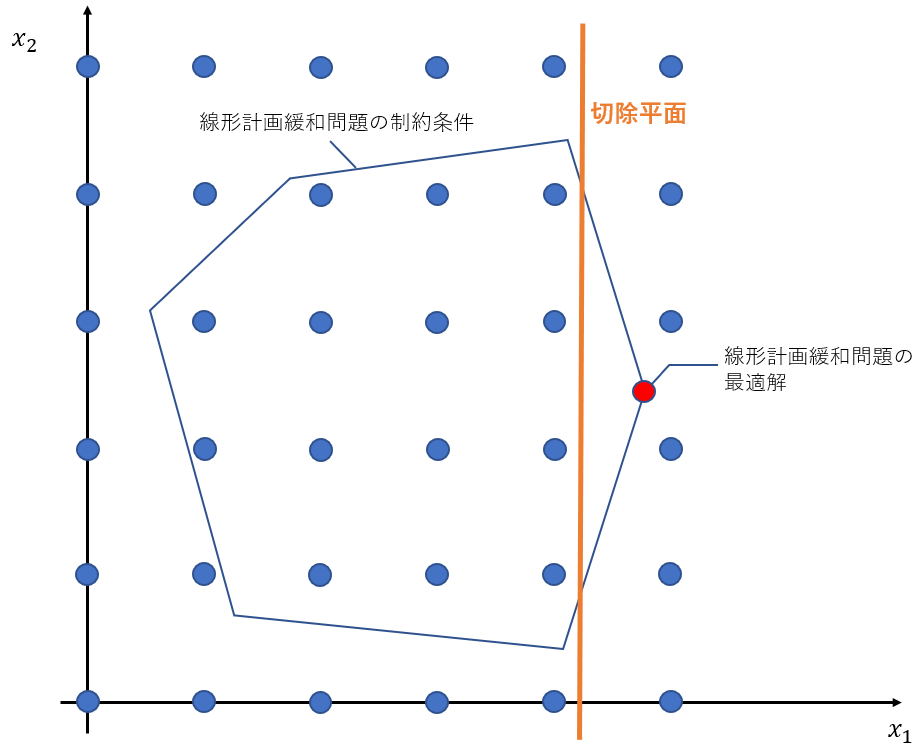
次に、切除平面法について説明します。切除平面法は、整数計画問題の解(つまり、整数解)を残しつつ新たな制約条件を追加することで、解の探索範囲を限定する手法です。線形計画緩和問題の最適解からはじめて、整数解を残しつつ緩和問題の最適解を除去する制約条件を追加する手続きを繰り返し適用していきます。整数計画問題の解を除かない制約条件(妥当不等式と呼ばれます)の中で、緩和問題の解を除くものを切除平面と呼びます。例えば図3のように、整数解(青丸)を残したまま、緩和問題の解(赤丸)のみを除くような切除平面を追加することで、解の探索範囲を狭めていきます。
分枝カット法では、分枝限定法に切除平面法を導入することで、分枝操作で得た問題から得られる最適解を改善し、計算を効率化しています。
3-1-2. 動的計画法
動的計画法 (DP: Dynamic Programming) は、数理最適化問題を小さな部分問題に分割し、各部分問題を解いて得られた最適解を記憶しておくことで、元の問題の最適解を効率よく求める手法です。動的計画法は、「元の問題の最適解が、それを分割した部分問題の最適解を含む」という部分問題最適性(最適性の原理とも呼ばれます)を持つ問題に適用することができます。各部分問題の最適解を保存しておくことで、次の部分問題の最適化でそれ以前に解いた部分問題を改めて解かずに済みます。動的計画法は、ナップサック問題や最短経路問題にも適用できます(ナップサック問題と最短経路問題についての説明は次節を参照)。
3-2. 近似解法
代表的な近似解法である貪欲法を紹介します。また、近似解法のうち、汎用性が高く多くの数理最適化問題に適用できるアルゴリズムの総称をメタヒューリスティクスと呼びます。その中でも、焼きなまし法、遺伝的アルゴリズムを簡単にご紹介します。
3-2-1. 貪欲法
貪欲法 (greedy method) は、段階的に解を求めていく際に、その時点で最も目的関数の評価値が高い解を選ぶことで効率的に解を求める手法です。適用例としては、以下のようなものがあります。
-
ナップサック問題
- 問題設定
- 容量が決まっているナップサックと複数種類の商品があり、ナップサックの容量を超えない範囲で商品をナップサックに詰め、詰めた商品の価値の総和を最大にする商品の組み合わせを求めたい
- 貪欲法による解法
- 容量1単位あたりの価値が高い商品から順に詰めていき、詰められなくなったら打ち切る
- 問題設定
-
最短経路問題
- 問題設定
- 始点からいくつかの地点を経由して終点まで到達する経路のうち、最短の経路を求めたい
- 貪欲法による解法
- 始点からスタートし、現在地と隣り合う地点の中で最も近い地点を順番に選択していく
- 問題設定
貪欲法を使用した場合、厳密に最適解が求まる保証はありませんが、実装が比較的容易で、決定変数の数が多い大規模な問題でも計算時間が比較的短いというメリットがあります。
3-2-2. 焼きなまし法
焼きなまし法 (SA: Simulated Annealing) は、現在得られている暫定的な解の近傍をランダムに探索することで、より良い解を求める手法です。
暫定的な解の近傍において目的関数の評価値が良い解が見つかった場合に移動するだけでなく、評価値が悪化した場合でもある確率で移動することで、局所最適解から脱出し、より良い解を探索します。一定回数の探索を行うか、もしくは暫定的な解の更新頻度が一定値以下になった時点で解の探索を終了することが多いです。ランダムに探索した近傍の評価値が悪化した場合の移動確率は、評価値の変化量と、温度と呼ばれるパラメータによって決定します。探索開始時は移動しやすく、探索が進むにつれ徐々に移動しにくくなるようにすることで、局所最適解から抜け出し、大域的な最適解を見つけやすくしています。
3-2-3. 遺伝的アルゴリズム
遺伝的アルゴリズム (GA: Genetic Algorithm) は、生物の進化に着想を得て解を探索するアルゴリズムです。
複数の解の候補を集合として保持し、交叉や突然変異と呼ばれる操作により新しい解の候補を生成し、選択と呼ばれる操作により次世代の解の候補の集団を決定する手続きを繰り返し、最終的に最も評価値が高い解を選びます。
遺伝的アルゴリズムに登場する操作の説明は以下の通りです。
- 交叉 (crossover)
- 2つ以上の解を組み合わせて新しい解の候補を生成する操作
- 突然変異 (mutation)
- 1つの解の一部をランダムに変化させて新しい解の候補を生成する操作
- 選択 (selection)
- 解の候補の評価値などをもとに、一定数の解の候補を次世代の集団として保持する操作
詳細は割愛しますが、それぞれの操作には設定すべきパラメータが多くあります。解がうまく求まらない場合にはパラメータを設定し直すなどの試行錯誤が必要です。
4. 数理最適化導入の手順
本節では、実際の業務において数理最適化を導入する際の一般的な手順をご紹介します。実際に解決したい問題を数理最適化問題として解く場合、1. 問題の定式化 → 2. 実装 → 3. 分析・検証 → 4. 修正 のサイクルを何度か繰り返し実施します。以下で各ステップについてご説明します。
-
1. 問題の定式化
まず、実際に解決したい問題を数式を使って表現します。2‐2.でご紹介したように、何を最適化(最大化 or 最小化)したいかを表す目的関数、最適化によって値を決める決定変数、満たすべき制約条件を数式で書き表します。問題をどのように定式化すべきかを一から独力で検討するのはなかなか大変ですし、効率良く解ける定式化が知られている場合もありますので、まずは似たような事例がないか書籍やwebで調べてみることがお勧めです。例えば文献[1]には様々なタイプの数理最適化問題とそれに対する解法が紹介されています。
また、以降のステップで、定式化した問題を解くことが難しい(例:ソルバーによっては非線形問題は解けない)ことが判明した場合には、定式化の工夫(例:非線形から線形への変換など)や近似解法への切り替えなどの検討などが必要です。 -
2. 実装
次に、数理最適化ソルバーのメソッドを利用し、定式化した問題を記述します。数理最適化ソルバーには、商用/非商用のものがあります。非商用の数理最適化ソルバーとしては、例えば PuLP や Python MIP があります。いずれもオープンソース開発のコミュニティCOIN ORからダウンロードできます。 -
3. 分析・検証
定式化した問題のコーディングが完了したら、まずは簡単な問題例に対して想定通りの最適解が得られるかを確認することをお勧めします。実際に解決したい問題よりも決定変数の数を減らした、手計算で解を求められる程度の問題例を作成し、その最適解が制約条件を全て満たしているかを確認します。これにより、明らかに意図通りでない問題設定や実装になっていないかをチェックすることができます。
適切に実装できていれば、実際に解決したい問題に対して数理最適化ソルバーを実行します。実行後、得られた解が制約条件を満たしているか、実行時間が許容範囲内かを確認します。定式化にミスがある場合、制約条件を満たす解が存在せず実行不能と出力されることがあります。この場合、制約条件どうしが矛盾していないか等を見直す必要があります。 -
4. 修正
ここまでで、得られた解の精度や実行時間について課題がある場合は、定式化やコードの修正作業を行います。
同じ問題を数理最適化ソルバーで解いた場合と近似解法で解いた場合で、得られる解の精度と実行時間にどの程度差があるかという視点は、最適化の方針を決定する上で重要です。また、数理最適化問題の実装においては、想定されるパターンを考慮した様々な問題例について解を求め、得られた解が想定通りかを地道に確認することが重要です。
5. まとめ
ここまで、数理最適化の基本的な事項についてご紹介しました。数理最適化は応用範囲が広く、ビジネスの現場での問題解決に大きく役立つ技術だと思います。本記事が数理最適化を活用したいという方の一助になれば幸いです。
6. 参考文献
- 久保幹雄・J.P.ペドロソ・村松正和・A.レイス 『あたらしい数理最適化 Python言語とGurobiで解く』近代科学社
- 金谷健一『これなら分かる最適化数学 基礎原理から計算手法まで』共立出版
- 梅谷俊治『組合せ最適化問題に対する実用的なアルゴリズムとその応用』
- 京都大学大学院情報学研究科 数理工学専攻 離散数理分野紹介資料
- 梅谷俊治『しっかり学ぶ数理最適化 モデルからアルゴリズムまで』講談社
-
組み合わせ最適化問題 (combinational optimization problem) と呼ばれることもあります。 ↩