回帰分析におけるパラメータ推定：最尤法と最小二乗法

1. はじめに

最近、ロジスティック回帰や指数回帰、べき乗回帰におけるパラメータ推定方法について勉強したのでまとめてみました。回帰分析について基礎的な知識はあるが、パラメータ推定の理論的裏付けについて知りたい方向けの記事になります。

まず、線形回帰における最小二乗法と最尤法について整理し、それらの手法で同様のパラメータ推定ができる条件を確認します。次に、ロジスティック回帰や指数回帰、べき乗回帰におけるパラメータ推定方法を説明します。

2. 線形回帰におけるパラメータ推定

2-1. 最小二乗法

線形回帰は、2変数 $X, Y$ の間に $Y=aX+b$ の関係があると仮定して回帰分析を行う手法です¹。すべてのデータ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ に対して $y_i=ax_i+b$ を満たすような $a, b$ はふつう存在しないので、$X$ と $Y$ との定量的な構造（モデル）をもっとも良く表現できる最適なパラメータ $a, b$ を選ぶ必要があります。$a, b$ を推定するのによく使われる方法が最小二乗法です。最小二乗法は、残差 $e_i=y_i-(ax_i+b)$ の平方和

\sum_{i=1}^n e_i^2 = \sum_{i=1}^n \{y_i-(ax_i+b)\}^2 \tag{1}

を最小にするような $\hat{a}, \hat{b}$ を $a,b$ の推定量とします。残差は、$Y$ が $X$ で説明できない部分を表しており、この総和が小さい方が望ましいという考え方です。

2-2. 最尤法

最尤法（最尤推定法とも呼ばれます）は、「実際に得られたデータは、得られる確率が最大のものが得られている」という仮定にもとづき、最適なパラメータを推定する方法です。パラメータ $\theta$ と、そのパラメータのもとでデータ $z_i$ が得られる確率 $f(z_i|\theta)$ を考えたとき、尤度関数

L(\theta)=\prod_if(z_i|\theta)

を最大化するようにパラメータ $\theta$ を推定します。尤度関数は積の形をしており、数学的に扱うには不便であるため、尤度関数と単調な関係にある対数尤度関数

\log L(\theta)=\log\prod_if(z_i|\theta)=\sum_i\log f(z_i|\theta)

を扱うことが多いです。

2-3. 線形回帰における最小二乗法と最尤法の関係

2-1.で触れたデータ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ について、正規線形モデル

y_i=ax_i+b+\epsilon_i

を考えます。誤差項 $\epsilon_i$ は互いに独立に正規分布 $N(0,\sigma^2)$ にしたがうとします。

尤度関数は

L(a, b) = \prod_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} \exp\left[-\frac{\{y_i-(ax_i+b)\}^2}{2\sigma^2}\right]

と表され、対数尤度関数は

\log L(a, b)=-\frac1{2\sigma^2}\sum_{i=1}^n \{y_i-(ax_i+b)\}^2-\frac{n}{2}\log(2\pi\sigma^2) \tag{2}

と表されます。最尤法によるパラメータ推定では、対数尤度関数を最大化することを考えますが、パラメータ $a, b$ に依存しているのは式(2)の第一項のみであるため、第一項を最大化することを考えればよいです。この第一項に着目すると、最小二乗法で最小化したい残差平方和（式(1)）と同様の数式になっていることがわかります。つまり、

線形回帰における誤差項が正規分布にしたがうことを仮定してパラメータを推定すると、最尤法と最小二乗法は同一の推定量を与えます。

3. ロジスティック回帰におけるパラメータ推定

3-1. 最尤法によるパラメータ推定

ロジスティック回帰は、目的変数が2値変数であるデータ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ （ただし、$y_i\in\{0,1\}$）において、目的変数 $y_i$ の生起確率 $\pi_i$ が

\pi_i = P(y_i=1|a,b) = \frac1{1+e^{-(ax_i+b)}}

という関係になっていると仮定して回帰分析を行う手法です。

ロジスティック回帰では最尤法でパラメータを推定します。いま、データ $y_1, y_2, \cdots, y_n$ は互いに独立にベルヌーイ分布 $Be(\pi_i)$ にしたがうと仮定しているため、データ $(x_i, y_i)$ に対する尤度関数は

\begin{cases}
\pi_i&(y_i=1)\\
1-\pi_i&(y_i=0)
\end{cases}

と表現でき、$y_i=1$ の場合と $y_i=0$ の場合をまとめると

\pi_i^{y_i}(1-\pi_i)^{1-y_i}

と書くことができます。すべてのデータ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ に対する尤度関数は

\prod_{i=1}^n \pi_i^{y_i}(1-\pi_i)^{1-y_i}

となり、対数尤度関数は

\log \biggl( \prod_{i=1}^n \pi_i^{y_i}(1-\pi_i)^{1-y_i} \biggr) = \sum_{i=1}^n \biggl( y_i \log \pi_i + (1-y_i) \log (1-\pi_i) \biggr) \tag{3}

となります。最尤法では式(3)を最大化するパラメータを求めますが、これは解析的には解くことができないため、数値計算を利用してパラメータを求めます。

3-2. 最小二乗法でパラメータ推定すると？

線形回帰の場合と同様に、最小二乗法でパラメータ推定することを考えます。最小二乗法は、残差 $e_i=y_i-\pi_i$の平方和

\sum_{i=1}^n (y_i-\pi_i)^2=\sum_{i=1}^n \left(y_i-\frac1{1+e^{-(ax_i+b)}}\right)^2 \tag{4}

を最小にするようなパラメータ $a, b$ を求める方法でした。式(3)と式(4)を見比べてみると、まったく違う数式であることがわかると思います。つまり、これらを解いて得られるパラメータの値も異なってしまいます。

なぜロジスティック回帰では最尤法と最小二乗法で得られる結果が異なってしまうのでしょうか？それはデータに関する仮定が異なるためです。2.では、線形回帰における誤差項が正規分布にしたがうとき、最尤法と最小二乗法で得られるパラメータの推定値が同じになることを見ましたが、いま考えているのは $y_i\in\{0,1\}$ であり、残差 $e_i = y_i-\pi_i$ が正規分布にしたがうと仮定することは適切ではないでしょう。
$\pi_i = \frac1{1+e^{-(ax_i+b)}}$ を式変形して得られる $q_i = \log \frac{\pi_i}{1-\pi_i} = ax_i+b$ についての残差 $e_i = q_i - (ax_i+b)$ も、やはり正規分布にしたがうと仮定することは適切でなく、最尤法と最小二乗法で得られる結果は異なるものになるでしょう。

実際に扱うデータを調査したうえで、データに関する妥当な仮定をおき、適切なパラメータ推定方法を選択することが重要です。目的変数が2値変数でありロジスティック回帰モデルを仮定する際は、最小二乗法ではなく最尤法を用いてパラメータを推定します。

4. その他の回帰分析におけるパラメータ推定

この章では、指数回帰やべき乗回帰におけるパラメータ推定について考えます。

4-1. 指数回帰におけるパラメータ推定

指数回帰は、2変数 $X, Y$ の間に $Y=e^{aX+b}$ の関係があると仮定して回帰分析を行う手法です。線形回帰の場合と同様に最小二乗法でパラメータ $a, b$ を推定することを考えます。ここでは、データ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ に対して、残差平方和

\sum_{i=1}^n (y_i-e^{ax_i+b})^2

を最小にする方法と、$Y=e^{aX+b}$ の両辺の対数をとったうえでの残差平方和

\sum_{i=1}^n \{\log y_i-(ax_i+b)\}^2

を最小にする方法の2つを比較してみましょう。一般にこの二つの方法は同じ結果を与えませんが、どちらが適切な方法なのでしょうか？
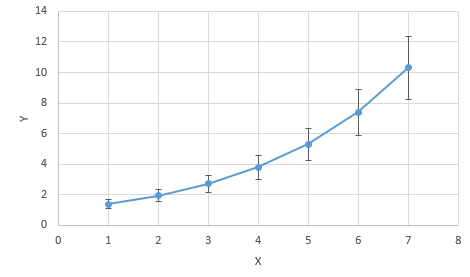
正解は、後者の両辺の対数をとってから残差平方和を最小にする方法です。というのも、指数回帰で分析を行う際は、実際に扱うデータ $(x_1, y_1), (x_2,y_2), \cdots, (x_n, y_n)$ がおおむね $y_i>0, e^{ax_i+b}>0$ を満たしていることが想定され、前者の方法の残差が、一定のばらつきを持つ正規分布にしたがうと仮定することは適切でないためです。例えば、ある程度データにフィットした指数曲線を描いてみると、$y_i$が小さいほど残差（つまり、指数曲線とデータのずれ）も小さく、反対に $y_i$ が大きいほど残差も大きくなる傾向があるイメージが持てると思います（図１）。最小二乗法では、どのデータも平等にその残差の2乗を小さくするようなパラメータを求めるため、$y_i$ が大きなデータをより重視する形となってしまいます。一方、後者の方法の場合、$\log y_i=ax_i+b$ は実数全体に分布し、その残差が一定のばらつきを持つ正規分布にしたがうと仮定することは（前者の方法よりも）妥当だと考えられます。よって、指数回帰においては後者の、両辺の対数をとってから最小二乗法を適用する方が適切であるといえます。副次的なメリットとして、後者の方法の場合は残差平方和がパラメータ $a, b$ の二次関数で表現されるため、解析的に解を求めることができる点が挙げられます。

          図１：指数回帰のイメージ

4-2. べき乗回帰におけるパラメータ推定

べき乗回帰は、2変数 $X, Y$ の間に $Y=aX^b$ の関係があると仮定して回帰分析を行う手法です。この場合も指数回帰の場合と同様に、最小二乗法でパラメータ $a, b$ を推定することを考えます。一つはそのままの残差平方和

\sum_{i=1}^n (y_i-ax_i^b)^2

を最小にする方法、もう一つは $Y=aX^b$ の両辺の対数をとった残差平方和

\sum_{i=1}^n \{\log y_i-(\log a+b\log x_i)\}^2

を最小にする方法です。指数回帰の場合と同様に、この場合も後者の両辺の対数をとってから最小二乗法を用いる方が適切でしょう。べき乗回帰で分析を行う場合、実際に扱うデータはおおむね $y_i>0,ax_i^b>0$ を満たしていると想定されるため、前者の方法では残差が一定のばらつきを持つ正規分布にしたがうと仮定することは適切でないと考えられる一方で、後者の方法ならば $\log y_i=\log a+b\log x_i$ が実数全体に分布し、その残差が一定のばらつきを持つ正規分布にしたがうと仮定することは（前者の方法よりも）妥当と考えられるためです。べき乗回帰の場合も、副次的なメリットとして、後者の方法なら解析的にパラメータを求められるという点が挙げられます。

指数回帰・べき乗回帰ともに、そのまま最小二乗法を適用するのではなく、両辺の対数をとってから最小二乗法を適用することでパラメータ推定する方が適切です。

5. まとめ

この記事では、線形回帰やロジスティック回帰、指数回帰、べき乗回帰におけるパラメータ推定方法をまとめました。この記事で紹介しきれなかった回帰分析においても、「最小二乗法が適用できるのは残差が正規分布にしたがうときである」という事実を思い起こせば、どのようにパラメータを推定すべきか判断できるでしょう。回帰分析の理論的側面に興味がある方の理解の助けになれば幸いです。

6. 参考文献

1. 東京大学教養学部統計学教室 編『統計学入門』東京大学出版会
2. 東京大学教養学部統計学教室 編『自然科学の統計学』東京大学出版会
3. ロジスティック回帰と最尤推定法
4. 最小二乗法と最尤法
5. 最尤推定
6. 指数関数でフィッティングしても残差平方和が最小にならない（後編）

1. ここでは簡単のため、説明変数が1個である単回帰について説明しています。 ↩