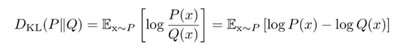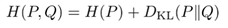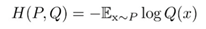線形代数
固有値と固有ベクトル
ある行列Aに対する特殊なベクトル「x」と右辺の係数「λ」において、「Ax = λx」が成立する場合、「x」を行列Aに対する固有ベクトル、λを固有値という。固有値ベクトルは、Ax = λx ⇒「 (A-λI)x = 0, x ≠ 0」より|A-λI| = 0 を解くことで求められる。
固有値分解
ある実数を正方形に並べて作られた行列Aが固有値「λ1,λ2・・・」と固有ベクトル「v1, v2・・・」を持った時、この固有値を対角線上に並べた行列（それ以外の成分は0）「𝛬」とそれに対応する固有ベクトルを並べた行列「V」を用意したとき、それらは「AV = V𝛬」となる。
したがって「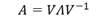
」と変形できる。
このように正方形の行列を上述のような３つの行列の積に変換することを固有値分解という。
（これにより、行列の累乗計算が容易になる。）
特異点分解
正方行列以外の行列に対する固有値分解（に似たもの）で、
Mv=𝜎u・Mu=𝜎vの場合に、「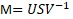
」として特異点分解することができる。
また、「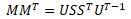
」を固有値分解することでその左特異ベクトルと特異値の２乗を求めることができる。
確率統計
確率の種類
・頻度確率（客観確率） ⇒ 発生する頻度
・ベイズ確率（主格確率） ⇒ 信念の度合い
条件付き確率と独立した事象の同時確率
・条件付き確率
ある事象X=xが与えられた下で、Y=yとなる確率
P(Y=y|X=x) = P(X=x)P(Y=y)/P(X=x)
・独立した事象の同時確率
事象X=xと事象Y=y（XとYに因果関係はない）が同時に発生する確率
P(X=x,Y=y)=P(X=x)P(Y=y)=P(Y=y,X=x)
ベイズ則
・事象X=xと事象Y=yについて以下が成り立つ
P(X=x|Y=y)P(Y=y) = P(Y=y|X=x)P(X=x)
確率変数と確率分布
・確率変数
事象と結びつけられた数値
・確率分布
事象の発生する確率の分布
・期待値
その分布における確率変数の平均値（ありえそうな値）
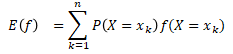
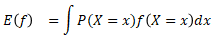※連続値の場合
分散と共分散
・分散
データの散らばり具合（期待値からのズレを平均したもの）
・共分散
２つのデータ系列の傾向の違い
正の値：似た傾向、負の値：異なる傾向、ゼロ：関係性に乏しい
様々な確率分布
・ベルヌーイ分布（２択（表裏など）で成立）
・マルチヌーイ（カテゴリカル）分布（複数選択（さいころのような）で成立）
・二項分布（ベルヌーイ分布の多試行版）
・ガウス分布（釣鐘型の連続分布）
情報理論
自己情報量
以下の式で表される
I(ｋ) = -log(P(x)) = log(W(x))
シャノンエントロピー
自己情報量の期待値
H(x) = -Σ(P(x)log(P(x)))
カルバック・ライブラー（KL） ダイバージェンス
同じ事象・確率変数における異なる確率分布P,Qの違い
交差エントロピー
KLダイバージェンスの一部分を取り出したもの
⇒ Qについての事故情報量をPの分布で平均
