はじめに
ビジネスにおいて予測モデルを作成する際,ユーザにとっての解釈しやすさを優先して,線形モデルや決定木のような比較的単純なモデルを使わざるを得ないという場合は結構多いのではないだろうか.
しかし,せっかくデータ分析業をやっている身としては,仕事でももっと色々なモデルを活用したいというのが人情であろう.まあそういう個人的欲求は置いておくにしても,単純なモデルを使う際に気を付けないといけない事柄というのが色々ある.
-
説明変数と目的変数の関係は線形か?
-
予測に効くのはどの変数か?
-
変数間の交互作用を見逃していないか?
等々.
さて,ここで複雑なモデルであれば非線形性や交互作用も自動的に取り入れてくれるのになあ,と思ったところで発想を転換してみたい.つまり,最終的な予測モデルは単純なものを使うとしても,上記のような問題を検討するための探索的データ分析の段階で,より複雑なモデルを活用できるのではなかろうか.
というわけで以下のパッケージを紹介したい.
名前の通り,ランダムフォレストで探索的データ分析しようぜ,というパッケージだ.
ランダムフォレスト系のパッケージ(randomForest, randomForestSRC, ranger, party)に対して,統一的なインターフェイスで
- 部分従属プロット(partial dependency plot)
- 変数重要度(variable importance)
- データ点の間の類似度(proximity)
の計算と描画ができるようになっている.3つともすでによく知られた事柄かもしれないが,探索的データ分析のための道具として捉えようというのは結構おもしろいと思う.
部分従属プロット
モデルの予測値が,ひとつの説明変数に対して平均的にはどのように依存しているのかを描いたものが部分従属プロットだ.説明変数と目的変数の間に非線形な関係がないかチェックするのに使うことができる.
edarf ではpartial_dependence()関数で,部分従属性を計算したデータフレームを作成する.
library(edarf)
library(randomForest)
fit <- randomForest(Species ~ ., iris)
pd <- partial_dependence(fit, data = iris, vars = "Petal.Width")
head(pd)
## setosa versicolor virginica Petal.Width
## 1 0.6476933 0.2322133 0.1200933 0.1000000
## 2 0.6476933 0.2322133 0.1200933 0.2142857
## 3 0.6476933 0.2322133 0.1200933 0.3285714
## 4 0.6476933 0.2322133 0.1200933 0.4428571
## 5 0.6476933 0.2322133 0.1200933 0.5571429
## 6 0.6311867 0.2458000 0.1230133 0.6714286
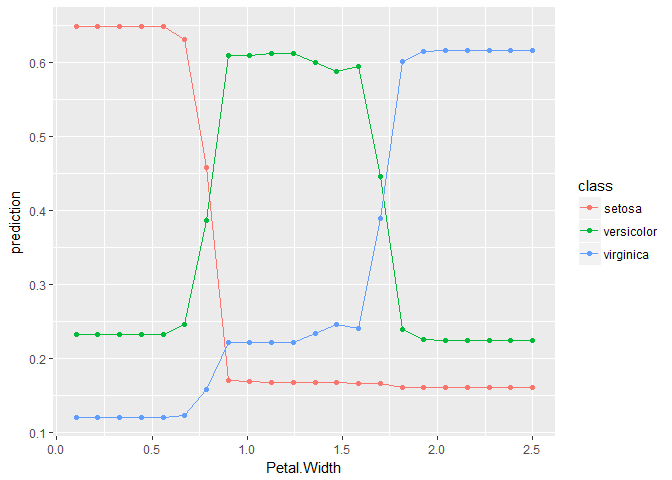
作成したデータフレームをplot_pd()関数に渡せば部分従属プロットが描画される.
plot_pd(pd)
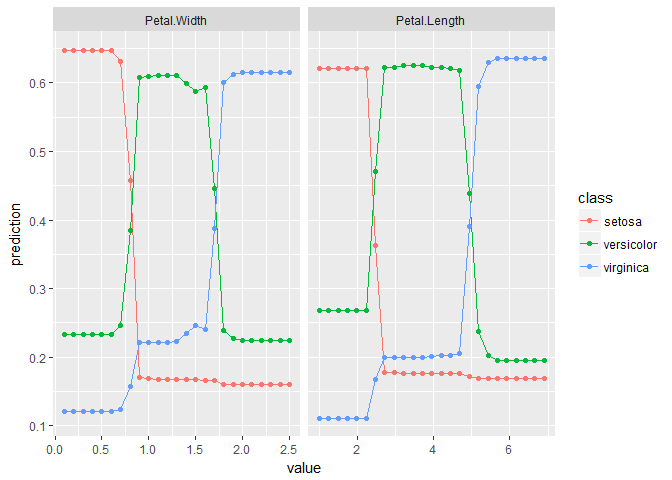
複数の変数に対して,部分従属プロットをまとめて計算することもできる.
pd_list <- partial_dependence(fit, data = iris, vars = c("Petal.Width", "Petal.Length"))
plot_pd(pd_list)
さて,実は元祖randomForestでもrandomForest::partialPlot()関数で部分従属プロットが描けるので,これだけだとedarfのありがたみがちょっと薄いのだが,edarfでは多変数の交互作用を取り入れた部分従属プロットも描くことができる.これを使えば影響の大きい交互作用がないかチェックできる.
交互作用を見るにはpartial_dependence()関数でinteraction=TRUEとすればよい.
pd_int <- partial_dependence(fit, data = iris, vars = c("Petal.Length", "Petal.Width"), interaction = TRUE)
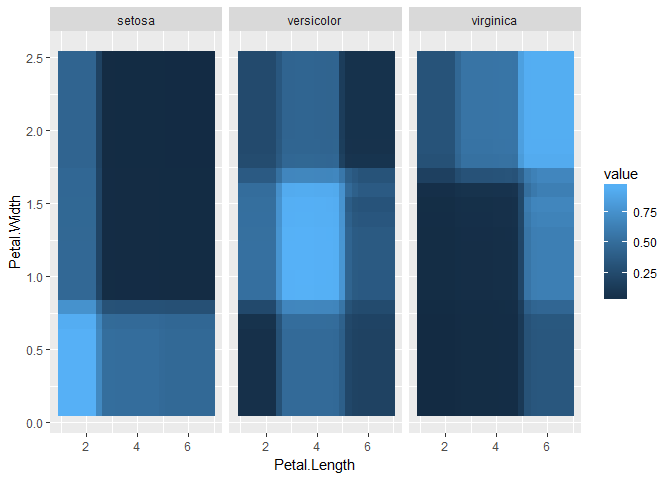
plot_pd(pd_int)
見ての通り,2変数に対する予測値がヒートマップ的に描画される.
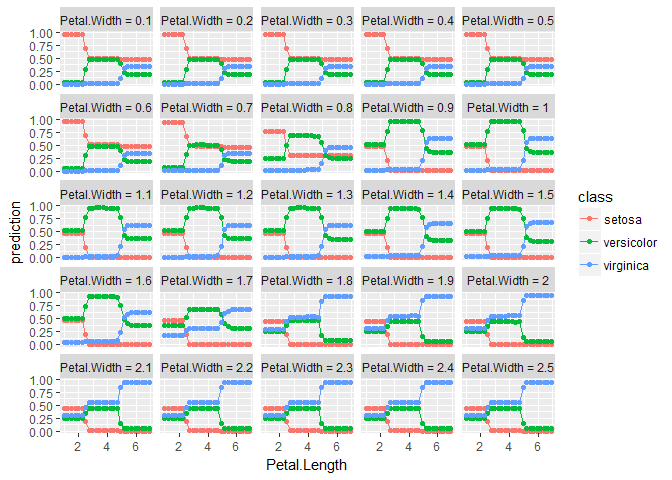
引数でfacetを指定すると,指定した方の変数で層別された折れ線グラフになる.この例ではごちゃごちゃした図になってしまうが,カテゴリカルな説明変数との交互作用が見たい場合はこちらが便利だろう.
plot_pd(pd_int, facet="Petal.Width")
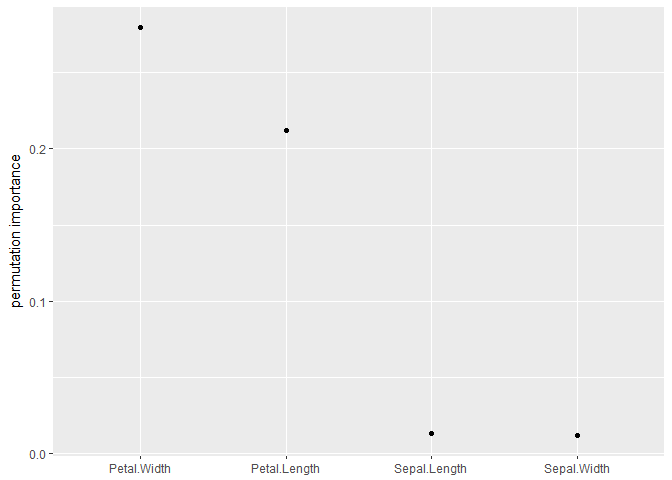
変数重要度
これはおなじみのランダムフォレストによる変数重要度を計算してくれる.変数重要度はどのパッケージでももとから計算可能なので,インターフェイスの統一がメリット.
imp <- variable_importance(fit, data = iris, vars = names(iris)[-5])
plot_imp(imp)
データ点の間の類似度
2つのデータ点に対して,ランダムフォレストの各ツリーにおいて同じ終端ノードに2点が落ちる割合をそのデータ点の間の類似度とする.randomForest, randomForestSRC, partyパッケージではもとから計算できるのだがインターフェイスが異なっており,またrangerではサポートされていないようである.
edarfではextract_proximity()関数で類似度行列を計算できる.
prox <- extract_proximity(fit, newdata = iris)
str(prox)
## num [1:150, 1:150] 1 0.984 0.994 0.99 1 0.998 1 1 0.984 0.99 ...
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:150] "1" "2" "3" "4" ...
## ..$ : chr [1:150] "1" "2" "3" "4" ...
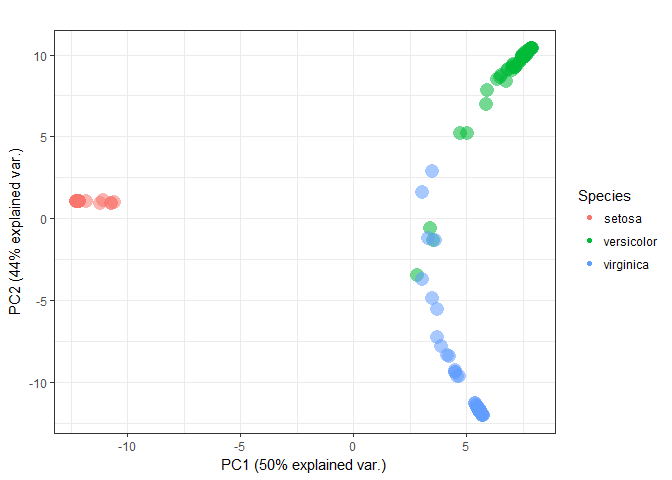
類似度行列は(データ数)x(データ数)の大きさの行列なので,そのままだとよく分からない.そこでedarfでは,類似度行列をstats::prcomp()で主成分分解したオブジェクトをいい感じにプロットしてくれる関数plot_prox()が提供されている.
pca <- prcomp(prox, scale = TRUE)
plot_prox(pca, color = iris$Species, color_label = "Species", size = 2)
関連情報
edarfに似た狙いを持つと思われるパッケージとして,
がある.日本語の解説もある.
また,ランダムフォレストから人間にもわかる知見を得るための別のアプローチとして,ランダムフォレストから重要な予測ルールを抽出するという研究がある.
前者については日本語解説がある.
後者はまだR実装がないようなのが残念だ.
部分従属プロットはランダムフォレストでなくとも,任意のモデルに対して計算することができる.Rの機械学習フレームワークであるmlrパッケージにそのためのメソッドがある.また,部分従属プロットのような平均的な予測値だけでなく,予測値のばらつきも合わせて可視化できるパッケージとしてICEBoxがある.
最近の機械学習業界には複雑なモデルをどう解釈可能にするかという問題関心があるようだ.こういった研究もデータの分析のための道具という観点で見てみるとおもしろいかもしれない.