3Dの基本的な知識を理解したくて、『3次元CGの基礎と応用[新訂版]( http://goo.gl/GKoQ4y )』という書籍を購入しました。薄くて読みやすそうな本なのですがサンプルソースがないので、勉強がてらサンプルを作りながら読み進めようと思います。誰でもすぐに追試ができるよう、HTML + Javascriptでサンプルを作っていきます。
完全なサンプルはこちら
https://github.com/nakaken0629/3dstudy
4.0. フラットシェーティング
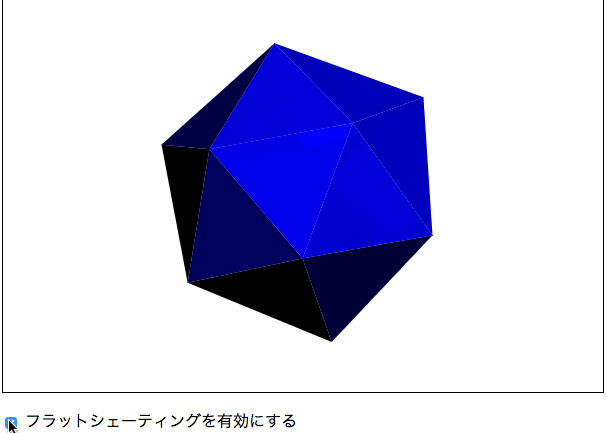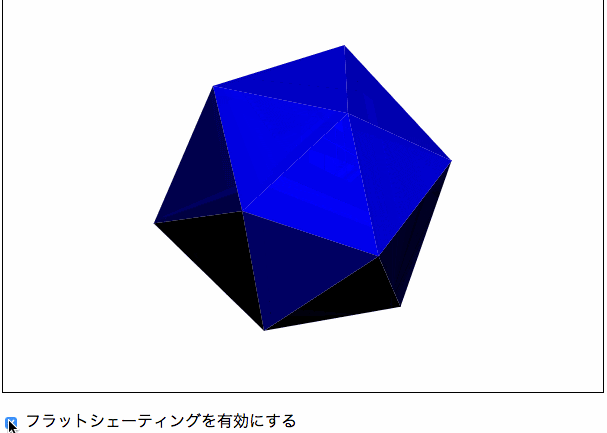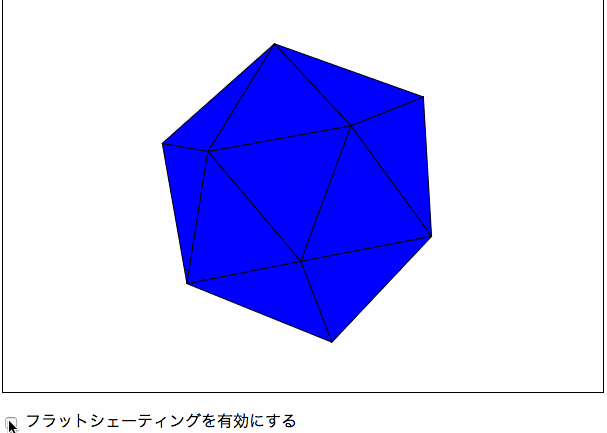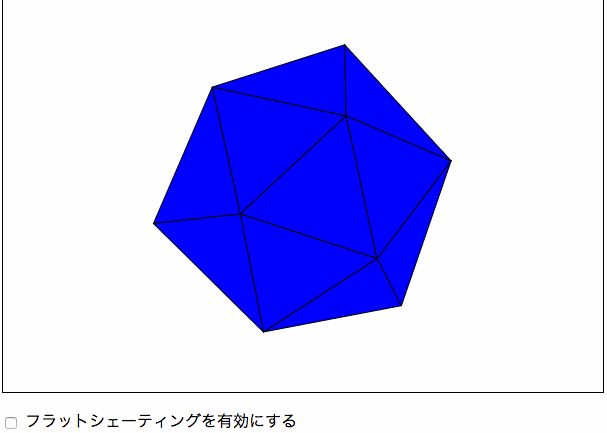
書籍にはありませんが、第4章のスムーズシェーディングを学ぶ前に、スムーズでないシェーディング、すなわちフラットシェーティングについて学ぼうと思い、作成しました。
フラットシェーティングは、ポリゴンの法線と光源の角度によって色が決まります。法線と光源のなす角度が0度(つまり光源がポリゴンに対して垂直にある場合)は、ポリゴンが最も明るく表示され、逆に法線と光源のなす角度が±90度(つまり光源がポリゴンに対して平行にある場合)は、ポリゴンが最も暗く表示されます。これらの範囲外の場合は、ポリゴンの裏面に光が当たっている状態なのでポリゴンは黒色で表示されます。
サンプルソース
var fillTriangle = function(p, light) {
var checked = document.forms[0].enabled.checked
if (checked) {
/* フラットシェーティングあり */
/* ポリゴンの法線ベクトル */
var n = normal(p);
/* 光線。スクリーン座標でいうと、右上の少し手前から照らしている */
var light = {'x': 250.0, 'y': -500.0, 'z': 1000.0, 'r': 255, 'g': 255, 'b': 255}
/* 法線と光線の角度を元に、ポリゴンの見た目の色を計算する */
var rate = (n.x * light.x + n.y * light.y + n.z * light.z)
/ Math.sqrt(Math.pow(n.x, 2) + Math.pow(n.y, 2) + Math.pow(n.z, 2))
/ Math.sqrt(Math.pow(light.x, 2) + Math.pow(light.y, 2) + Math.pow(light.z, 2));
rate = rate > 0 ? rate : 0;
rgb = createRgb(
Math.floor(p.r * light.r / 255.0 * rate),
Math.floor(p.g * light.g / 255.0 * rate),
Math.floor(p.b * light.b / 255.0 * rate)
);
} else {
/* フラットシェーティングなし */
rgb = createRgb(0, 0, 255);
}
/* 以下、ポリゴンを表示するロジック */
}
参考:正二十面体の座標計算
正二十面体の座標は、以下のURLに簡単に求めるアルゴリズムが紹介されている。XY平面、YZ平面、ZX平面に長方形を配置して、それらが中心で交わるようにすると、この長方形の頂点が二十面体の頂点になります。長方形の縦横比を黄金律にすると正二十面体の頂点になります。具体的には次のようになります。
(±1,±G,0)
(0,±1,±G)
(±G,0,±1)
※ Gは黄金比
http://ynomura.dip.jp/archives/2009/08/20.html
http://sci-tech.ksc.kwansei.ac.jp/~shimeno/math/golden/goldensection.html
これらの頂点から構成される全ての三角形(20C3 = (201918)/(321) = 1140通り)について、3辺の長さがすべて最短のものが、正二十面体の各面になります。この組み合わせを探し出すアルゴリズムを、Pythonで作成しました。
rom numpy import *
from math import *
import itertools
g = (1.0 + sqrt(5)) / 2.0
v = []
v.append(array([+1.0, +g , 0.0, 0.0]))
v.append(array([-1.0, +g , 0.0, 0.0]))
v.append(array([+1.0, -g , 0.0, 0.0]))
v.append(array([-1.0, -g , 0.0, 0.0]))
v.append(array([ 0.0, +1.0, +g, 0.0]))
v.append(array([ 0.0, -1.0, +g, 0.0]))
v.append(array([ 0.0, +1.0, -g, 0.0]))
v.append(array([ 0.0, -1.0, -g, 0.0]))
v.append(array([ +g, 0.0, +1.0, 0.0]))
v.append(array([ -g, 0.0, +1.0, 0.0]))
v.append(array([ +g, 0.0, -1.0, 0.0]))
v.append(array([ -g, 0.0, -1.0, 0.0]))
rs = array([
[ 1000, 0, 0, 0],
[ 0, 1000, 0, 0],
[ 0, 0, 1000, 0],
])
for vv in v:
vv = dot(vv, rs)
print(vv)
for element in itertools.combinations(xrange(len(v)), 3):
v0 = v[element[0]]
v1 = v[element[1]]
v2 = v[element[2]]
n0 = linalg.norm(v0 - v1)
n1 = linalg.norm(v1 - v2)
n2 = linalg.norm(v2 - v0)
if n0 == 2.0 and n1 == 2.0 and n2 == 2.0:
print(element, n0, n1, n2)
これを実行すると、次の結果が表示されます。
$ python session4_0.py
[ 1000. 1618.03398875 0. 0. ]
[-1000. 1618.03398875 0. 0. ]
[ 1000. -1618.03398875 0. 0. ]
[-1000. -1618.03398875 0. 0. ]
[ 0. 1000. 1618.03398875 0. ]
[ 0. -1000. 1618.03398875 0. ]
[ 0. 1000. -1618.03398875 0. ]
[ 0. -1000. -1618.03398875 0. ]
[ 1618.03398875 0. 1000. 0. ]
[-1618.03398875 0. 1000. 0. ]
[ 1618.03398875 0. -1000. 0. ]
[-1618.03398875 0. -1000. 0. ]
((0, 1, 4), 2.0, 2.0, 2.0)
((0, 1, 6), 2.0, 2.0, 2.0)
((0, 4, 8), 2.0, 2.0, 2.0)
((0, 6, 10), 2.0, 2.0, 2.0)
((0, 8, 10), 2.0, 2.0, 2.0)
((1, 4, 9), 2.0, 2.0, 2.0)
((1, 6, 11), 2.0, 2.0, 2.0)
((1, 9, 11), 2.0, 2.0, 2.0)
((2, 3, 5), 2.0, 2.0, 2.0)
((2, 3, 7), 2.0, 2.0, 2.0)
((2, 5, 8), 2.0, 2.0, 2.0)
((2, 7, 10), 2.0, 2.0, 2.0)
((2, 8, 10), 2.0, 2.0, 2.0)
((3, 5, 9), 2.0, 2.0, 2.0)
((3, 7, 11), 2.0, 2.0, 2.0)
((3, 9, 11), 2.0, 2.0, 2.0)
((4, 5, 8), 2.0, 2.0, 2.0)
((4, 5, 9), 2.0, 2.0, 2.0)
((6, 7, 10), 2.0, 2.0, 2.0)
((6, 7, 11), 2.0, 2.0, 2.0)